RADIOAKTÍV SUGÁRZÁS JELLEMZŐI
A mérés elkészítésének több célja is volt. Az első, hogy megismerjük az egyik lehető legegyszerűbb áramkört, amellyel radioaktív sugárzást tudjuk detektálni. A második cél, hogy ezen áramkör részegységeit (oszcillátor, sokszorozó, Geiger-Müller cső), ha nem is teljes részletességgel, de valamennyire bemutassuk. A harmadik, hogy az időben véletlenszerű (statisztikus) jelek törvényszerűségeit, és minimális feldolgozási módszereit legalább bevezető szinten megismerjük.
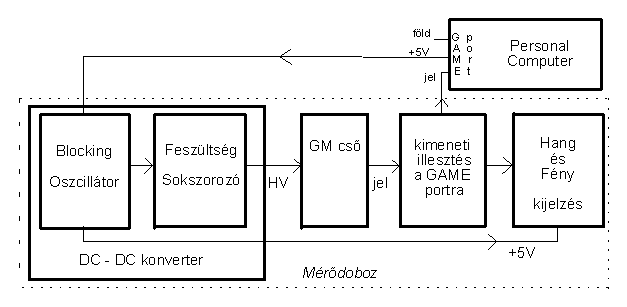
A mérési összeállítás (1.ábra.) egyes egységei:

1. ábra.
a./ Egy PC, amelynek a játék (game) portját két célra használjuk fel. Egyrészt ez szolgáltatja a +5 voltos tápfeszültséget, és a föld csatlakozást, másrészt ide adjuk be a detektorból kijövő, - illes
ztési okból kissé formált - statisztikus jeleket.b./ Mérődoboz, amely tartalmazza a DC/DC konvertert, és a PC-hez illesztő áramkört. A konverter 5 voltból állítja elő a Geiger-Müller (szokásos rövidítéssel: GM) cső működéséhez szükséges néhány száz volto
s nagyfeszültséget (High Voltage :HV).A GM cső képes a megfelelő típusú és energiájú radioaktív sugárzásból elektromos impulzusokat előállítani. Ennek a közelébe, egy megfelelően kialakított tartóba, helyezzük a radioaktív izotópot, amely esetünkben gamm
a sugarakat bocsát ki.A detektor és a sugárforrás egymáshoz képest elmozdíthatóak. Az elmozdítás mértéke, egy rögzített centiméter skálán, leolvasható.
A kijelző egység, amely optikailag és akusztikusan is jelzi a radioaktív sugárzás aktuális erősségét
(intenzitását).
Ismerkedjünk meg a mérődobozban található áramkörökkel.
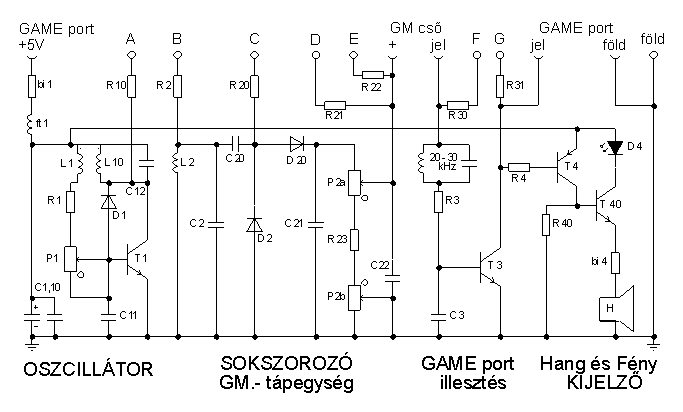
2.ábra.
Alkatrészlista:
Oszcillátor: R1=1k, R10=10k, P1=22k, ft1=fojtó, bi1=biztosíték 0,1A.
C1=10m , C10=47n, C11=100p, C12=68p.
D1=Si dióda, T1=BC301, L1=L10=20menet, L2=800menet mindhárom csatolt.
Sokszorozó: R2=R20= R22=10M, R21=10G, R23=2M, P2=2x2.2M.
C2=100p, C20=C21=C22=330n / legalább 630 voltos.
D2=D20=1N4007 / legalább 1000 voltos.
Game port: R3=2.2M, R30=R31=10k.
C3=22n, Rezgőkör az oszcillátor f
rekvenciájára hangolva.T3=BC182
Kijelző egység: R4=22k, R40=10k, bi4=biztosíték, vagy 2-5 W
.T4=BC212 T40=BC182 D4=piros LED, H=20-50W -os hangszóró.
A DC/DC átalakító első fokozata egy ún. tranzisztoros blocking oszcillátor, amelyik megfelelő pozitív induktív visszacsatolással, (az L1 és L10 között), néhány tíz kHz-es frekvenciájú jelet állít elő. Ez a jel a kollektor köri rezgőkör megfelelő kihangolása miatt közelítőleg szinuszos alakú. Ezt – a veszteségektől eltekintve - a menetszámok arányá
ban (L2/L10) felszorozza a transzformátor.Ezt a közel szinuszos jelet a C20 és D2 alkatrészekből álló csúcs egyenirányítóra vezetjük. A kialakult egyenfeszültségre a C20 kondenzátoron keresztül ismét “ráül” (szuperponálódik) az L2-n megjelenő váltójel. Ezt egyenirányítja a D20 és C21 alkatrészekből összeállított egyenirányító, és így még hozzáadódik a már előtte kialakult egyenfeszültséghez. Ezzel a módszerrel sokszorozhatjuk a bemenő feszültséget, ugyanis, amennyi a fokozatok száma, kb. annyiszor lesz n
agyobb a kimenő feszültség.
A kialakult nagy (> 600 Volt) feszültséget – szabályozás szükségessége miatt – kettős potenciométerre vezetjük, ahová még egy szűrő kondenzátort (C22) tettünk. A potenciométer-páros segítségével a GM csőre jutó maximális, minimális feszültségek aránya kb. kétszeres, miközben a kapcsolási ötlet következtében, a legnagyobb kimenő feszültségnél terheljük le legkevésbé a sokszorozót.
Az illesztő fokozat a GM cső által előállított jel fázisát megfordítja, miközben elválasztja a nagyfeszültségű részt, - az esetleges károsodásokat elkerülendő - a PC érzékeny game portjától.
A kijelző egység, csak egy extra segítség, amely a méréshez nem feltétlen szükséges, de a hang és fény jelével iránymutatást ad a GM csövet érő sugárzás nagyságáról, változásáról.
Az “A, B, C, D, E, F, G” pontokat azzal a szándékkal vezettük ki a mérődoboz oldalára, hogy miközben azokon mérjük az áramkör jellegzetes adatait, lehetőleg minimálisan zavarjuk meg annak működését. Ezekre a pontokra kötött ellenállások é
rtékei ilyen szempont alapján lettek tervezve (R10=R30=R31=10kW , R2=R20=R22=10MW , R21=10GW ). Ismert az a (elkerülhetetlen) tény, hogy a mérés, mindig befolyásolja a mért rendszert, mégis sokszor nem vesszük figyelembe ezt, pedig ettől eltekinteni csak akkor jogos, ha a hatás (elhanyagolhatóan) kis mértékű.Az általunk, ebben a mérésben használt mérőműszerek (DVM, és a tízes osztóval ellátott oszcilloszkóp) bemenő ellenállása, gyári adatok szerint 10MW . Az elektronika alapjainak ismeretéből tudjuk, hogy - egyszerűbb esetben - a mérés befolyásoló hatása, a mért áramkör eredő belső ellenállása (Thevenin helyettesítő kép), és mérőműszer bemenő ellenállásának arányából kiszámolható (feszültségosztó képlet). Tudjuk, hogy az olyan áramkörök, amelyben félvezetök
(pl. diódák, tranzisztorok) vannak, azok nemlineáris tulajdonságuak. Ilyen a mi áramkörünk is. Ebből következik, hogy a mért belső ellenállás értéke függeni fog a mérés körülményeitől, de a kapott adatok pontosan jellemzik az áramkört. Később, amikor már izotóppal dolgozunk, a DVM-et fixen a ”D” pontra kell csatlakoztatni, így a GM-cső tápfeszültségét folyamatosan le tudjuk olvasni.A GM cső működése vázlatosan a következő:
Megfelelő gázzal, vagy gázokkal (pl. nemes gáz és alkohol molekulák keverékével) megtöltött hengeres, és elektromosan vezető cső közepébe egy vékony fémhuzalt helyezünk. A szálra, a külső hengerhez képest elegendő pozitív feszültséget adunk. A kialakult elektromos térerő, a radioaktív sugárzás hatására létrejött elektron-ion párok
at különböző irányba gyorsítva mozgatja, és az ütközések miatt újabb töltés-párokat létrehozva, az elektron kaszkádból kialakul egy szál mentén végigterjedő elektromos mikró kisülés. (3. ábra.)
3.ábra.
Ez az áram-impulzus a GM cső áramkörébe beépített m
unkaellenálláson, akár több voltos, feszültség-impulzusként megjelenve, már alkalmas közvetlen észlelésre, vagy további feldolgozásra. A mi áramkörünkben az R3-as ellenálláson keresztül bázisáramként vezérli a T3-as tranzisztort, és ezen keresztül a PC game portját.
A GM cső feszültségét növelve a 4. ábrán. látható jellegzetes karakterisztikát kapjuk. Részletes elméleti magyarázatot mellőzve (hiszen ez nem feladata ennek a laboratóriumnak) azt tudjuk mondani, hogy az első ún. ionizációs (i) szakasznál még nem elegen
dő az elektromos térerő az ütközéses sokszorozáshoz, így csak a radioaktív sugárzás által közvetlenül létrejött elektron-ion párok elmozdulva az anódra (középső szál), és katódra (külső henger) ionizációs áramot hoznak létre. A feszültséget tovább növelve (második: p = proporcionális szakasz) mind több, és több ütközés történik, ami már sokszorozási jelenség. Ezek után következik egy majdnem vízszintes (más néven G = Geiger) szakasz, amikor már a sokszorozási jelenség telítésbe kerül, és ezért a keletkezett impulzus amplitúdója majdnem független a csőre adott feszültségtől.A lavina effektus gyors kialakulását (fotonok segítségével) elősegíti a hengeres katód belső felületének jó fotó-elektromos hatásfoka.
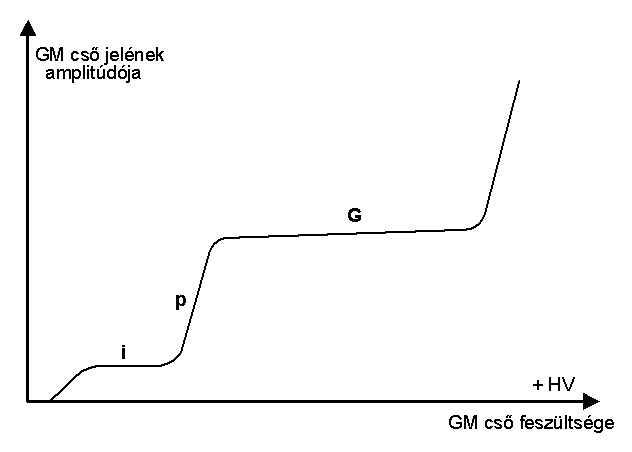
4.ábra.
Felmerül az a kérdés, hogy mitől szűnik
meg a kisülés?Anélkül, hogy nagyon elmélyednénk a részletekben, két alapvető jelenséget kell megemlíteni.
Az egyik az, hogy a kaszkád következtében az anód-szál körül kialakuló töltés-felhő sokszorozási küszöb alá csökkenti az elektromos térerőt, s így ez a sokszorozás leállásához vezet. Ugyanez lesz az eredmény, ha a GM csővel sorba elegendően nagy munkaellenállást rakunk, mivel így az átfolyó impulzus-áram a csövön akkora feszültségcsökkenést okoz, hogy a sokszorozás szintén leáll. Elektronikus módsz
errel is leállítható a kisülés, ha a kialakuló impulzust, vezérlésként is felhasználva, rövid időre lekapcsoljuk a GM cső tápfeszültségét.A másik jelenség, ami szintén a kaszkád kialakulása ellen hat, (illetve megszüntetni igyekszik azt), az a rekombináció jelensége. Ez azt jelenti, hogy a már kialakult elektron-ion párok ismét egyesülve csökkentik a kaszkád lehetőségét. Minimális alkohol molekula hozzáadása a GM cső gáztöltéséhez szintén elősegíti a kisülés gyors leállítását.
Mérési adatok pontossága.
Először felsoroljuk a hibák három típusát:
a./ Tévesztéses (baklövés vagy durva) hiba. Ilyenek pl. téves leolvasás, adat elírás, elvi félreértés, mértékegység és nagyságrend keverés, más szóval durva figyelmetlenség. Ezekre nyilvánvalóan az jellemző, hogy nem találhatunk bennük semmi “törvényszerűséget“.
b./ Szisztematikus hiba. Oka, pl. a rossz (vagy már idővel megváltozott) műszerkalibrálás, illetve környezeti paraméterek (pl. hőmérséklet, légnyomás, tápfeszültség stb.) változásának hatása. Jellemző rájuk, hogy a mérések ismétlésekor ugyanaz a hiba, ugyanolyan módon rontja el az eredményt.
c./ Statisztikus (véletlen) hiba. Az jellemzi, hogy az azonos körülmények, és feltételek mellett kapott mérési eredmények a jó (» várható, átlagos, közép, illetve valódi?) eredményhez képest mindkét irányba, nagyjából egyforma súllyal térnek el. Ennek oka főleg az, hogy nem ismerjük (esetleg jelenleg nem is ismerhetjük) a mért jelenség mélyebb törvényeit, vagy nem tudjuk (akarjuk) figyelembe venni őket, illetve nem tudjuk pontosan leolvasni a mérőeszközökről az adatokat.
Jellemző, hogy, ha a mérést többször (sokszor) megismételjük, akkor a fent említett okok miatt, az eredményeink nem lesznek teljesen egyformák, más szóval a mérési adataink szórni fognak. Amíg az analóg méréstechnikában, nem csak a módszerből eredhet a pontatlanság, hanem a szemünkkel leolvasott értékek is szórnak, addig a digitális technikában a számjegyek leolvasásánál nem lehet véletlen hibát elkövetni, viszont a statisztikus hibák bármely folyamatban, pl. észlelésnél (jeladók), erősítésnél, jelátalakításnál (AD, DA) szintén előfordulnak.
Mi ebben a mérésben, csak ezzel a harmadik típussal foglalkozunk, mivel a radioaktív atommagok véletlenszerűen és egymástól függetlenül bomlanak.
Általánosságban vizsgáljunk meg egy (“N” darabos) mérési eredmény sorozatot, amelynél az egyes adatok (xi) egy közepes érték (![]() ) körül véletlenszerűen szórnak. Logikus, hogy minél több adatot gyűjtünk be és átlagolunk annál pontosabban, közelíthetjük meg a várható értéket:
) körül véletlenszerűen szórnak. Logikus, hogy minél több adatot gyűjtünk be és átlagolunk annál pontosabban, közelíthetjük meg a várható értéket:
![]()
![]()
A hibaszámítás összefüggéseit felhasználva az egyes mért adatok hibája (egyszeres szórása:s ) az alábbi:
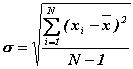 ,
,
illetve az ![]() (várható érték) szórása:
(várható érték) szórása: ![]()
Valószínűségszámítás és kombinatorika megfelelő törvényeit alkalmazva a véletlenszerű (statisztikus) jelenségre, valamint felhasználva néhány ügyes gondolatmenetet, és matematikai összefüggést, az alábbi összefüggéshez jutunk:
![]()
A képlet azt mondja meg, hogy mekkora (P) valószínűsége van annak, hogy éppen egy “k” értéket mérjünk, miközben az “![]() “ a várható érték. Természetesen “P” a 0 (0% valószínűség) és az 1 (100% valószínűség) közötti értékeket veheti fel.
“ a várható érték. Természetesen “P” a 0 (0% valószínűség) és az 1 (100% valószínűség) közötti értékeket veheti fel.
Ezt az összefüggést nevezik Poisson eloszlásnak. (5.ábra.)
Tovább folytatva, - az itt nem részletezett számítást - megkapjuk, hogy itt a s
(szórás) egyenlő a mért érték gyökével, és így az alábbi módon írhatjuk le egyszerre a mért értéket, és annak a hibáját (egyszeres szórását):![]() . A relatív hiba:
. A relatív hiba: 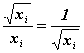 , százalékban:
, százalékban: ![]() %.
%.
[Amikor egy mérési sorozat átlagértéke ![]() , akkor a mért értékek (xi–k), kb.68%-a az
, akkor a mért értékek (xi–k), kb.68%-a az ![]() (egyszeres szórás), a 95%-a a
(egyszeres szórás), a 95%-a a ![]() (kétszeres szórás), és majdnem minden adat (99,8%) a
(kétszeres szórás), és majdnem minden adat (99,8%) a ![]() (háromszoros szórás) tartományokon belül kell, hogy legyen.]
(háromszoros szórás) tartományokon belül kell, hogy legyen.]
Amennyiben a mérések (események) száma jelentősen növekszik, akkor már a Poisson összefüggést mind jobban közelíti az ún. Gauss eloszlás:
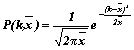 ,
,
Ugyanúgy, mint a Poisson eloszlásnál ez a képlet is azt mondja meg, hogy mekkora (P=0,..,1,ill. PÎ
[
0,1]
) valószínűsége van annak, hogy “k” értéket mérjünk, miközben az “![]() “ a várható érték.
“ a várható érték.
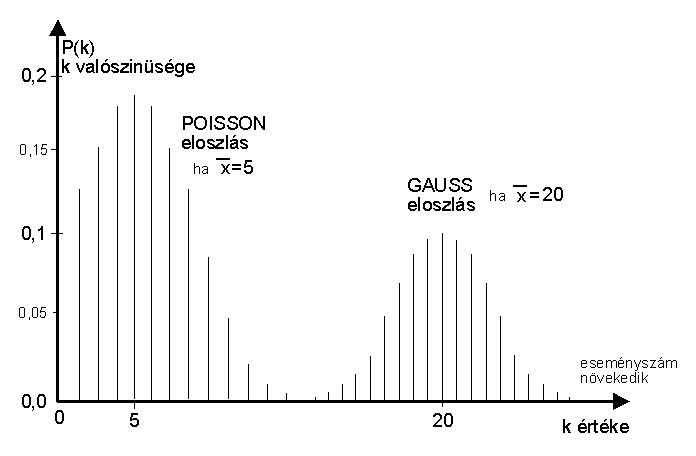
5.ábra.
Az 5. ábrán a szemléletes összehasonlíthatóság kedvéért együtt ábrázoltuk ugyanannak (de nyilvánvalóan különböző módon elvégzett
) mérésnek, a Poisson, illetve Gauss eloszlását. Látszik, hogy amikor jóval nagyobb az eseményszám (az ábrán 4-szer), akkor már a Poisson eloszlást jól közelíti a Gauss eloszlás.Az elméleti összefoglaló után, vizsgáljuk meg, hogy milyen jellegzetessége van az általunk mért statisztikus radioaktív sugárzásnak. Az időben véletlenszerűen keletkező, (de a GM cső által csak néhány százalékában detektált) impulzusokat megfelelő ideig begyűjtjük. Minden beérkező impulzusnak lejegyezzük az időpontját, így a memóriában kapunk egy eseménynaptárt (t1, t2, ….tn), amit mi idősornak neveztünk el. Ebből az adathalmazból két különböző (idő, illetve beütésszám) eloszlást tudunk előállítani. Ezen két eloszlás nyilvánvalóan egymásnak mintegy a “reciprokai“, hiszen ha az események sűrűsödnek, akkor az időtávolságok csökkennek, viszont a beütésszám (azonos idő alatti eseményszám) meg növekszik.
Az idő és beütésszám eloszlásának előállítási módja, ábrázolása a következő részben, a mérő-kiértékelő: “sugjel.exe“ program leírásában megtalálható.
Megértve a programot, észre kell vennünk, hogy az időeloszláson nem kell, (igaz szoftveresen nem is tudunk módosítani) hiszen az időkülönbségeket csak a komplett mérőrendszer fizikai adatai határozzák meg. Ilyenek, pl. az izotóp aktivitása, és távolsága a GM csőtől, a detektor hatásfoka, vagy tápfeszültsége, esetleg a rendszer holtideje stb.
Ez azt jelenti, hogy a “felbontást” változtatva csak az ábrázolás minőségét és nem az adatsorok tartalmát
befolyásoljuk Pl. amikor csak a mérő-kiértékelő programmal tekintjük meg előzetesen az beütésszám eloszlást, akkor (mivel a beütésszám csak egészszám lehet), a jó ábrázolás érdekében, célszerű, hogy a maximális és minimális beütésszám különbsége a “felbontás” egészszámú többszöröse legyen
Egyazon idősorból előállított beütésszám eloszlásra (attól függően, hogy mekkora mérési és kapuidőt választottunk), különböző eloszlásokat illeszthetünk:
Kis kapuidőt választva , kevés lesz az esemény (pl. csak néhány beütés/kapuidő), ekkor a görbét a Poisson eloszlás közelíti meg pontosabban.
Most állítsunk be jóval nagyobb kapuidőt. Ekkor sokkal több lesz az esemény (pl. legalább néhány tíz beütés/kapuidő), és már megengedett, hogy Gauss eloszlást illesszünk a mért adatokra.
.
A “Sugjel.exe“ mérő-kiértékelő program ismertetése:
A program a számítógép game-portjára csatlakoztatott GM csöves beütésszám-mérő szoftver oldali része. A program mérő, feldolgozó és megjelenítő funkciókat lát el.
Feldolgozás / Monitor Ezzel a menüponttal ki ill. bekapcsolhatjuk az a
ktuális beütésszám-megjelenítést. Ez a funkció inkább diagnosztikai és ellenőrzési célokat szolgál, mérési feladatokra inkább a következő menüpontot használjuk.Feldolgozás / Adatgyűjtés (idősor)
menüpont hatására egy újabb ablak nyílik, ahol beállíthatjuk a mérés időtartamát (óra:perc:másodperc). Start gomb megnyomásával indul a mérés, ami lényegében az egyes beütések időpillanatainak feljegyzését jelenti. Ennek eredménye az alábbi sémán látható t1, t2, ... tn idősor. A mérés addig tart, amíg:-le nem tel
ik az előre beállított időtartam,-"S" gombbal le nem állítjuk,
-a beütésszámok száma el nem éri (az ini.-ben beállított) pl. az 500 ezres értéket.
Az így nyert idősor File / Idősort fileba ment menüponttal szöveg fileba menthető. Ez a művelet időigényes lehet akkor, ha az idősor túl hosszú és lassú géppel dolgozunk. File / Idősort fileból betölt művelet éppen az előző ellenkezője. Segítségével korábban lementett idősor tölthető vissza ismételt feldolgozás céljából.
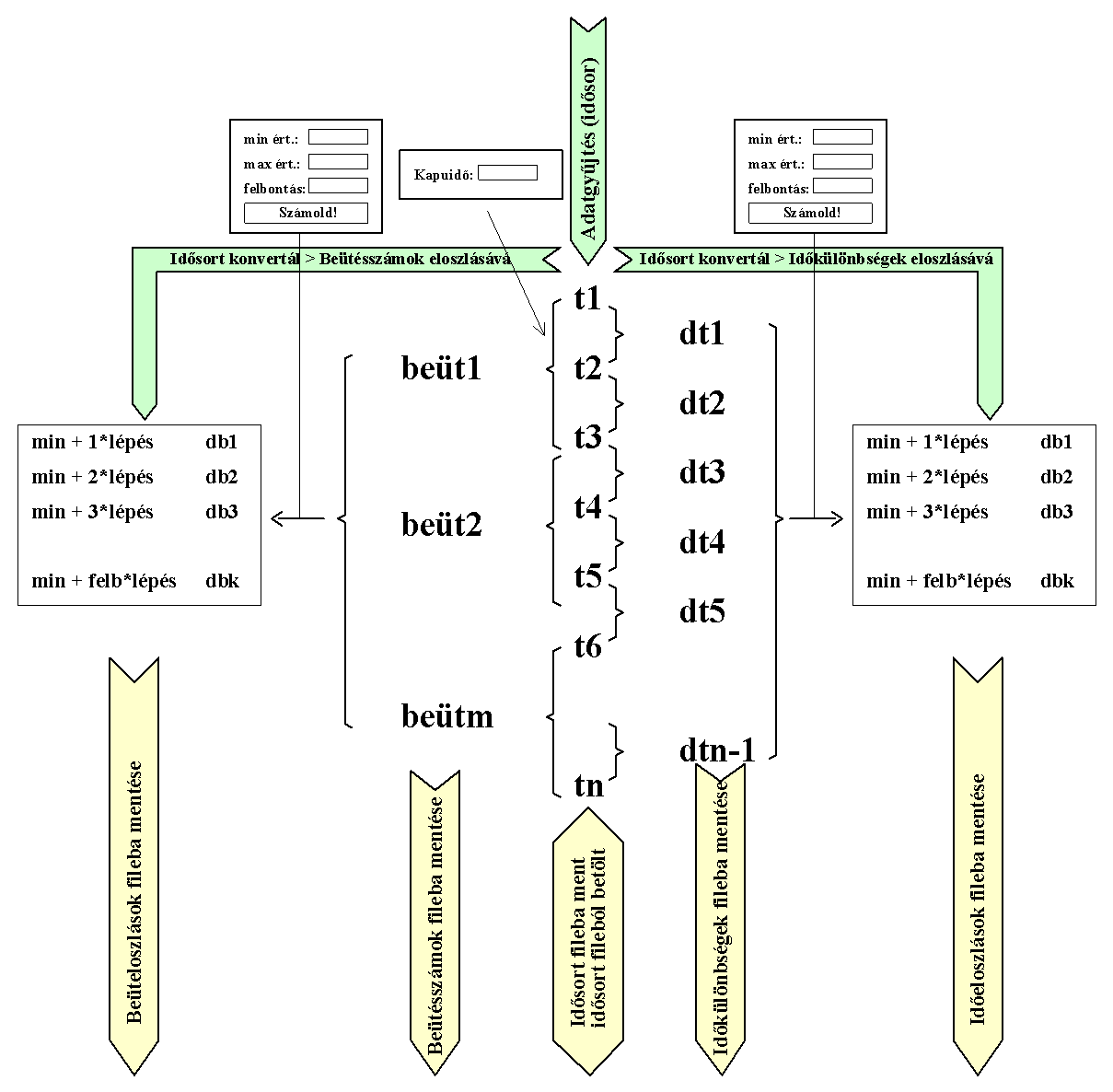
Feldolgozás / Idősort konvertál –> Időkülönbségek eloszlásává.
A program t1, t2, ... tn időpillanatok különbségét képezi: dt1=t2-t1, dt2=t3-t2, ... Ezután meghatározza a dt-k minimum és maximumát. Ezt látjuk egy újabb dialógusablakban. Ha a dt-k egy szűkebb tartományára szeretnénk elkészíttetni az eloszlást, akkor az itt közölt minimális és maximális érték felülbírálható, megváltoztatható. Ugyancsak itt kell megadnunk, hogy mekkora felbontással vizsgálódunk, hány "elemi csatornára" bontjuk a [min, max] intervallumot. Számold! gomb hatására elindul az eloszlás számítás. Az eredmény rövid időn belül grafikusan is megjelenik. A grafikon területén "zoomolhatunk", ha a bal egér gomb nyomva tartása mellett (balról-jobbra és fentről-lefelé) kijelölünk egy tartományt, ill. ennek ellenkezőjét válthatjuk ki ellentétes mozgású tartomány kijelöléssel. Mind a dt-k tömbje, mind pedig az eloszlás eredménye fileba menthető az Időkülönbségek fileba mentése ill. Időeloszlások fileba mentése gombokkal! (Az előbbi lényegesen nagyobb file szokott lenni, mint az utóbbi!)Feldolgozás / Idősort konvertál –> Beütésszámok eloszlásává.
Először a beütések pillanatainak t1, t2, ... tn tömbjéből beütésszámokat készít a program úgy, hogy miközben végig megy a fenti tömbön, megnézi, hogy a felhasználó által megadott kapuidőn belül hány beütést talál (lásd a program működésének sémáját). A program meghatározza a beütésszámok minimum és maximum értékeit. Ugyancsak a felhasználó dolga megadni, hogy mekkora felbontással készüljön az eloszlás. Számold! gomb megnyomására indul az eloszlás számítás, befejezéséről a grafikon felbukkanása tájékoztat. Mind a beütésszámok tömbje, mind pedig az eloszlás eredménye fileba menthető a Beütésszámok fileba mentése ill. Beütéseloszlások fileba mentése gombokkal!Mérés tervezése:
Először azt kel
l eldöntenünk, hogy hány pontból próbáljuk majd felrajzolni a Poisson, vagy Gauss görbénket, majd az egyes pontokhoz mennyi eseményt, beütésszámot (xi–ket) gyűjtsünk össze, hogy megfelelő legyen a pontosság. Emlékezzünk a pontosság:Ez azt jelenti, hogy 1%-hoz több mint tízezer, vagy a 10% pontossághoz több mint 100 eseményt kell begyűjtenünk, illetve ezeknek célszerű a 2-3-szorosát begyűjteni, a már előzőekben elmagyarázott többszörös szórás (hiba) jellegzetessége miatt. Emlékezz
ünk vissza az 1-2-3-szoros szórás lényegére.Egy példa: 100 pontot, kb. 5%-os hibával szeretnénk felrajzolni. Ez pontonként kb. 2-3 ezer beütést, vagyis összesen kb. 2-3 százezer eseményt jelent. Ekkor, ha monitor állásban a másodpercenkénti beütésszámot leolvassuk (a példa kedvéért ez most legyen 70) ki tudjuk számolni a szükséges mérési időt. Ebben a példában így nekünk 3-4 ezer másodpercig (kb. egy óráig!) kell mérnünk.
A megfelelő adatmennyiség begyűjtését befejezve és elmentve, - nem feledve, hogy ha pl.100 pontot szeretnénk ábrázolni, - a kapuidőt úgy kapjuk meg, hogy a teljes mérési időt elosztjuk 100-al, vagy ennek egészszámú többszörösével. (Vigyázat ezt ne keverjük össze a mérő program ábrázolási részénél szükséges felbontással, de mint említettük már, ott is célszerű a tartományok egészszámú felosztása!)
Kivonatos ismeretek a “GNUPLOT” rajzoló, illesztő programról.
Általánosságban érdemes néhány gondolatot megemlíteni erről a programról is, aminek segítségével a mért göbéket megrajzoljuk,
illetve amellyel a mérési adatokra illesztjük az elméleti görbét. Mivel a méréshez mellékelve van (és a hálózaton is megtalálható) egy részletesebb leírás, ezért itt csak az ide speciálisan, és feltétlenül szükséges parancsokat soroljuk fel.Sokszor, nekünk kell elkészítenünk a gnuplot részére emészthető adat formátumot. (Természetesen, amikor a formátum eleve jó, akkor ezt nem kell megtenni, ilyen, pl. a “sugjel.exe” program által előállított beütésszám eloszlás adatsor: “eloszlas.rte”.)
Szükséges formátum lehet, pl. egy notepaddal írt textfájl (mondjuk: “adat.txt”). A lényeges az, hogy (pl. X, Y, Z, stb.) adatsorok tabulátorral, vagy szóközzel elválasztott külön oszlopokban legyenek. Egyszerűség kedvéért célszerű, ha ez a fájl a gnuplot könyvtárába kerül.
Amennyiben az Y-t (és annak hibáját is) az X függvényében ábrázolni akarjuk, akkor azt írjuk, hogy:
plot “név1.txt” using 1:2:(sqrt($2)) with xerrorbars
Amennyiben, csak simán vonalas ábrával akarjuk az Y-t az X függvényében ábrázolni, akkor azt is elég írnunk, hogy:
plot “név1.txt” using 1:2 with linepoints
Illesztéshez, pl. írható ez is:
fit f(x) “név1.txt” using 1:2:(sqrt($2)) via a,b,c
Ahol “f(x)” egy előzőleg beírt, konkrét elméleti görbe képlete, és az “a,b,c” pl. az ebben szereplő paraméterek, amit nekünk kell lehetőleg jól saccolva, kezdő paraméterként megadni.
Paraméterek száma természetesen az illesztendő függvény bonyolultságától függ.
A kinyomtatáshoz először a plot (Gnuplot graph) ablakában nyomjunk egy jobb gombot, és a legördülő menü-ablakban rákattintunk a “Print”-re. Ezután megjelenő “nyomtató beállítás”-ban nyomjunk egy “OK”-t, és így már be tudjuk állítani a grafikonunk tetszés szerinti méretét és helyzetét. Segítségül példaként a mérőhelyen található egy (célszerű) nyomtatási adatlap.
Általánosságban elmondottak mellett, célszerűnek tartjuk a statisztikai mérésekhez még egy kis
speciális segítséget nyújtani, különös tekintettel arra, hogy miként írjuk le az elméleti görbéket “gnuplotos” formában.1./ Poisson formula: 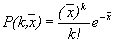
célszerűbb jelölésekkel: 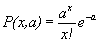
A gnuplotban a faktoriális (x!) helyett a hasonló, de több lehetőséget felkí
náló gamma(x) függvény használjuk fel. [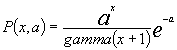 ,
,
és paraméteres gnuplot formátumban:
f(x) = b*((a**x)*exp(-a))/gamma(x+1),
a képletben szereplő “a”az átlag, “b”: az átlag helyén a m
aximum.
2./ Gauss formula: 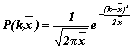 , fenti jelölésekkel:
, fenti jelölésekkel: 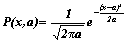
ez a képlet paraméteres gnuplot formátumban:
f(x) = b*(1/sqrt(2*pi*a))*exp(-((x-a)**2/(2*a)))
Itt is az “a”: az átlag, és “b”: az átlag helyén a maximum.
3./
Most egy példán keresztül bemutatunk egy lehetséges rajzolási, illesztési menetet.
Természetesen más fájlnevekkel és módon is el lehet végezni a feladatot.
(Részletesebb segítséget a gnuplot leírásban, illetve helpben találhatunk.)
Kezdeti paraméterek becslése:
Logikus, hogy a “sugjel.exe”-ből kapott, és a legjobbnak látszó beütésszám eloszlásból (ennek neve, pl. “
eloszlas.rte”) tudjuk leolvasni az “a”-t, illetve “b”-t.A példa kedvéért legyen, a=370, és b=25, így a “gnuplot”-ba a következőket célszerű beírni:
a=
370b=
25Érdemes beállítani az ábrázolási tartományt, ami pl. a várható érték ±
legalább a háromszoros szórás (a±
³
3![]() ) lehet. Példánkban ez: 370 ±
60 (vagy akár: 370 ±
100), így:
) lehet. Példánkban ez: 370 ±
60 (vagy akár: 370 ±
100), így:
set xrange [
Majd definiáljuk a szükséges elméleti függvényt:
f(x)=… pl.
az előzőekben leírt függvények valamelyike.Most már (tetszés szerinti formátumban) megnézhetjük a függvényünket:
plot f(x)…….
+a szükséges paraméterekIllesztésnél, pl. az alábbi formulát írhatjuk le:
fit f(x) “
eloszlas.rte” using 1:2 via a,b(Ne felejtsük el az illesztett paraméterek adatait, hibáival együtt a jegyzőkönyve beírni!)
Végül, pl. egy grafikonon ábrázolhatjuk a mért és illesztett elméleti görbénket:
plot f(x), “
eloszlas.rte” using 1:2 with errorbarFigyelem: a döntött, és halványabban írtak helyére a saját adatot, és fájlnevet kell beírni!!