Alaptörvények
A./ Ohm törvény
A vezetési jelenségek
megfigyelésébõl arra következtethetünk,
hogy a vezetõ belsejében a töltést mozgató
térerõsség vektor (E)*,
és az áramsûrüség vektor (J)*
között arányosság van. Arányossági
tényezõ a g
fajlagos vezetés. Ennek az összefüggésnek
általános (vagy szokásosan differenciális)
Ohm törvény a neve :
J = g E. Al. 1
A g fajlagos vezetés az anyagra jellemzõ adat, és az értéke nagyságrendileg (fémes vezetõkre) 107 A/Vm.
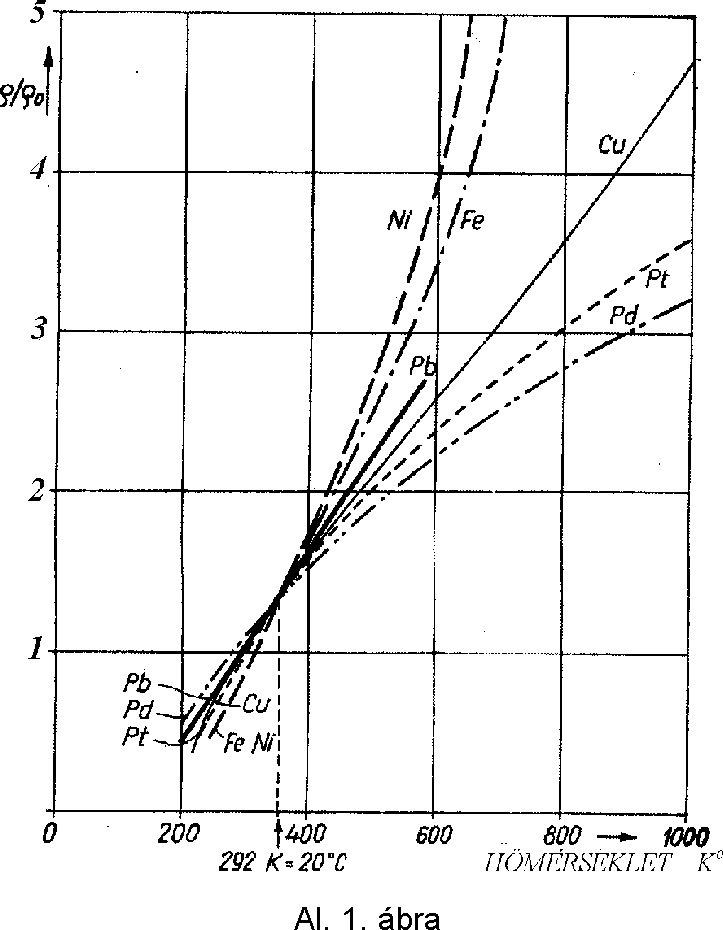
Az anyagnak általában van karakterisztikus hõfokfüggése, ami az Al. 1. ábrán jól látható, de amit sokszor elhanyagolunk.
A gyakorlatban elterjedtebb mennyiség a fajlagos ellenállás a r :

r = 1/g . Al. 2
Igy az Al. 1 átírható:
E = r J. Al. 3
Az ellenállás (rezisztencia R) és a fajlagos ellenállás a r között - ha feltételezzük az anyag homogenitását - az alábbi logikusan következõ (definíciószerû ) összefüggés van:
R = r l/a. Al. 4
A képletben "l" (m) az illetõ anyag hossza és "a" a keresztmetszete (m2) . Figyelembe véve az Al.3 és az Al.4 összefüggéseket, valamint beírva a dimenziókat, definiálhatjuk az ohm egységét :
1 W (ohm) = 1 V/A. Al. 5
* ( A vektor egy olyan mennyiség, amelynek nemcsak nagysága, hanem iránya is van.)
Az ellenállás reciproka a vezetés, amelynek egysége a siemens (S):
1 S (siemens) = 1 A/V. Al. 6
(Ezt néha " mho "-nak is jelölik.)
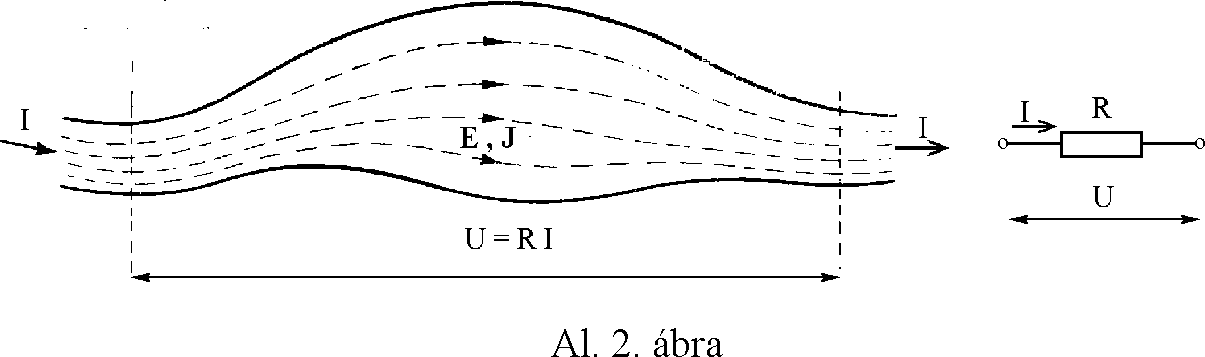
Nézzük az Al. 2. ábrát, amelyen látható elektromos vezetõben I nagyságú áram folyik és ennek hatására a két szaggatott jel közötti ellenállás részen U nagyságú feszültség jelenik meg. Az arányossági faktor az R ellenállás (Al. 7). Ez kísérletileg bizonyított, de az áramlási tér törvényeinek linearitását kihasználva, - ami az elméleti szakirodalom megfelelõ fejezeteinél bizonyítva van - az Al.3-ból is megkaphatjuk a jól ismert Ohm törvényt :
U = RI ( I = U/R, R =U/I ) Al. 7
A feszültség Volt, az áram Amper és az ellenállás Ohm dimenziójú.
A középiskolában már megismertük, és most csak felelevenítjük a fém anyagú ellenállások hõfüggésének közelítõ képletét*:
R(q ) = R(q 0)[1+a 0(q - q 0)], Al. 8
ahol q a hõmérséklet (q 0 = 200 C), és a 0 (dimenziója 1/ 0C) a hõfoktényezõ. Ennek a tényezõnek fémes vezetõkre » 4× 10-3/ 0C a közelítõ értéke. ( 25 0C hõfokváltozás kb. 10% ellenállás különbséget eredményez! ) Ez a képlet nem veszi figyelembe a hõtágulást, és a lineáris közelítés csak szobahõmérséklet közelében és legfeljebb 100 0C tartományban használható. Vannak azonban olyan speciális ötvözetek, amelyek ellenállásának hõmérsékletfüggése jóval kisebb az általában ismert értéknél. Ilyenek pl. a manganin, krómnikkel, konstantán stb.
* Sokaknak ismertebb lehet a fajlagos ellenállás hõmérsékletfüggése.
Meg kell említenünk a szupravezetés jelenségét is, amely azt jelenti, hogy egy jellemzõ (általában nagyon alacsony) hõmérsékleten bizonyos, -de nemcsak fémes - anyagok teljesen elveszítik az ellenállásukat.
Azt biztosan mondhatjuk, hogy jó minõségû ellenállások (bár ez igaz más elektronikus alkatrészekre is) elõállításához, gyártásához nagy körültekintés szükséges. Az ilyen alkatrészeket lehetõleg pontosra, hõfüggetlenre, idõben stabilra és alacsony parazita (C, és L) komponensûre kell készíteni. Ezeket a feltételeket - a köznapi elektronikus áramkörökben - az ún. fémréteg ellenállás egészen jól kielégíti.
Az ellenállások linearitása
Amikor egy vezetõn különbözõ nagyságú áram folyik, és ennek hatására annak ellenállása nem változik, akkor mondhatjuk, hogy a vezetõ - mint ellenállás - lineáris. Ezt az összefüggést ábrázolja az "R" jelölésû egyenes ( Al. 2/a. ábra ).
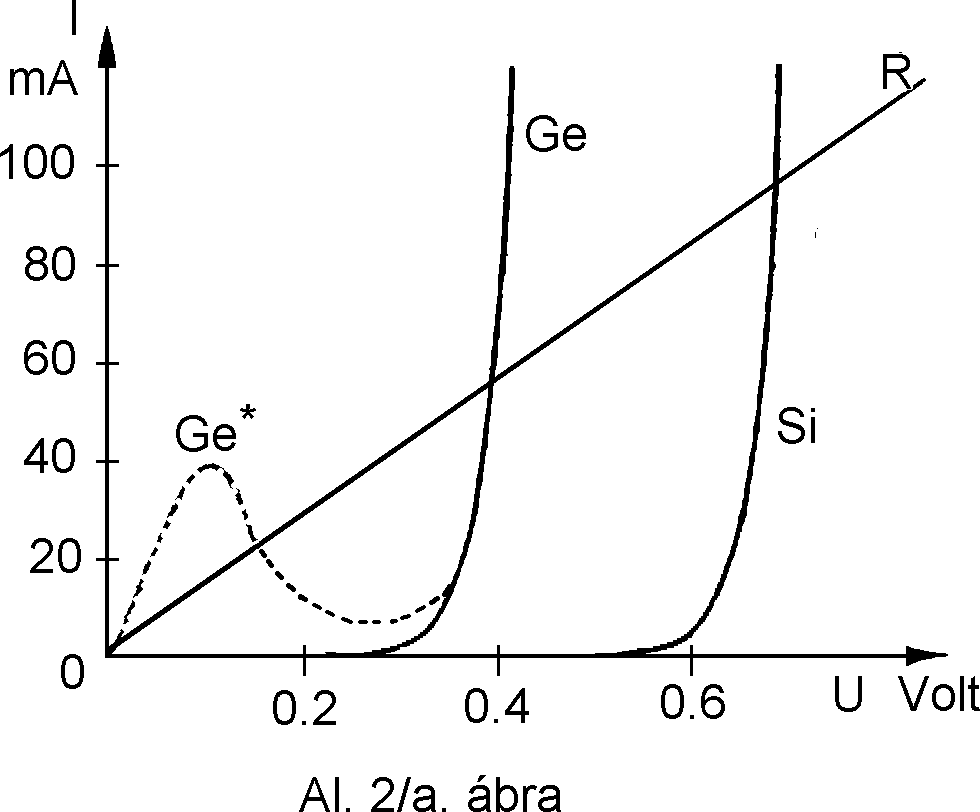
Az ábrán még egy germánium dióda (Ge), egy szilícium dióda (Si) és egy germánium alagút dióda (Ge*) karakterisztikáját is ábrázoltuk. Az alagút (tunel vagy Esaki) dióda szaggatott vonallal kezdõdik és a "Ge" jelölésû görbében folytatódik. Láthatjuk, hogy ezek a görbék nem lineárisak az U-I koordináta rendszerben, azaz minden egyes pontban más az ellenállás értéke. Két lehetõségünk is van a számolásra.
Az egyik: elosztjuk az alkatrészen esõ feszültséget a rajta átfolyó árammal, igy kapott értéket egyenáramú (sztatikus) ellenállásnak nevezzük.
A másik: a görbe aktuális pontjába érintõt illesztünk - ez az ún. differenciális (vagy dinamikus) ellenállás.Vegyük észre, hogy általában a kettõ nem azonos, sõt akár sok nagyságrenddel is különbözhetnek egymástól.
Van egy még érdekesebb jelenség is, az ún. "negatív" ellenállás, ami az ábrán elég jól látható. Természetesen nem a sztatikus érték negatív, hiszen ez értelmetlen lenne (miért?), hanem a differenciális ellenállás (az érintõ meredeksége) lesz negatív. Az alagút dióda karakterisztikájában van egy ilyen tartomány is, - két inflexiós pont között - ahol ez jelenség fellép. Ez a szakasz instabil állapotot jelenthet, s emiatt általában az eszköz itt tartósan nem maradhat. Késõbbi fejezetekben (pl. a félvezetõknél) még más "negatív" ellenállású eszközzel (diak, tirisztor, triak stb.) is megismerkedhetünk.
B./ Soros, párhuzamos kapcsolások és osztók
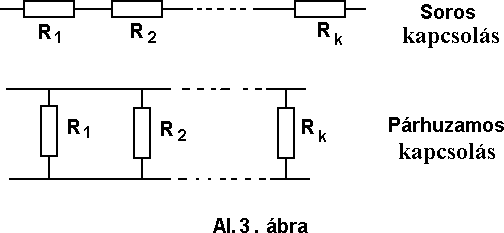
1./ Ellenállások (impedanciák) sorba kapcsolásakor az eredõ érték az egyes elemek összege lesz: (Megértéshez az Al. 4 képlet és az Al. 2. ábra is segítséget ad.)
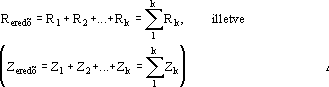
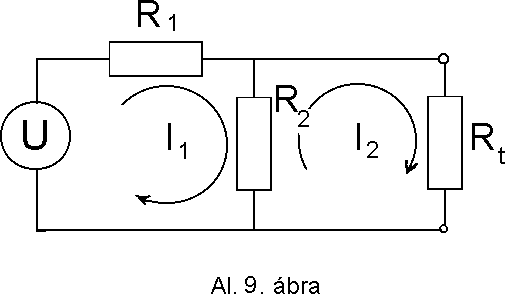
Al. 9.
2./ Az elõzõ pontban követett gondolatmenetet továbbfejlesztve a párhuzamosan kapcsolt ellenállások (impedanciák) eredõje az alábbi lesz:
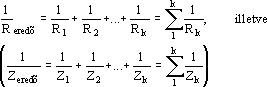
Al. 10
Az Al. 9. és Al. 10. képletekben a Z impedanciák komplex és nem abszolút értékek!
3./ Feszültségforrásokat illetve feszültséggenerátorokat sorbakötve a feszültségeik (elõjelhelyesen) és a belsõ ellenállásaik (egyszerûen) összeadódnak. Késõbbiekben látni fogjuk, hogy ezen elemek párhuzamos kapcsolása már bonyolultabb számítást, és több figyelmet igényel!
Az áramforrásokat és áramgenerátorokat párhuzamosan kötve az áramok elõjelhelyesen összeadódnak, és a belsõ ellenállásaik eredõjét az elõzõ pontban (2./) leírt párhuzamos kötés törvénye alapján kapjuk meg. Amikor ilyen elemeket sorba kötünk, akkor az eredõ kiszámolása már sokkal nagyobb nehézséggel jár.
(A 3.-as pontban leírtak a Kirchhoff törvények megismerése után és annak alkalmazásával még könnyebben megérhetõk lesznek.)
4./ A feszültségosztó megértéséhez elég az Ohm törvény ismerete:
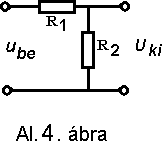
Mivel terhelés nélkül az R1 és R2 ellenállásokon átfolyó áram I = Ube/(R1+R2),
[Z1 és Z2 impedancia mellett I = Ube/(Z1+Z2)]
és Uki = IR2 , így:
![]()
C./ Thevenin és Norton törvények
A Thevenin tétel azt fogalmazza meg, hogy azok az elektromos hálózatok, amelyek lineáris áramköri elemekbõl, valamint feszültség és áramforrásokból (generátorokból) állnak, azok mindig helyettesíhetõk olyan kétpólussal, amely egy feszültségforrásnak és egy impedanciának* soros eredõjébõl áll (Al. 5.a ábra).
A Norton tétel szinte teljesen azonos az elõzõ törvénnyel, csak a helyettesítõ kétpólus egy áramforrás és egy vele párhuzamosan kapcsolt impedancia*(Al. 5.b ábra). Terhelés nélkül az áramkör kimeneti pontjain itt is az eredõ ún. üresjárási feszültséget kapjuk.
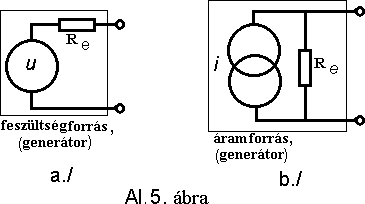
E két tétel az egyszerûsítõ ötleten kívûl, segítséget nyújthat az elsõ ránézésre bonyolultnak, és nehezen kiszámolhatónak tûnõ áramkörök problémáinak megoldásánál is.
*Természetesen amikor az áramkörben csak ellenállások vannak (a forrásokon és generátorokon kívül), akkor az impedanciák helyett ellenállások szerepelnek.
D./ Kirchhoff törvények
Csomóponttörvény (elsõ törvény)
Ez a törvény a töltésmegmaradás elvét alkalmazza. A csomópontban (áram-elágazási pont) találkozó áramok algebrai összege nulla, mert ha ez nem így lenne, akkor itt töltések (Q) halmozódnának fel (Al. 6. ábra). Mivel az áram az idõegység alatt áramló töltés (I = Q/t), így a törvény az alábbi, közismert alakban is felírható :

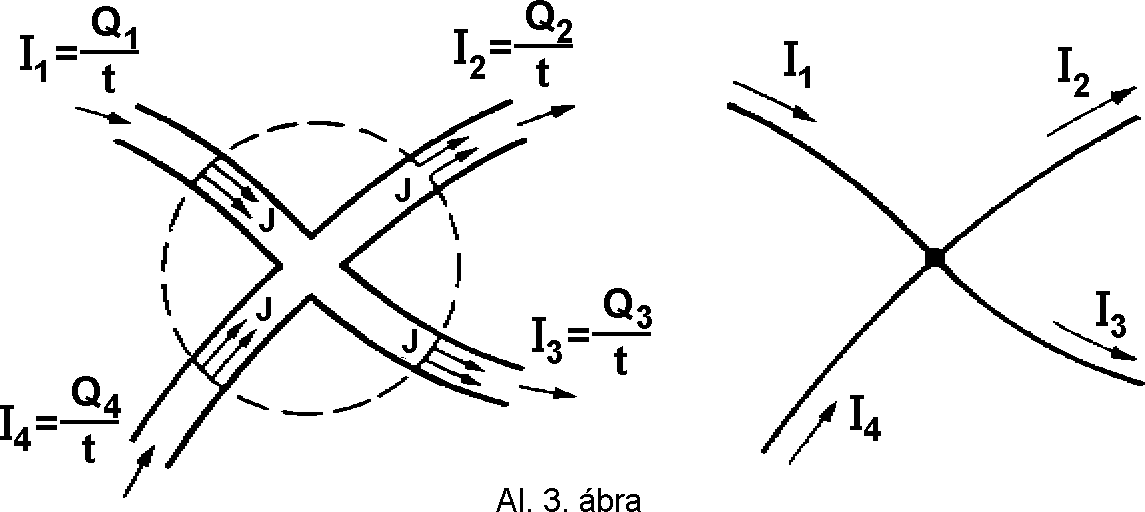 Al. 6.
ábra
Al. 6.
ábra
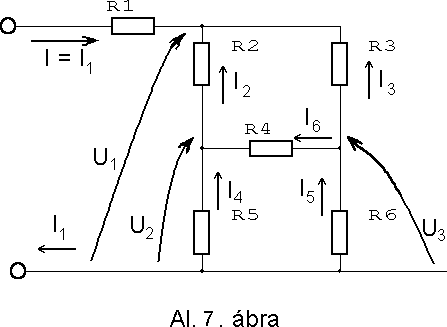
Gyakorlatban a törvényt felhasználva úgy kell számolunk, hogy az Ohm összefüggés segítségével meghatározzuk minden egyes csomópontba be és kifolyó áramot, és ezeket elõjel-helyesen összeadjuk.
A számoláskor úgy is eljárhatunk, hogy minden csomóponthoz rendelünk egy "Uk" feszültséget -tetszõleges iránnyal - valamilyen másik csomóponthoz képest, és feszültségkülönbségekbõl így már ki tudjuk számolni az alkatrészeken átfolyó áramokat :
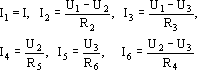
Ezután használjuk fel a Kirchhoff elsõ törvényét (Al. 12.), de itt már vigyáznunk kell az áramirányok helyességére is:
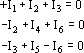
A négy csomópontra természetesen négy
egyenletet írhatnánk fel, de a negyedik összefüggés
( -I1-I4-I5= 0 ) már nem adna (nem is adhat, hiszen csak három
ismeretlenünk van: U1, U2 és U3 ) újabb független
összefüggést. Az áramok fent kifejezett értékeit
helyettesítsük be, így az U1, U2 és U3 már
kiszámítható. Ezek ismeretében az áramkörben
folyó áramok is meghatározhatók lesznek.
(Felvehettünk volna még egy feszültséget pl. az U4 -et (R4 -en mérhetõ érték), de ez sem jelentene újabb független adatot ( U4= U2-U3 ), hiszen az R4 -en átfolyó áramot (I6) már meghatároztuk, vagyis csak annyi független egyenletet hozzunk létre, ahány ismeretlen adatunk van.)
Huroktörvény (második törvény)
Ez a törvény azt mondja ki, hogy bármely zárt hurokban, ha elõjelhelyesen összeadjuk a feszültségesések (IR) algebrai összegét és a feszültségforrások belsõ feszültségei algebrai összegét, akkor nullát kapunk eredményül.
![]()
Az Al. 8. ábrán látható áramköri részleten ez azt jelenti, hogy :
I1R1+I5R5-Uf3+I4R4-Uf2+I3R3+I2R2+Uf1= 0.
Tényleges számoláskor ezt a törvényt úgy kell alkalmazni, hogy annyi zárt tetszõleges áramhurkot rajzolunk, hogy minden alkatrészen legalább egyszer átmenjen. Amikor ezt elértük, akkor további hurkokat nem érdemes létrehoznunk, hiszen ekkor már új független egyenletet nem kaphatunk. Az aktív elemeket is tetszés szerint, de egyöntetûen (mindegyiket egyirányúan, vagy a + ® -, vagy a - ® + módon) jelöljük.
Feladatok:
Az eddig tanultakat használjuk fel a következõ feladatok megoldásánál:
1./ Az Al. 9. ábrán látható kapcsolás a potenciométer formulát és a terheléskor bekövetkezõ jelnagyság (amplitúdó) változást segíti megértetni.
Kirchhoff huroktörvényét felhasználva az alábbi két egyenletet írhatjuk fel (Al. 13.) :
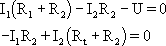
A második egyenletbõl
fejezzük ki az I1-et, és
helyettesítsük be az elsõ egyenletbe:
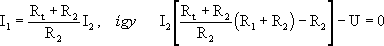 .
.
Mivel értelemszerûen az Uki = I2Rterh , ezért felírhatjuk az alábbi összefüggést:
![]() ,
,
átrendezve:
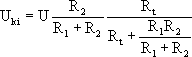 .
.
Bevezetve az : ![]() jelöléseket, átírhatjuk a fenti egyenletet az
alábbi alakra:
jelöléseket, átírhatjuk a fenti egyenletet az
alábbi alakra:
![]()
Ezt az összefüggést azonnal is megkaphatjuk, ha a Thevenin helyettesítõ tételt közvetlen alkalmazzuk (Al. 10. ábra):
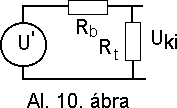
Az eredõ belsõ ellenállás :
![]()
A helyettesítõ feszültség forrás feszültsége :
![]()
Így az eredõ kimeneti feszültség :
![]()
Amint látjuk ugyanazt az összefüggést kaptuk, mint az elõzõ módszerrel, csak sokkal áttekinthetõbben és kevesebb számolási munkával.
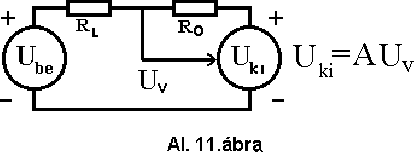
2./Egy másik példa : a vezérelt feszültségforrás. A mûködés alapja az, hogy az Uv vezérlõ
feszültség hatására Uki nagyságú kimeneti feszültség jön létre. Mekkora ez az Uv ?
Használjuk fel a szuperpozíció elvét. Ekkor ugyanis az Ube és Uki feszültségek hatását külön - külön kiszámolva elõjelhelyesen összeadhatjuk :
![]() .
.
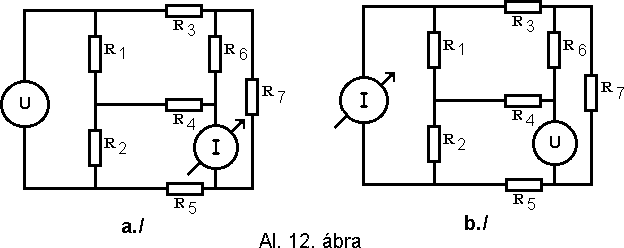
3./Feladat: bizonyítsuk be, hogy ha felcseréljük a feszültség generátort és az árammérõt (Al. 12. ábra a./ és b./), akkor a mûszeren mért áram értéke nem változik.
A számolás elõtt, - ha úgy könnyebb - adhatunk konkrét értékeket is az alkatrészeknek. Ilyen esetben gondoljuk meg azt is, hogy ha nem ideális a feszültséggenerátor, illetve az árammérõ (azaz nem nulla a belsõ ellenállásuk), akkor ez mekkora hibát okozhat, vagy a többi alkatrész értékéhez viszonyítva ez meddig hanyagolható el.
4./ A következõ néhány példa a gyakorlást segíti elõ:
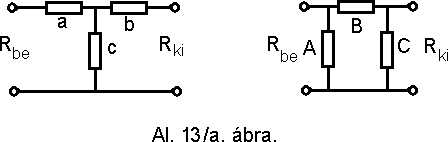
a./ Az Al. 13/a. ábrán látható két darab négypólus, amelyeknek számoljuk ki a bemeneti és kimeneti ellenállását. Ezután határozzuk meg az A, B, C ellenállást az a, b, c ismeretében illetve fordítva az A, B, C ismeretében számoljuk ki az a, b, c ellenállásokat.
b./ Az Al. 13/b. ábrán látható ellenálláslánc tagjainak száma tart a végtelenhez, próbáljuk meghatározni a bemeneti ellenállást, ha adottak az "a" és "b" értékei. Segítséget ad, ha észrevesszük, hogy milyen a matematikai törvényszerûség a lánc tagjai számainak növelésekor.
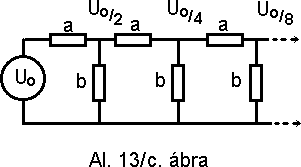
c./ Az Al. 13/c. ábrán a már ismert ellenállásláncot egy feszültség forrással tápláljuk. Kérdés mekkora legyen az "a" és "b" ellenállások értéke, hogy a csomópontokon a felírt értékek jelenjenek meg.
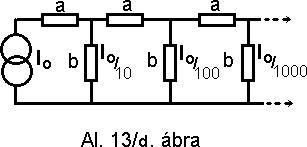
d./ Az elõzõ áramkört ezúttal áramgenerátorral tápláljuk, és arra keresünk választ, az "a" és "b" ellenállások függvényében, hogy mikor folynak a függõlegesen rajzolt tagokon a jelzett áramok.
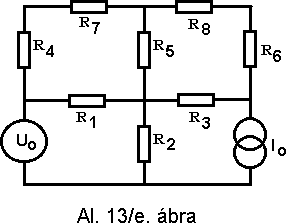
e./ A 13/e. ábrán látható áramkörön gyakorolhatjuk a reciprocitás és a szuperpozició elveit, valamint a Thevenin és Norton tételeket. A kimeneti feszültséget az R8-as ellenálláson mérjük.
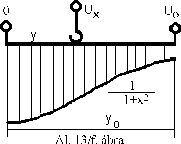
f./ A 13/f. ábrán potenciométert láthatunk: vékony, egymás mellé tekercselt szigetelt vezetékbôl áll, amivel egy csuszka teremt kontaktust. Ha a huzalszakaszok egyforma hosszúak lennének - pl. azért, mert párhuzamos szélû csíkra tekercselték ôket, - akkor a potenciométer "lineáris" lenne. Kérdés: milyen lesz az Ux = f (U0 , x) függvény, ha kontúrvonala az ábrán megadott jellegû függvény és x = y/y0 ?
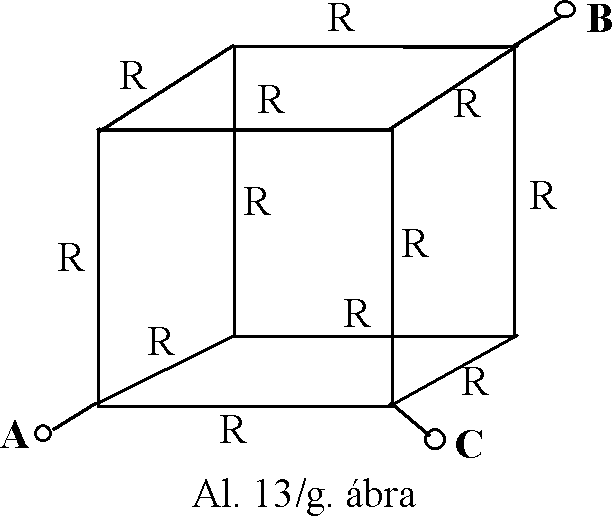
g./ A 13/g. ábrán egy olyan térbeli kocka látható, amelynek minden éle "R" ellenállású.
A feladat az, hogy meghatározzuk az A-B pontok (térátló), a B-C pontok (lapátló) és az A-C pontok (szomszéd csúcsok) közötti ellenállás értékét.
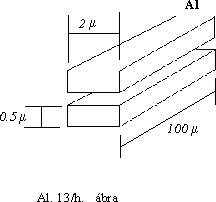
h./ A 13/h. ábrán egy chip két vezetéke látszik, amelyek alumíniumból készültek és szilicium-
oxid veszi körül ôket.
Határozzuk meg a vezetékek ellenállását, ha kontaktusok a legkisebb téglalapokhoz csatla-koznak, - valamint (közelítôleg) a közöttük lévô kapacitás értékét.
Mekkora ennek a rendszernek a felsô határfrekvenciája, illetve a mekkora a legrövidebb átvihetô jel szélessége?
(l. Bekapcsolási jelenségek fejezet.)