Az elektronika szerepe és jelentõsége

A bevezetõ részben azt szeretnénk hangsúlyozni, hogy miért fontos ez a tantárgy a nem kimondottan elektronikára specializálódott hallgatók (pl. temészettudományok majdani mûvelõi és oktatói stb.) számára. Azt szinte felesleges megemlíteni, hogy az egész világunk tele van az elektronika minden áldásával (számítógép, telefon, riasztók, tv, rádió, magnó, fax, mûhold, fûtõ-hûtõ-mosó-gyártó-vezérlõ elektronikák, robotok, stb). Emiatt egy mai átlagember sem lehet meg ilyen irányú minimális ismeretek nélkül, hiszen különben teljesen ki van szolgáltatva és csak passzív szereplõ lehet. Ekkor még nem tettünk említést arról, hogy az itt tanuló diákoknak kell majd továbbadni a természettudományos mûveltséget, tudást, illetve ezek szeretetét. Ez természetesen nem öncélú, hiszen a mának, és a jövõnek egyaránt nagy szüksége van és lesz az ilyen képzettségû szakemberekre is. Biztosan állíthatjuk, hogy annak az értelmiségnek, akinek nincs elegendõ ismerete az informatika (számítástechnika, elektronika, jelfeldolgozás stb.) megfelelõ területeirõl, annak a boldogulási esélye a saját szakmájában, - de meg merjük kockáztatni még a magánéletében is - sokkal kisebb lehet.

A tantárgy célja

Ennek az elõadás, tantermi gyakorlat és laboratóriumi foglalkozás-komplexumnak az az egyik célja, hogy megfelelõ magabiztosságot, jártasságot és gyakorlatot adjon az elektronika, a jelfeldolgozás, a hagyományos és komputeres méréstechnika területén. A másik "cél" a kollokvium, illetve informatika szigorlat sikeres elvégzése.

Ezt a szakterületet is csak úgy lehet jól mûvelni, ha megkedveljük, mert amihez nem értünk, abban nincs sikerélményünk, és attól elõbb, vagy utóbb elfordulunk.

Elvek, módszerek, képletek és pontosság

A fizikai tudományok kutatása megalapozta az elektronika elveinek fejlõdését is, ezért nem meglepõ, hogy az ebben követett alapvetõ gondolkodásmód nem különbözik lényegében a fizikában szokásostól (lásd pl. a mechanikai és egyéb analógiákat, modelleket), de a tudományok minden területén szükségszerûen fellépõ közelítések, elhanyagolások itt a gyakorlati igények miatt általában egy kissé eltérnek a fizikában megszokott indoklástól és mértéktõl.

Sokszor elõfordul, hogy a képletekbõl kapott eredményeket hajlamosak vagyunk abszolút pontosnak elfogadni, hiszen a " matematika nem téved ", mindig hibátlan. Ez igaz is, ha csak a számításokat nézzük, de nem szabad elfelejtenünk, hogy egy képlet születésekor mennyi egyszerûsítõ feltételt kell alkalmaznunk ahhoz, hogy az csak a természeti törvény lényeges paramétereit tartalmazza és ne legyen áttekinthetetlenül bonyolult a gyakorlat számára.

Az elõbbi bekezdéshez részletesebb magyarázat tartozik, mert egyébként félre lehet érteni, illetve magyarázni. Mint tudjuk a természeti jelenségeket leíró képletekhez alapvetõen két módon juthatunk el. Az elsõ módszernél a mérések után olyan modellt hozunk létre, amelyiknek mûködését már le tudjuk írni matematikai formulával, vagy a képlet - analógia alapján - más tudomány területrõl átörökölhetõ. Erre jó példa a mechanikai, és elektronikai oszcillációs jelenségek, ( valamint a rezonancia ) "meghökkentõ" hasonlósága. A második eljárásban széleskörû ismereteink, megérzés (intuíció), felismerés, továbbgondolás (extrapoláció), valamint feltételezés alapján új összefüggéseket írunk le, vagy a meglévõ képleteinket módosítjuk, bõvítjük ki. Vegyük észre, hogy mindkét esetben a kiindulás a tapasztalat, majd az összefüggés felismerése után a továbbgondolás, és ezután újra a valósággal való összevetés (kísérleti ellenõrzés).

Ahhoz viszont, hogy a képletek a lényeget tükrözzék, és áttekinthetõek, gyakorlatban használhatóak legyenek - kivételes esetektõl eltekintve - olyan tiszta körülményeknek, feltételeknek kell (kellene) lenni, amelyet csak ritka esetben tudunk biztosítani. Mindig arra törekszünk, hogy a valóságot minél pontosabban leíró összefüggéseket hozzunk létre, emiatt viszont sokszor a könnyû követhetõséget, kiszámíthatóságot, áttekinthetõséget "áldozzuk" fel. A fenti mondatokat három egyszerû példán szeretnénk illusztrálni.

Az elsõ példa a fizika (elektronika) egyik képlet-együttese a Maxwell egyenlet. Ezen összefüggések igen nagy pontossággal írják le az elektromágneses tér törvényeit, így alapvetõ érvényûek és univerzálisak, de ha a mérésben is elméleti pontosságot követelnénk meg, akkor igazán csak a vákuumban, illetve "végtelen" messze minden vezetõtõl, veszteséges rendszertõl alkalmazhatnánk. A gyakorlatban mégsem akkora a probléma, hiszen azt tapasztaljuk, hogy egészen jól mûködnek a fenti (és a belõlük levezetett) képletek alapján tervezett és megvalósított elektronikus berendezések.

A másik példa a szabadesés képlete. Az összefüggés igen egyszerû, persze csak ha vákuumban és homogén gravitációs térben vagyunk. Valóságos helyzetben többek között a légellenállást, annak sebességfüggését stb. kell figyelembe venni, de mint sejtjük, ekkor a kezdetben még egyszerû képlet jól elbonyolódik. Igaz, így sokkal pontosabban (van amikor erre van igény) írja le a valóságos folyamatokat.

A harmadik példa egy igazán egyszerû eset, nevezetesen amikor egyszerûen elgurítunk egy golyót egy sík felületen. A kezdeti energetikai feltételek teljes pontossággal adottak, mégis csak közelítõ pontossággal tudjuk megadni a golyó megállási koordinátáit. Az ok nyilvánvaló: a képlet nem tartalmazza (nem is tartalmazhatja) a felületi szabálytalanságokat és a golyó egyenetlenségeit, valamint az egyéb környezeti hatásokat. Viszont, ha ezeket a módosító hatásokat figyelembe tudnánk venni, akkor egy kismértékû pontosság javulásért cserébe egy sokkal bonyolultabb összefüggést kapnánk, így az eredmény kiszámolása is jelentõsen munkaigényesebb lenne.

A fentiekbõl igen fontos tanulságokat, és következtetéseket vonhatunk le, (általánosságban is) de ezt most már szigorúan csak az elektronikára korlátozzuk:

Minden mérési eredmény (néhány ritka esettõl eltekintve) legfeljebb annyira egyezhet meg az elméleti összefüggésbõl kiszámolttal, mint amennyire a képlet létrehozásánál feltételezett és a valóságos körülmények azonosak.

Ez a megállapítás természetesen nem meglepõ, de mégis sokszor értetlenül állunk, amikor a mérési adataink nem akarnak "tökéletesen" megegyezni az elméletbõl kiszámolttal.

Szükségesnek érezzük megjegyezni mit értünk a képlet és az ún. alapképlet fogalmán. Az értelmezõ szótár szerint a képlet: "betûkkel, számokkal, jelekkel kifejezett összefüggés", formailag a természeti törvény matematikai modellje. Az alapképleten azt az összefüggést értjük, amelyben csak az elsõ közelítésben fontos, legfõbb hatásokat vesszük figyelembe.

Ahhoz, hogy az elektronikában értelmesen és jó hatásfokkal tudjunk dolgozni az alábbi gondolatot érdemes megjegyezni:

Az alapképlet csak a domináns, uralkodó természeti törvényt, összefüggést tartalmazza, hiszen csak így tudjuk elõször a lényeget megérteni, követni. A kevésbé jelentõs hatásokat (perturbációkat), amelyek sokkal kisebb (sokszor nagyságrendekkel!) mértékben befolyásolják a rendszert, csak késõbb - a jelenség alapos megértése után - vesszük figyelembe.

A fenti megállapítást szemléletessé tehetjük egy egyszerû hasonlattal :

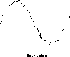
Mondjuk az alapképlet matematikai formája legyen egy szinuszfüggvény, amelynek az amplitúdója 1 volt. A nagyobb pontossághoz vegyünk figyelembe még egy kisebb hatást (a képlet bonyolódik); ez a hasonlatunkban legyen egy 0.1 voltos bármilyen jelalak, és a példa kedvéért legyen még egy sokkal kisebb harmadik hatás is (a képlet még tovább bonyolódik), amelynek mondjuk már csak 0.01 volt a nagysága. Ezeket összegezve kapunk egy nem egyenletes (perturbált, "rücskös") menetû - de jól felismerhetõ alakú - körülbelül egy voltos jelet. A Be. 1. ábrára nézve elõször a szinuszos forma dominál, tûnik ki (ez felel meg az alapképletnek), csak, ha finomítjuk a megfigyelésünket, akkor kezdjük észrevenni a képen a finomabb (másod-harmadrangú) részleteket is. Ez felel meg hasonlatunkban a precízebb, bonyolultabb képletnek.

A számítógép sokat segíthet, hiszen amíg fejben, papíron, táblánál általában csak az alapvetõ képletekkel, egyszerûsítõ körülményeket feltételezve tudunk követhetõen, áttekinthetõen és észszerû idõ alatt számításokat végezni, addig a számítógép bonyolultabb, de ezáltal sokkal pontosabb képlettel is elboldogulhat, legfeljebb hosszabb lesz a felhasznált gépidõ.

Figyelem! a számítógép nem helyettesítheti az emberi gondolkodást és ha számítógéppel dolgozunk, akkor is ismernünk kell az alapvetõ összefüggéseket, valamint a várható eredmény fõbb paramétereit (jelleg, dimenzió, nagyságrend), mert különben gyanú és kritika nélkül elfogadhatunk bármilyen, esetleg teljesen értelmetlen adathalmazt is jó eredményként!

Legtöbbször elõre el kell döntenünk, hogy melyik képlettel, illetve számítási módszerrel akarunk dolgozni. A döntés alapja, hogy a majd megkapott eredményünknek milyen pontossági követelménynek kell megfelelnie. A tisztán elvi számolásoknál elképzelhetõ "bármilyen" pontosság, de a valóságos áramkörök megoldásánál sokszor megelégszünk az 1-10% precizitással is! Miért van ez így? Erre is nézzünk egy rendkívül egyszerû példát, az Ohm törvény alkalmazási körébõl:

Az Ohm törvény alapvetõ összefüggést fejez ki. A gyakran használatos képletben azonban nincs benne az anyag inhomogenitása, hõfüggése, általában semmilyen függése a környezeti paraméterektõl, és nincsenek figyelembe véve idõben változó jelnél, a parazita komponensek (induktív, kapacitív), illetve az alkatrészek zaja, idõbeli stabilitása, értékének hibája, szórása. A felsorolás ijesztõnek tûnik, de elõzõ bekezdésekben elmondottak alapján már sejtjük, hogy ezek a hatások általában (de nem mindig) egy vagy több nagyságrenddel kisebbek, mint maga a csupasz Ohm törvény.

Vigyázat! A fenti példát felhasználva lehetnek olyan körülmények, amikor az úgynevezett mellékhatások elérhetik, sõt meg is haladhatják az alapképlet következményeit. Ilyen eset pl. amikor nagy hõfüggésû anyagot szélsõséges hõmérsékleti viszonyok között , vagy egy egyszerû ellenállást igen magas (»GHz) frekvencián használunk. Ekkor az eddig jelentéktelennek, elhanyagolhatónak kezelt hatások már meghaladhatják a kiinduláskor elfogadott összefüggésbõl kiszámítható értéket!

Soha sem a képlet a "hibás"! Esetleg nem a megfelelõt használtuk, vagy a képlet feltételei nem teljesülnek, illetve az áramkört felépítõ elemek paramétereit (illetve ezek függését) nem jól mértük fel.

Összefoglalva: az elektronikában (igaz másutt is) - különösen az áramkörök jellemzõinek kiszámításánál - csak akkor tudunk megfelelõen dolgozni, ha felismerjük, hogy mi a lényeges folyamat (a hozzá tartozó képlettel) és mik azok, amik csak kis hatásúak és mintegy csak kicsipkézik a fõ mûködést és ezáltal sokszor elhanyagolhatóak.

Általában azt is mondhatjuk, hogy a tudományokban való jártasság nem más mint - nyilvánvalóan az alapvetõ törvények és összefüggések ismeretén kívül - az értelmes, indokolt és a szakmailag jogos elhanyagolások tudománya!

Vannak egyéb - a gyakorlatban jól használható - elvek, módszerek, szokások, feltételezések, amelyek alkalmazása sokat segíthet, és így jelentõsen megkönnyítheti a megértést, valamint a számítások elvégzését. Ezek közül a következõ részben a teljesség igénye nélkül, mintegy ismerkedésképpen, elõzetes összefoglaló áttekintés miatt, néhányat felsorolunk, és azoknál, ahol ezt szükségesnek tartjuk a késõbbi fejezetekben részletesebb magyarázatot is adunk.

1./ Földpont: A földgolyó egy nagy felületû vezetõ gömb, emiatt rajta a statisztikus töltésmennyiség változások kiátlagolódva nem okoznak jelentõs potenciál változást. Ez a tulajdonság teszi lehetõvé, hogy aránylag zavarmentes referencia pontként, stabil alapként használjuk.

Esetenként, amikor a tényleges földpont használata nem lehetséges, akkor az ún. közös nullát alkalmazzuk erre a célra. Ez legtöbbször a tápegység egyik pólusa, amihez sokszor az áramkör dobozát, árnyékolását, szûrõkondenzátorok közös pontjait hozzákötjük.

2./ Aktív és passzív elemek: Ebbõl a szempontból az áramköri alkatrészek legtöbbször

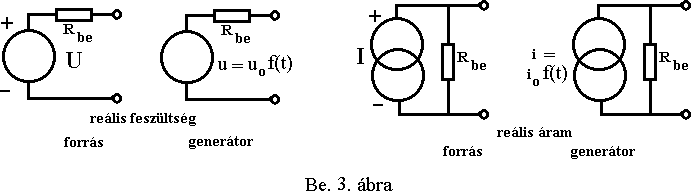
- de nem mindig - jól elkülöníthetõek, hiszen amelyik elem ún. külsõ táplálás nélkül feszültséget, vagy áramot hoz létre (termel), azt aktív elemnek, amelyik nem, azt passzívnak nevezzük. Az utóbbira példa többek között az ellenállás, kondenzátor, induktivitás, dióda, tranzisztor stb. Aktív alkatrészek a feszültség és áram források, illetve generátorok. Általában szokás az egyen jeleket szolgáltatókat forrásoknak és az idõben változókat generátoroknak nevezni. Megkülönböztetünk még ideális és reális (valóságos) forrásokat illetve generátorokat. (Be. 2. és 3. ábrák). Ezekrõl részletesebb leírást találhatunk az 5./-ban.

Az alábbi ábrán néhány a késõbbiekben sokat használt szimbólum látható:

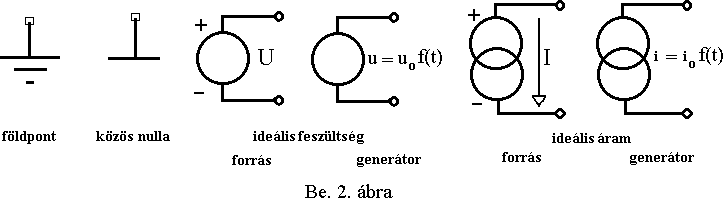
Kérdés: a fényelem világosban és sötétben, illetve a tekercs állandó és változó mágneses térben aktív, vagy passzív elemnek tekintendõ?

3./ Mérési pontok értelmezése: Amikor egyszerûen azt kérdezzük, (vagy kijelentjük) hogy egy áramköri ponton mekkora feszültség van, akkor mindig a föld (vagy a közös 0) vezetékhez képest kell ezt értenünk. Amikor egy alkatrész, vagy áramkör két kijelölt pontja közötti feszültségre vagyunk kíváncsiak, akkor ezt határozottan ki kell jelentenünk!

4./ Jelek nagyságát abszolút és relatív nézõpontból vizsgálhatjuk:

Az elsõ esethez a nagyságrendeket - emlékeztetõül - a következõ sorokban foglaljuk össze:

Azt eldönteni, hogy egy jel "kicsi", vagy "nagy" csak az áramkör tervezési, méretezési adataiból és az un. normális mûködési paramétereibõl lehet. Igaz ezt is csak nagyságrendi közelítéssel tudjuk megtenni. Erre jó példa az, hogy amíg egy mûholdvevõ bemenetén már a mikrovolt is nagy jelnek számít, addig egy gyorsítóban a többezer Volt is sokszor jelentéktelen érték lehet.

A második esetnél csak a jelek nagyságát viszonyítjuk egymáshoz, azaz egy arányszámot számítunk ki. Ezt a számot nagyon sokszor használjuk, hiszen egy áramkörre igen jellemzõ a be és kimenete közötti változás viszonyszáma: az átvitel. (Ha ez az érték nagyobb mint egy, akkor erõsítésrõl, ha kisebb, akkor gyengítésrõl beszélhetünk.)

Ezek a viszonyszámok sok nagyságrendet is átfoghatnak, ezért célszerûbb ezek logaritmusával számolni. Sorbakapcsolt hálózatok esetén az egyes fokozatok erõsítéseinek viszonyszámai összeszorzódnak, de a logaritmusaik "csak" összeadódnak, ami sokkal egyszerûbb és fejben is könnyebben elvégezhetõ. Ezután nézzük meg a decibel - mint egység - definícióját:

Feszültség és áramviszonyra:

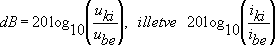
Teljesítmény () viszonyra:

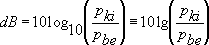
A "be" helyett sokszor írunk etalon, vagy referencia jelet az indexbe, amikor is egy meghatározott alapjelhez képest viszonyítjuk a jelünket. A feszültség (vagy áram, illetve teljesítmény) arányt képezhetjük akár az abszolút, akár a csúcs, vagy effektív értékekre is.

Nézzünk meg néhány jellegzetes, megjegyzésre érdemes arányszámot:

(az elsõ sorban az arányszámokat írtuk, a második sor a feszültség és áram, míg a harmadik sor a teljesítmény viszonyt mutatja decibelben.)

arány: 100 10 2 1 1/2 1/ 1/10

---------------------------------------------------

dBu,i : 40 20 10 6 3 0 -6 -3 -20

dBp 20 10 5 3 1.5 0 -3 -1.5 -10

Látszik a táblázatból, hogy a -3dB-nek kitüntetett szerepe van, hiszen ilyenkor a teljesítmény a felére , (a feszültségek és áramok -ed részükre) csökkenek. Errõl a témáról részletesebb leírást a "Transzfer karakterisztikák" címû fejezetben találhatjuk meg.

Az elektronikus alkatrészek döntõ része (ezáltal a belõlük felépített áramkörök szintén), - mivel tartalmaznak valamekkora ellenállást - a természeti törvényekbõl következõen kikerülhetetlenül zajt hoznak létre. Az áramkörök adottságaitól függõen a zaj amplitúdója nagyon sok nagyságrendet átfoghat (általában: kb. pikovolt-millivolt). Azokban az áramkörökben, ahol nem tekinthetünk el a meglévõ zajtól, ott legtöbbször decibelben adjuk meg az ún. jel/zaj viszonyszámot.

5./ Belsõ ellenállás: A feszültség és jelforrásoknál (tápláló, meghajtó és vezérlõ generátoroknál, valamint a vezetékeknél), - ha nem adunk meg más adatot - akkor, "elsõ közelítésben" mindig nulla belsõ ellenállást, tételezünk fel, vagyis különbözõ terhelésnél nem változhat a feszültsége. Definíciószerûen az elvi kapcsolásokban szereplõ feszültségforrás belsõ ellenállása mindig nulla, az áramforrásé pedig mindig végtelen. ezeket nevezzük ideális forrásoknak, generátoroknak ( Be. 2. ábra ).

A valóságban a feszültség forrásokra és generátorokra ez az érték természetesen nulla nem, hanem csak az átlagosan szokásos értékekhez képest "nagyon kicsi" lehet!

Szimbólumaik a Be. 3. ábrán láthatóak:

6./ A függetlenség elve: Ez azt jelenti, hogy két áramkör, vagy áramköri részlet nincs egymásra hatással, vagyis függetlenül tudjuk õket kiszámolni, ha az elsõ kimeneti ellenállása, impedanciája jelentõsen kisebb (<1-10%-a) mint a rákötött, terhelõ áramkör bemeneti ellenállása, impedanciája. Ez sokszor rendkívül nagy mértékben leegyszerûsítheti a megértést, és különösen a számolást. Ez a módszer akkor mûködne ideálisan (hibátlanul), ha a kimeneti ellenállás nulla és a bemeneti ellenállás végtelen lenne, azt viszont tudjuk, hogy csak elméletileg létezhet nulla, vagy végtelen nagy ellenállás, impedancia. Elvileg nulla belsõ ellenállásúnak tekintjük a feszültségforrást, az árammérõt és a vezetéket és elvileg végtelen belsõ ellenállásúnak az áramforrást, a feszültségmérõt és a szigetelõt. A valóságban ezeket a nulla és végtelen értékeket csak megközelíteni tudjuk.

Néhány gyakorlati adat: A vezetékek ellenállása kisebb lehet, mint ezredohm (mohm), az akkumulátor és az árammérõ belsõ ellenállása, mint századohm, az elektromos hálózat ellenállása, mint egy ohm.

A feszültségmérõk (és áramgenerátorok) ellenállása nagyobb lehet, mint 10-100 megaohm (Mohm), szigetelések ellenállása elérheti a teraohmot (1012 ohm).

7./ Ideális és koncentrált paraméterû alkatrészek: A valóságos elektronikus alkatrészek (pl. az ellenállás, a vezeték, a kondenzátor, a tekercs, stb.) tulajdonsága, hogy mindegyike tartalmazhat ellenállást, kapacitást, és induktivitást. Mi ennek ellenére, amit "R"-nek jelölünk, azt tisztán ellenállásnak, amit "C"-nek, azt tisztán kondenzátornak, amit "L"-nek, azt tisztán induktivitásnak tekintjük.

(A valóságos alkatrészek elõbb említett ún. parazita adatait, ha szükséges pl. a vezetékek ellenállását, kapacitását, induktivitását beleérthetjük, beleszámíthatjuk az illetõ R, C, L alkatrészekbe.)

Ezt mi koncentrált paraméterû módszernek nevezzük.

Az ellenállásoknál (bár a kiviteltõl erõsen függõen pl. hogy tekercselt, köszörült, tömör, vagy SMD) elég magas frekvenciáig (MHz-GHz) általában nem kell a szórt paramétereket figyelembe venni. Az SMD (surface mounted : felület szerelt) azt jelenti, hogy az alkatrészeknek nincs kivezetése, hanem közvetlenül a felületre vannak forrasztva.

A kondenzátorok parazita ellenállását, amely a hozzávezetési soros és az átvezetési párhuzamos ellenállásból áll, néhány ritka esettõl eltekintve (ilyen pl. egy rossz-minõségû elektrolit kondenzátor) általában nem kell figyelembe venni. Az induktivitásától - különösen tekercselt kivitel esetén - néhány MHz felett már nem tekinthetünk el. Itt is jó értelemben kivétel az SMD technológia.

Az induktivitás az, aminek szinte soha nem hanyagolhatjuk el az ellenállását (hiszen a huzalnak mindig van), és meneteinek egymáshoz, illetve a külsõ környezethez képest is jelentõs lehet a kapacitása.

(Az induktivitásra azt is mondhatjuk, hogy az tulajdonképpen egy - a saját és külsõ ellenállásától függõ minõségû - rezgõkör, de ha körültekintõen méretezzük és megfelelõ frekvenciatartományban használjuk, akkor ez a tulajdonság nem lesz igazán zavaró.)

Kiegészítésként felhívjuk a figyelmet arra az - egyébként közismert - tényre , hogy mivel minden alkatrésznek van felülete, ezért - a környezetéhez képest - van ún. "szórt" kapacitása is. Ebbõl viszont az következik, hogy minden elektronikai eszköznek (és kapcsolásnak) lesz felsõ határfrekvenciája. Ez a késõbbiekben megtanulandó integráló hatás egyik következménye (lásd: "alaptörvények" fejezetben az "impedancia" címû alfejezetet).

8./ Linearitás: Lineáris alkatelem, vagy áramkör az, amelyre többek között az is igaz, hogy az áramok és feszültségek kapcsolatát lineáris egyenletek fejezik ki. Egyszerûbben fogalmazva ez azt jelenti, hogy n-szer akkora feszültség hatására n-szer akkora áram folyik. Természetesen az összefüggésnek fordítva is igaznak kell lennie, azaz:

ha, egy áramkörön átfolyó i1 áram hatására u1,

illetve az i2 áram hatására u2 feszültség jelenik meg,

akkor i1 + i2 áramnál, a feszültség u1 + u2 nagyság lesz.

A már említett R, L, C elemekre mondhatjuk, hogy ilyenek, hiszen ha az ellenállás, az induktivitás és a kapacitás értéke nem függ a rákapcsolt feszültségtõl (vagy átfolyó áramtól), akkor teljesül ez a feltétel.

A Be. 4. ábrán láthatjuk a három említett ideális alkatrésznek az alapképleteit:

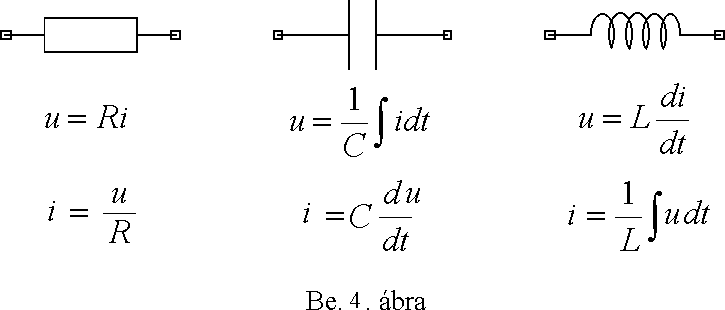
Általában igaz, hogy lineárisak az olyan áramkörök, amelyekben a már említett alkatrészeken kívül csak források és generátorok vannak. Késõbb azt is látni fogjuk, ha nem lineáris alkatrészeket (pl. félvezetõket) használunk, akkor is, bizonyos körülmények között pl. megfelelõen kis jelekkel és nagy körültekintéssel dolgozva, igaz ritkán, de alkalmazhatjuk a lineáris egyenleteket (Inhomogén linearitást, a differenciális ellenállást és a "h" paramétereket a félvezetõ modellekrõl szóló fejezetben találhatjuk meg).

9./ Reciprocitás elve: a gyakorlatban és lineáris áramkörökben, azt jelenti, hogy egy feszültséggenerátor és egy árammérõ helye egymással felcserélhetõ, miközben az árammérõ ugyanakkora áramértéket fog mutatni. Hasonlóan egy áramgenerátor , és egy feszültségmérõ helye is egymással felcserélhetõ, de ekkor természetesen a mért feszültség lesz azonos! Mindkét esetnél alapvetõ feltétel, hogy az áramkörben egyetlen generátor lehet, és a felcserélt eszközök belsõ ellenállása azonos kell, hogy legyen. ( Be. 5. ábra)

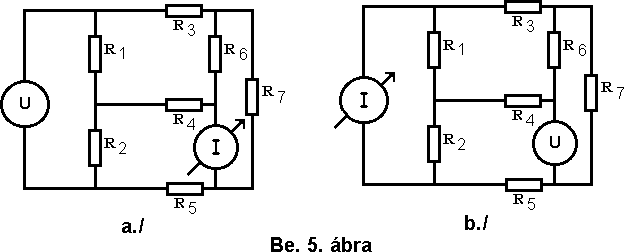
Az elmondottak alapján az állítás az, hogy az a./ és a b./ bekötés mellett az árammérõn mutatott érték azonos lesz.

Ennek bizonyítása és ezzel kapcsolatos példák megadása a következõ (Alaptörvények címû) fejezet feladata lesz.

10./ A szuperpozíció elve: azt jelenti, hogy ha a linearitási feltételek biztosítva vannak, és több feszültséggenerátor van az áramkörben, akkor egy tetszõleges ágban az áramot úgy számolhatjuk ki, hogy minden egyesforrásfeszültség okozta áramot külön - külön meghatározva, egyszerûen elõjel-helyesen összeadunk. Ilyenkor az éppen nem számolt generátorokat nulla feszültségûnek tekintve, a saját belsõ ellenállásukkal helyettesítjük.

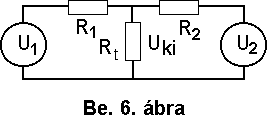
A szuperpozíció elve azt állítja, hogy az Rt -n átfolyó áramot úgy számolhatjuk ki, hogy egymástól függetlenül pl. elõször az U1 hatására, majd az U2 hatására létrejövõ áramokat elõjelhelyesen összeadjuk. A következõ (Alaptörvények címû) fejezetben ezt bizonyítani fogjuk és ott találunk megoldandó példákat is.

11./ A pontosság határai: Az elõzõ oldalakon ezzel már elvi szinten foglalkoztunk, de mivel a gondolatmenet lehet, hogy elég szokatlan, ezért egy más szemszögbõl, példákon keresztül igyekszünk ezt megvilágítani. Az is elõfordul, hogy az elvi és gyakorlati megközelítések egymásnak látszólag ellentmondanak.

Elsõ példa: Egy áramkörben a keresett értékek (feszültségek, áramok) elvi kiszámolásánál - mivel ekkor az alkatelemek értékeit "teljesen precíznek" tételezzük fel - a pontosság csak ésszerûség kérdése. Ilyenkor, ha eléggé indokolt, akár 3 - 6 számjegyig is elmehetünk. A valóságos áramkörök számításánál azonban, nagyon meg kell gondolnunk, hogy van-e értelme a több mint 2 -3 számjegynyi pontosságnak, hiszen a tényleges alkatelemek paramétereinek szórása általában 1 - 10%.

Megjegyzés: gyártanak 0.1% - os pontosságú alkatrészt (pl.ellenállást) is, de ugyanakkor vannak több száz %-os szórású (pl. kondenzátorok, félvezetõk) alkatelemek is.

Második példa: Tételezzük fel, hogy jól ismerjük egy áramkör mûködését, mert megtalálták (és igazolták) hozzá a megfelelõ modellt és ezáltal a matematikai összefüggés (képlet) is adott. Mondjuk azt a példa kedvéért, hogy ebben az áramkörben egy exponenciális kisülési (vagy töltõdési) jelenség játszódik le. Elméletbõl jól tudjuk, hogy ez a görbe soha nem érheti el azt a határértéket amihez tart, csak közelít hozzá (limes), ezért azt kell mondanunk, hogy ez a folyamat a végtelenségig tart! Mennyire igaz ez a valóságban? Anélkül, hogy filozófiai mélységû vitákba bonyolódnánk, gondoljuk meg, hogy amikor már egyéb jelek (pl. a zaj) már akár több nagyságrenddel nagyobb, mint a különbség a határérték és a tényleges jel között, akkor van-e értelme kijelenteni azt, hogy a folyamat még nem fejezõdött be? Erre azt kell válaszolnunk, hogy igenis, meg nem is. A felelet attól függ, hogy teljesen elvi oldalról nézzük, vagy a realitás valóságában vizsgáljuk a folyamatot.

Tudjuk az elméleti válasz a "soha", míg a valóságban azt kell mondanunk, hogy ha a közelítés hibája már kisebb, mint pl. 1 - 10% (attól függõen, hogy milyen a pontossági igényünk), akkor a folyamat részünkre gyakorlatilag " befejezõdött"!

Megjegyzés: Az igazsághoz tartozik, hogy a jelfeldolgozási elmélet és a gyakorlati technika állandó fejlõdésével az ún. kimutatható jelek nagysága folytonosan kisebb lesz. Az ûrszondák rádióadásainál elõfordul, hogy a zaj akár 10 - 20 nagyságrenddel nagyobb, mint a hasznos jel és mégis hasznosítható adatot, képet tudunk belõle kinyerni!! Igaz ezek az eljárások és technikák (korreláció, sokszoros lejátszás stb.) általában igen bonyolultak, hosszadalmasak és költségesek.