Mese a tranzisztor fogantatásáról és születésérôl.....

A félvezetôtechnika kifejlôdését - mint annyi sok másét - a második világháború provokálta. A lokátor-(radar)-technikai fölény megszerzése ugyanis élet-halál kérdése volt. A szövetséges erôk már egy jelentôs gyôzelmet tudtak maguk mögött: a magnetron felfedezésével ôk voltak a mikrohullámok urai. - De ezeknek a hullámoknak a detektálását egy obskúrus, tisztázatlan hátterû technikával elôállított aprócska eszközre, az ún. mikrohullámú diódára bízták. Ezek a "közönséges" diódákra hasonlítottak, de még mikrohullámokon is mûködtek.

Élenjáró laboratóriumok végeztek prominens fizikusok által vezetett munkát lényegében a félvezetôk elôállítására. Ezzel párhuzamosan haladt a szilárdtestek elméletének kutatása, felfedezése. - A negyvenes évek végére kialakult "gyártási" technológia mai szemmel ugyancsak kezdetlegesnek tûnik: az egykristályok foszfor-szennyezettségi mértékét egy kifinomult orrú technikus szaglása alapján állapították meg...

Az amerikai Bell laboratóriumban dolgozó csapatnak 1947 karácsonyára sikerült elôállítania egy félvezetô alapú vezérelhetô elemet, amelyet nem nagyon szerencsésen tranzisztornak kereszteltek el. A felfedezés technológiai háttere mai szemmel eléggé furcsa volt: egy aprócska vízcseppet is el kellett helyezni a félvezetôhöz csatlakozó tûcskék közé. - Az számított igazi diadalnak, amikor ezzel az eszközzel sikerült oszcillátort létrehozni. - Tûs tranzisztorokat ma már nem gyártanak.

A tranzisztor felfedezéséért Bardeen, Brattain és Shockley 1956-ben Nobel díjat kapott. (Bardain késôbb újabb Nobel díj részese lett. ) - Pontosabban az kell mondanunk, hogy az elsô két személy nevéhez fûzôdik az ún. tûs tranzisztor elôállítása. Shockley csak azért került a díjra jelöltek közé, mert neki volt egy elmélete egy lehetséges tranzisztorról, amelyet azonban - akkor - nem tudott kísérletileg igazolni. Ennek is eljött az ideje: az ún. térvezérlésû tranzisztor ötlete, elmélete, elsô elôállítása egyértelmûen az ô nevéhez fûzôdik. Ez a tranzisztor teszi lehetôvé napjaink igen fejlett és igen olcsó komputer-technikáját.

Nagyon fontos azt átlátni, hogy a félvezetôtechnika egészen egyedülálló abban, hogy még elemi jelenség szinten sem mûvelhetô jól-rosszul felszerelt iskolai szertárakban, vagy odahaza a konyhaasztalon. (Kuktafazékban nem lehet egykristály növeszteni!) Ezért nem szerepelnek ilyen jellegû kísérletek a népszerû fizika könyvekben, ezért nem található semmi ilyen jellegû leírás vagy kísérlet Öveges kitûnô könyveiben sem. Hétköznapi körülmények között - bármekkora technikai zsenialitás mellett - sem lehet egy jó, vagy akár csak mûködôképes tranzisztort elôállítani. A tranzisztorok, sôt az integrált áramkörök gyártása rendkívül költséges berendezéseket és kíméletlenül betartandó precíziós technológiákat igényel. Nem véletlen, hogy Magyarország a félvezetô gyártásban eleddig nem jeleskedett.

A félvezetõk fizikai alapjai

A félvezetõk elméletét a szilárdtestfizika tárgyalja, (ezt a tantárgyat csak néhány év múlva tanulják). Most egy egyszerû, áttekinthetõ, szemléletes - tehát pontatlan - modellt mutatunk be, amely a minimális alapokat érinti a szilárd testek sávszerkezetében.

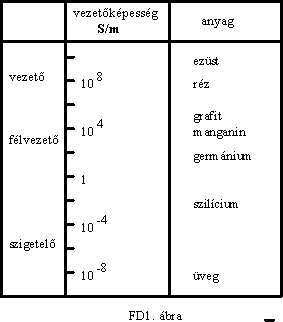
A szilárd anyagokat szobahõmérsékleten mérhetõ vezetõképességük alapján vezetõkre, szigetelõkre és félvezetõkre osztjuk.

A vezetõkre a 105 - 109 S/m, a szigetelõkre pedig a 10-4 - 10-10 S/m vezetõképesség jellemzõ.

A félvezetõk vezetõképessége e két tartomány közé esik. (pl. Si, Ge, Se). (FD1.ábra)

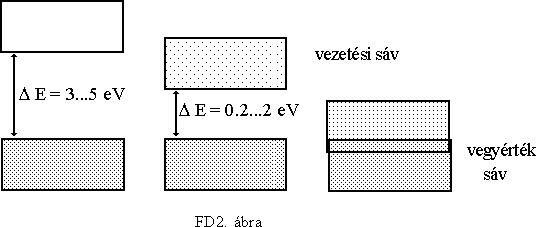
Az eltérõ vezetõképességek a sávmodellel magyarázhatók. Az atommag körül keringõ elektronok csak pontosan meghatározott pályákon tartózkodhatnak és ennek megfelelõ energiákat vehetnek fel. Az anyag vezetési tulajdonságai szempontjából csak a legkülsõ elektronoknak, a vegyérték-elektronoknak van szerepük. A kristályos szilárd anyagban az egyes atomtörzsek elektronfelhõinek átfedése hatására az elektron-energiaszintek sávokká szélesednek ki, így alakul ki a vegyérték-sáv és a vezetési sáv. Az egyes sávokat ú.n. tiltott sáv választja el egymástól, ennek megfelelõ állapotban elektron nem létezhet. A vegyértéksáv be van töltve elektronnal, így ez a sáv vezetést nem hozhat létre. A vezetési sávba került elektronok a külsõ tér hatására szabadon elmozdulhatnak és így elektromos áram jöhet létre. Ahhoz, hogy az elektronok a vegyértéksávból a vezetési sávba juthassanak, akkora energiával kell rendelkezniük, amely elég a tiltott sáv átugrásához. Ezt az energiát pl. a hõmérséklet biztosíthatja (E » kT). A tiltott sáv szélessége szabja meg, hogy adott hõmérsékleten (pl. szobahõmérsékleten) egy anyag a vezetõk, félvezetõk vagy szigetelõk csoportjába tartozik-e? (FD2.ábra) Vezetõknél ezek a sávok részben átfedik egymást, úgyhogy a legnagyobb energiájú elektronok szabad elektronként jelentõs vezetõképességet eredményeznek. Ezzel szemben a szigetelõknél olyan széles a tiltott sáv, hogy elektronok nem juthatnak a vezetési sávba. Megfelelõen magas hõmérsékleten néhány kerámia szigetelõ vezetni kezd, mert a hõmérsékleti gerjesztés elég nagy a tiltott sáv átlépésére. Abszolút nulla fok közelében a félvezetõk is szigetelõként viselkednek, csak akkor válnak vezetõvé, ha valamilyen formában a tiltott sáv átlépéséhez elegendõ energiát közlünk a vegyértéksáv elektronjaival. Az ûrhajókban is biztosítani kell a megfelelõ (szobahõmérséklet körüli) környezetet, mert a tranzisztorok "befagyhatnak".

Szobahõmérsékleten már olyan "sok" elektron jut fel a vezetési sávba, hogy a félvezetõk elérik az 1. ábra szerinti vezetõképességet. (A tiltott sáv szélessége Si-nál 1,2 eV, Ge esetén 0,72 eV, a hõmérsékleti gerjesztés energiája, kT » 0.025 eV).

Kristályszerkezet

A félvezetõ kristály felépítését a Si-on mutatjuk be. A Si rácsa a gyémántrácshoz hasonló, minden Si atomnak négy közvetlen szomszédja van. A vegyértéksávban négy valenciaelektron található, ezek kovalens kötéssel alakítják ki a kristályrácsot. A tökéletes rácsszerkezethez igen nagy tisztaságú félvezetõ alapanyag szükséges, 1010 darab Si atomra legfeljebb 1 idegen (szennyezõ) atom juthat. Ez azt jelenti, hogy egy kb. 1000 atomtávolságnyi élû kocka közepén egy idegen atom van.

A tiszta félvezetõ kristályban abszolút nulla fok közelében minden elektron energiája a tiltott sáv alatt van. A vezetési sáv üres, a vegyérték sáv tele van, a kristály áramot nem vezet (szigetelõ). A hõmérsékletet növelve elektronok gerjesztõdnek a tiltott sávon át a vezetési sávba, amelyek vezetést hoznak létre a kristályban. A vezetésben nem csak a vezetési sávba jutott szabad elektronok vesznek részt, hanem a vegyértéksávban a helyükön keletkezett elektronhiány, vagy más szóval lyuk, mint pozitív töltés szintén részt vesz a vezetési folyamatban. A különbözõ elõjelû töltések természetesen ellenkezõ irányban mozognak a külsõ tér hatására. A lyuk, azaz elektronhiány oly módon mozog, hogy az elektron a térerõsség hatására az elektronhiány helyét (a lyukat) betölti, és így az elektronhiány (lyuk) arra a helyre kerül, ahol azelõtt volt az elektron. A hõmérsékleti gerjesztés hatására létrejövõ elektron-lyuk párok hatására létrejött vezetést nevezzük sajátvezetésnek. (FD3.ábra)

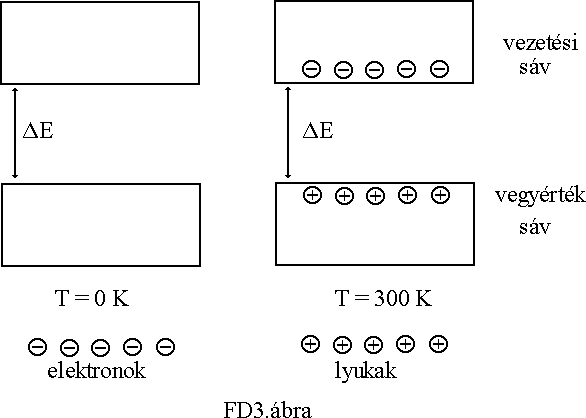
A sajátvezetés, azaz az elektron - lyuk párképzõdés nemcsak hõmérsékleti gerjesztés hatására jöhet létre, a gerjesztéshez szükséges energiát pl. elektromágneses sugárzás (fény), sõt elemi részecskék sugárzása is elõidézheti. Az energiaközlés hatására felbomló kötések következtében a töltéshordozók elemi részecskéi, (egy elektron és egy lyuk,) mindig párosan keletkeznek. Természetesen ennek a folyamatnak a fordítottja is folyamatosan jelen van, azaz az elektronok visszatérnek a vezetési sávba, és ott ez a lyukak megszûnését jelenti. Ezt a folyamatot nevezzük rekombinációnak. Állandó hõmérsékleten a párképzõdés és a rekombináció egyensúlyban van, szobahõmérsékleten 1 cm3 Si kristályban, amely 1023 atomot tartalmaz, kb. 2 1010 elektron és lyuk van. Ha a hõmérsékleti gerjesztés energiája eléri a tiltott sáv átlépéséhez szükséges értéket, sajátvezetés meredeken nõni kezd, majd akkor telítõdik, ha a párképzõdés és a rekombináció egyensúlyba kerül.

Szennyezés hatása

Ha a félvezetõ kristályba idegen atomokat juttatunk, a vezetõképesség jelentõsen nõhet. Elsõsorban olyan szennyezõ atomok jönnek szóba, amelyek külsõ elektronhéján eggyel több vagy kevesebb vegyértékelektron van, mint a kristály atomjainak, tehát 5 vagy 3 elektron. Ilyenek pl. az As ötvegyértékû (arzén) vagy a háromvegyértékû In (indium).

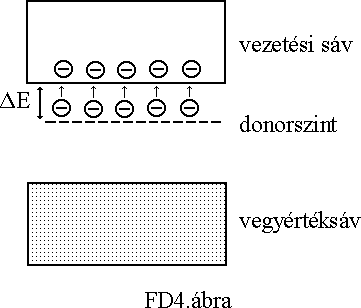
Ha az 5 vegyértékelektronnal rendelkezõ As-t helyezzük el a Si kristályrácsába, a kristály felépítéséhez az ötödik elektronra nincs szükség, ezért nagyon kis energiaközlés hatására szabad elektronná válik, és a vezetési sávba jut. (A donor szint és a vezetési sáv közti tiltott sáv szélessége D  E @  0.1 eV). A sávmodellben a szennyezõ atomok energiaszintje a vegyérték és a vezetési sáv között helyezkedik el, így már szobahõmérsékleten elegendõ az energia arra, hogy az ötödik elektronok jelentõs része a vezetési sávba jusson, mivel a hõmérsékleti gerjesztés kT nagyságrendû energiája közel ugyanekkora. Ezáltal a szilíciumkristály vezetõképessége erõsen megnõ. A vezetési sávban a szennyezõ atomok számának megfelelõ elektron van, ennél lényegesen kisebb a sajátvezetésnek megfelelõ elektron - lyuk pár. Mivel sok az elektronok száma, a rekombináció lehetõsége megnõ, így a lyukak száma erõsen lecsökken. A vezetést szinte kizárólag elektronok okozzák. Az ilyen kristályt nevezzük n típusú félvezetõnek. A hozzáadott szennyezõt, mivel plusz elektront adott le a kristálynak, donoratomnak nevezzük. A kristályban azonos számú pozitív töltés van a rácsionokban, mint ahány szabad elektron a kristályban, ezért természetesen az anyag elektromosan semleges.

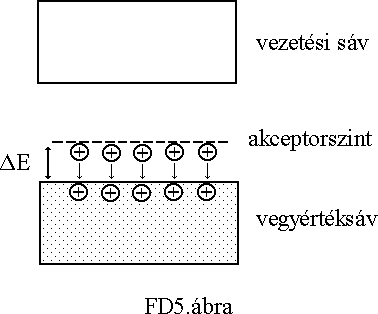
Ha a 3 vegyértékelektronnal rendelkezõ In-al szennyezzük a Si kristályt, akkor a kötéshez szükséges elektront a szomszédos Si atom adja, és ott a kristályban elektronhiány, lyuk keletkezik. Ezeket a lyukakat további szomszédos elektronok tölthetik be, és így a lyukak szabad vándorlása jöhet létre, azaz elektromos áram folyik külsõ tér hatására a kristályban, ahol a töltéshordozók pozitív töltésû lyukak. (FD5.ábra) Az ilyen félvezetõkristályt p típusúnak, a három vegyértékû szennyezõatomot, mivel egy elektront köt le, akceptoratomnak nevezzük. Természetesen a p típusú félvezetõ is elektromosan semleges anyag. Minden akceptoratom negatív töltésû ionná válik a felvett elektron által, amellyel szemben egy szabadon mozgó lyuk található a kristályrácsban.

A szennyezett félvezetõkben a szennyezõ atomok hatására létrejött elektronokat ill. lyukakat többségi töltéshordozóknak nevezzük, míg a sokkal kisebb számban jelen lévõ, sajátvezetést okozó lyukak ill. elektronok a kisebbségi töltéshordozók. A p típusú félvezetõben tehát a lyukak a többségi és az elektronok a kisebbségi töltéshordozók, míg az n típusúban az elektronok a többségi és a lyukak a kisebbségi töltéshordozók.

Nem csak a négy külsõ vegyértékelektronnal rendelkezõ elemek használhatók félvezetõ alapanyagként, hanem ha egyes három és ötvegyértékû, vagy kettõ és hatvegyértékû elemeket egyenlõ arányban helyezünk el a kristályrácsban, az hasonló felépítésû lesz, mint az elõbb a Si esetén láttuk. Ilyenek pl. a Ga-As és a Zn-S alapú félvezetõk. Ha az egyik összetevõ arányát ezekben a kristályokban kismértékben megváltoztatjuk, p ill. n típusú félvezetõt kaphatunk, aszerint, hogy a kisebb vagy a nagyobb elektronszámú elem aránya a nagyobb.

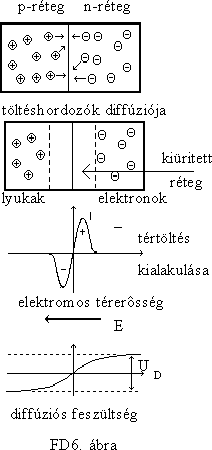
A p-n átmenet

Ha a félvezetõkristály egyik felét donor, a másikat akceptoratomokkal szennyezzük, a kétféle p és n típusú félvezetõ közti határréteget nevezzük p-n átmenetnek. A hõmozgás miatt a határfelületen át elektronok jutnak a p típusú rétegbe és lyukak kerülnek az n típusúba. Ez a diffúziós folyamat nem vezet a két különbözõ töltéshordozó teljes kiegyenlítõdéséhez a kétféle rétegben. A p típusú anyagba behatoló elektronok a határréteg közelében lévõ lyukakkal - míg az n típusú kristályba bejutott lyukak - az ott többségben lévõ elektronokkal rekombinálódnak, kölcsönösen semlegesítik egymást. A határréteg két oldalán lévõ donor és akceptoratomok helyhez kötött ionjai miatt a félvezetõ anyag ezen részei elektromosan nem lesznek semlegesek, töltött zóna alakul ki a határréteg két oldalán, a p típusú rétegben a negatív ionok miatt negatív töltés, az n típusú rétegben a pozitív donoratomok miatt pozitív töltés lesz jelen. Ez a tértöltés olyan irányú elektromos erõteret hoz létre a határrétegben, amely a további diffúziót megakadályozza, az elektronokra az n típusú réteg irányába, a lyukakra a p típusú réteg felé ható taszítóerõ hat. (FD6.ábra) Ennek eredményeképpen a határrétegben gyakorlatilag nem lesznek sem elektronok, sem lyukak. A töltéshordozók hiánya miatt kiürített rétegnek nevezzük a határréteget. A tértöltésnek megfelelõen potenciálkülönbség lesz a két réteg között. Ezt a feszültséglépcsõt nevezzük diffúziós feszültségnek. Ennek értéke Si esetén kb. 0.6 - 0.7 V, Ge-nál kb. 0.2 - 0.3 V, Ga-As esetén 1.5 - 2 V körüli érték. A diffúziós feszültség megakadályozza a töltéshordozó-kiegyenlítõdést a határrétegen át.

A p-n átmenet külsõ feszültség hatására

Kapcsoljunk feszültséget a p-n átmenetre úgy, hogy a feszültségforrás pozitív pólusa az n rétegre, a negatív pólusa pedig a p rétegre kerüljön. Ennek következtében a többségi töltéshordozók ( az elektronok az n rétegben - és a lyukak a p rétegben) a határfelülettõl távolabb húzódnak, mert a zárórétegben lévõ diffúziós potenciált a külsõ tér megnövelte. Ez a hatás a kiürített réteget szélesíti. A határrétegen át csak a kisebbségi töltéshordozók szállítanak áramot, mert rájuk nézve a kialakult térerõsség a határréteg irányába mutat. (FD7.ábra) Ilyenkor a p-n átmenet záróirányú elõfeszítésérõl beszélünk. A kisebbségi töltéshordozók a hõmérsékleti gerjesztés hatására folyamatosan keletkeznek, de (mint nevük is jelzi) számuk több nagyságrenddel kisebb a többségieknél, ezért az általuk szállított áram nagyon kicsi, és nem a feszültség, hanem a töltéshordozók (hõmérséklettõl függõ) száma határozza meg az áram nagyságát, tehát az így elõfeszített p-n átmenet áramgenerátorként mûködik. Az így létrejövõ áramot záróáramnak nevezzük. Ha növeljük a zárófeszültséget, a kiürített rétegben az elektromos térerõsség akkora értéket érhet el, amely kiszakítja az elektronokat a kötésbõl, és így a töltéshordozók száma, és ezzel a záróirányú áram növekedni kezd. A szabad elektronok a nagy térerõsség hatására gyorsulnak, mozgási energiájuk nõ, amelyet a kristály atomjaiba ütközéskor leadnak, és ez az energia újabb elektronokat szakít ki a kötésbõl. Ez egy lavina effektust eredményez, és a záróréteget hirtelen elárasztják az elektronok és a lyukak, az áram ugrásszerûen megnõ. Ha nem korlátozzuk megfelelõen az áramot, a kristály túlmelegszik és tönkremegy. Ezt a jelenséget Zener német fizikusról Zener effektusnak nevezzük.

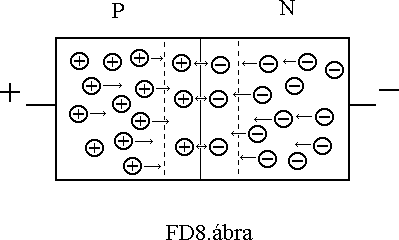
Fordítsuk meg a feszültségforrás pólusait a p-n átmenet sarkain. A záróréteg potenciálja a diffúziós és az ellentétesen kapcsolt külsõ feszültség eredõje lesz. Az eredõ irányát az szabja meg, hogy a külsõ feszültség kisebb-e vagy nagyobb a diffúziós feszültségnél. Amíg a külsõ potenciál értéke a kisebb, a határrétegben nincsenek töltéshordozók, mert az eredõ potenciál ez ellen hat, így az átmeneten nem folyik áram. Ha a külsõ feszültséget addig növeljük, míg túlhaladja a diffúziós potenciált, az eredõ elektromos tér a többségi töltéshordozókat a kiürített zónába vonzza, és a p-n átmeneten keresztül áram folyik. Az n típusú rétegbõl elektronok áramlanak a határrétegbe, míg a p típusúból lyukak, és a határréteg tartományában egymással találkozva rekombinálódnak. (FD8.ábra) A p-n átmenet ilyenkor nyitóirányban van elõfeszítve.

Ha túllépjük a nyitóirányú küszöbfeszültséget, a p-n átmeneten folyó áram nagyon meredeken emelkedik. A zárórétegbe mindkét oldalról nagy számban áramlanak be a lyukak és elektronok, majd ott rekombinálódnak. Ha nem korlátozzuk az áramot, a záróréteg hõmérséklete a megengedett érték fölé nõhet (Si esetén kb. 200 Co, Ge-nál kb. 90 Co) és a félvezetõ tönkremegy.

Félvezetõ diódák

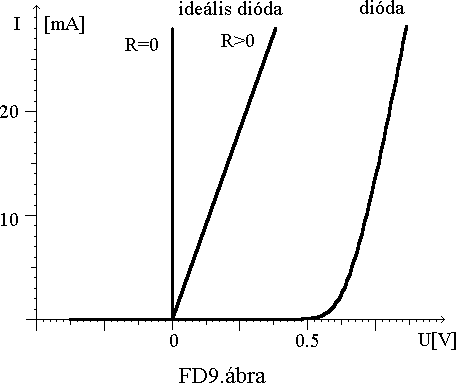
Az egykristály félvezetõ diódákban a p-n átmenet tulajdonságait használjuk ki. A félvezetõ kristályban egy p és egy n típusú réteget alakítanak ki megfelelõ szennyezés hozzáadásával, így a határukon p-n átmenet jön létre. Ez az átmenet úgy mûködik, mint egy áramszelep, egyik irányban az áramot átengedi, másikban nem folyik áram. A valóságos dióda tulajdonságai természetesen kissé különböznek az ideálistól. (FD9.ábra)

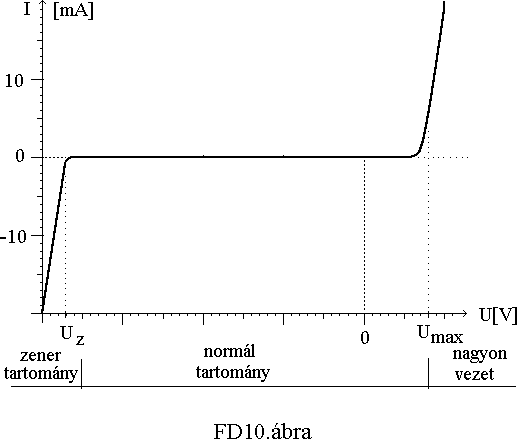
A dióda jellemzõit a FD10.ábrán található feszültség-áram jelleggörbén tanulmányozhatjuk. Kis nyitóirányú feszültség esetén, amíg a diffúziós potenciálgát nagyobb, a diódán gyakorlatilag nem folyik áram (csak visszáram nagyságrendû). Ha a külsõ feszültség eléri a diffúziós potenciál értékét, a küszöbfeszültséget (ami Si esetén kb. 0.6V, Ge-nál pedig kb. 0.2V) az áram megindul és meredeken emelkedni kezd. A jelleggörbe exponenciális jellege Umax értéknél lineárissá válik. Ezt mutatjuk be a nyitókarakterisztika egy kinagyított részletén. (11. ábra) A dióda csak a küszöbfeszültség felett kis ellenállású és ennek értéke a munkaponttól függ.

Megkülönböztethetünk egyenáramú és differenciális ellenállást. Az egyenáramú ellenállás értéke a diódán esõ feszültség és az átfolyó áram hányadosa: Re=UM/IM, (UM és IM a munkaponti feszültség és áramérték). A differenciális ellenállás a görbe meredekségét adja meg az adott munkapontban, tehát az oda húzható érintõ iránytangensét, azaz differenciálhányadosát (pontosabban ennek reciprokát, ld. I. fejezet). Ezt közelítõleg a feszültség kis megváltozásának és a hozzátartozó áramváltozásnak a hányadosaként számíthatjuk ki: rd= U/ I.

Ha a diódára a p-n átmenet záróirányának megfelelõ feszültséget kapcsolunk, az ú.n. záróáram folyik, tehát a dióda nem zár tökéletesen. Ezt azonban az alkalmazások során általában elhanyagolhatónak tekinthetjük, szokásos értéke Si esetében néhány nanoamper (nA), Ge esetén elérheti a mikroamperes ( A) értéket is. Mivel ezt az áramot a kisebbségi töltéshordozók okozzák, értéke erõsen hõmérsékletfüggõ.

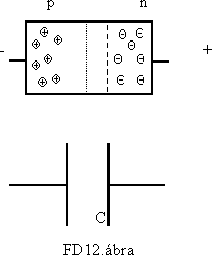
A záróirányban elõfeszített dióda leginkább egy kondenzátorra hasonlít. A két fegyverzet a p és az n réteg, a köztük lévõ kiürített záróréteg szigetelõként viselkedik. Mivel a kiürített réteg szélessége a rákapcsolt záróirányú feszültséggel nõ, a dióda-kondenzátor kapacitása csökken a zárófeszültség növekedésével, így olyan kondenzátort kaptunk, amelynek a kapacitását a rákapcsolt feszültséggel szabályozhatjuk. (FD12.ábra)

Ha a záróirányú feszültség eléri a zener feszültséget, bekövetkezik a zener letörés. A dióda ezen a szakaszon egy Rz nagyságú ellenállással helyettesíthetõ.

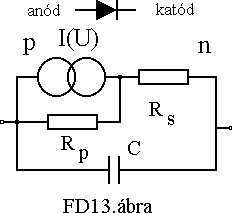
Az elõbbiek alapján megadjuk a diódának a TINA áramkörszimulációs program által használt helyettesítõ képet, a dióda rajzjelét és modelljét. (FD13.ábra) A dióda rajzjelének nyíliránya a konvencionális pozitív áramirányt mutatja (technikai áramiránynak is nevezik). Az elektródáknak anód ill. katód a szokásos elnevezésük.

A dióda árama (I) és a p-n átmeneten esõ feszültség (Upn) között fennálló matematikai összefüggések bonyolultak, nemlineárisak és szakaszosan különbözõk. Az alábbiakban közölt függvények maximálisan egyszerûsítettek, de fizikailag még korrekt eredményt adnak.

A diódát leíró egyenletek a különbözõ mûködési szakaszokban:

Zener szakasz:

"Normál" tartomány:

Nagyon vezet:

Telítési áram hõfokfüggése: Is = Iso (T/To)3 exp[(1/To-1/T)Eq/k]

Kapacitások nagysága, feszültségfüggése:

Cd = t   / rd rd = dUpn/ dI ha Upn >  0 egyébként Cd = 0

Csc = CJ0 (1- Upn / UJ )-M ha Upn   < UJ / 2

Csc = 2M CJ0 [(2M Upn / UJ) + 1 - M] ha Upn   > UJ / 2

C = Csc + Cd

A paraméterek tipikus értékei:

Iso telítési áram 300 K-en 5 fA

Uz Zener feszültség 35 V

Rz Zener ellenállás 10 ohm

Rp párhuzamos ellenállás 100 kohm (végtelen)

Rs soros ellenállás 5 ohm (nulla)

  t diffúziós idõállandó 100 ns

CJ0 tértõltési kapacitás 20 pF

UJ diffúziós potenciál 750 mV

M kitevõ kapacitás számoláshoz 0.33

E tiltott sáv Si-ban 1.11 V

UT termikus feszültség 25 mV

To szobahõmérséklet 300 K

Umax maximális feszültség 1.04 V

Upn a dióda feszültsége

q elemi töltés

Mivel a dióda áram-feszültség függvényének a differenciálhányadosa minden pontban a vezetõképességet adja, a megadott egyenletek alapján a differenciális (dinamikus) ellenállása rd   UT / I .