Fourier sorok, elvi és gyakorlati jelentôségük.

Ebben a fejezetben az elektromos jelek két, egymáshoz rendelt, de szemléletükben - matematikailag és fizikailag - különbözô értelmezésérôl lesz szó. Természetesen megállapításaink nem korlátozódnak elektromos jelekre.

Mindenekelôtt meg kell ismerkednünk a Fourier nevéhez fûzôdô jelfelbontás lényegével és annak technikai következményeivel.

Fourier lényegében arra jött rá, hogy a periodikus jelek elôállíthatók egy alapfrekvenciájú szinuszos jelnek, valamint ennek felharmonikusainak összegeként.

Felharmonikusnak az olyan szinuszos jelet nevezzük, amelynek frekvenciája az alapfrekvencia egészszám-szorosa. - Próbáljuk ezt most belátni, tudva azt, hogy az egész mögött egzakt, bonyolultnak nevezhetô matematikai formalizmus is létezik.

Jelenlegi tanulmányaink szempontjából a lineáris hálózatokon az elektromos jelenségeknek három alapvetô típusa létezik:

a. A rendszert már régóta gerjeszti egy szinuszos generátor. Ekkor a kimenetén is szinuszos jel jelenik meg. Azt lehet vizsgálni, hogy különbözô frekvenciákon a bemenet hányadrésze jut a kimenetre, illetve mekkora a bemeneti és kimeneti szinuszos jelek közötti fázisszög.

Ezt szinuszos gerjesztésû, állandósult állapotú rendszer vizsgálatának hívjuk. A gyakorlati elektrotechnikában igen nagy a jelentôsége. Számításához egyszerû fogalmak (pl. impedancia), kidolgozott matematikai eljárások állnak rendelkezésre. - Az ilyen vizsgálatok eredményének összefoglalása jelenik meg az ún. frekvencia-karakterisztikán, vagy ennek egy formájában, a Bode diagramon.

b. A rendszer bemenetére valamilyen határozott, egyszer megjelenô jelalakot adunk. A vizsgálatok szempontjából ezek leggyakrabban ugrás (lépcsô) függvények, vagy rendkívül rövid impulzusok. Természetesen ide tartoznak azok a folyamatok is, amikor egy szinuszos generátort kapcsolunk "hirtelen" a vizsgálni kívánt rendszerre. - Ilyenkor a kimenet idôbeni változásának lefutását, "történéseit" keressük, - ezt leggyakrabban "bekapcsolási jelenségek vizsgálata" névvel illetik

c. A bemenôjel periodikus, vagyis 2T idôközönként ismétlôdik. A periódusidôn belül nem teszünk - fizikai szempontból lényeges - kikötést a jel alakjára. A jelben diszkontinuitások is elôfordulhatnak, vagyis impulzusszerû, ugrásokkal tarkított jelszakaszok is megengedettek.

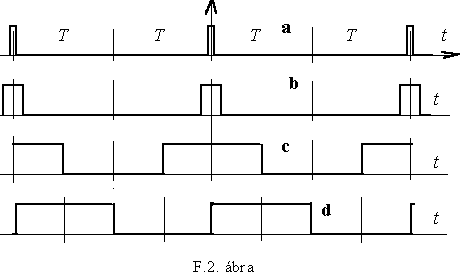
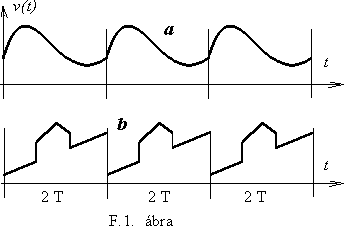
Az F.1. ábra "a" részén egy valóságos periodikus jelet mutatunk, ami például valami folyamat ismételt mérésébôl származhat. A "b" jelben több szakadás, ugrás is található. Az F.2 ábra ugyanakkora - 2T - periódus idejû, de különbözô szélességû impulzusokat mutat (a - c). A "c" az ún. szimmetrikus négyszögjel, ahol a jel idôtartama éppen T. "d" ugyanaz a jel, idôben azonban késleltetve.

Fourier felfedezése azt jelenti, hogy minden, 2T periódusidejû ismétlôdô v(t) jel elôállítható egy állandó érték (ao/2), valamint szinuszos/koszinuszos jelek összegeként, vagyis:

ahol k pozitív egészszám (1, 2, 3, stb.) az ak és bk együtthatók pedig az ún. Fourier komponensek számértékei.

Vizsgáljuk meg, hogy mit is jelent ez az összefüggés! Ha k = 1 , akkor egy teljes szinusz/koszinusz hullám ismétlôdési hossza éppen 2T. Ha k = 5, akkor 2T idôtartam alatt éppen öt teljes hullám zajlik le. A k = 1 - hez tartozó szinuszos/koszinuszos jelet alapfrekvenciának, alapharmonikusnak nevezzük, a többit pedig a megfelelô számú felharmonikusnak. A v(t) idôfüggvényt tehát az alapfrekvencia és a felharmonikusok szerencsésen súlyozott értékeinek - végtelen - összegébôl állíthatjuk elô. (Emlékezzünk csak: azonos frekvenciájú szinuszos és koszinuszos jelek összege szintén szinuszos jellegû lesz, persze eltérô amplitúdóval, és eltérô fázissal. Az ak és bk együtthatókkal rendelkezô azonos frekvenciájú szinuszos és koszinuszos jelek egyetlen eltolt fázisú szinuszos jellé kombinálhatók!)

Az ak és bk együtthatók a v(t) függvény ismeretében az alábbi összefüggésekkel kaphatók meg:

(A képletek azonnal sugallják: a szinuszos jelek páratlan volta miatt az anti-szimmetrikus, páratlan függvények csak szinuszos komponensekbôl is összerakhatók. - Természetesen ennek megfelelôje szintén igaz: a páros függvények csak koszinuszos összetevôkbôl állnak.)

Ezen összefüggésekkel és értékelésükkel részletesen foglalkozik majd a Jelfeldolgozás c. tantárgy. Itt a pontos leírás helyett csak átfogó, kvalitatív képet kívánunk kialakítani a Fourier módszer jelentôségérôl.

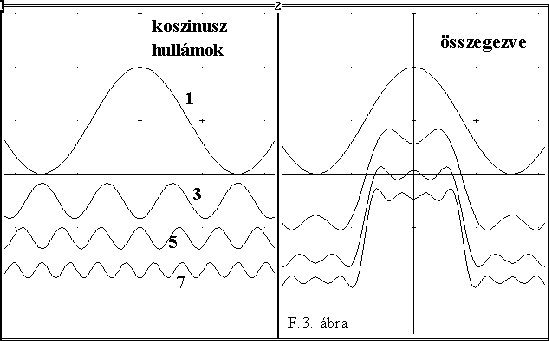
A viszonyok megértéséhez lássunk egy egyszerû példát. Tételezzük fel, hogy egy T idôtartamú, 2T idônként ismétlôdô ún. szimmetrikus négyszögjel (F.2.c. ábra) Fourier komponenseit a fenti képletek alapján meghatároztuk. Az ebben az esetben nehéznek nem nevezhetô matematikai kiértékelésbôl az alábbi értékeket kaptuk:

a bk értékei pedig zérusok. Csak koszinuszos komponensek léteznek, mivel az eredeti függvény páros volt. Meglepô, hogy a páros rendszámú komponensek amplitúdója zérus, - szinuszos összetevôk ebben a jelben pedig egyáltalán nincsenek. Vagyis az eredeti függvény közelítése:

Az F.3. ábra baloldala az a1 -7 együtthatókkal felrajzolt, megfelelô frekvenciájú koszinuszos jeleket mutatja. - Szinte hihetetlen, de ha ezeket összeadjuk, eredményül a szimmetrikus négyszögjelet elfogadható közelítésben kapjuk vissza. Az F.3. ábra jobboldalán - felülrôl lefelé - egyre több komponenst adunk össze, - a legalsó görbe az a1 -7 komponensek összegét mutatja. A közelítés annál jobb, minél több komponenst összegezünk

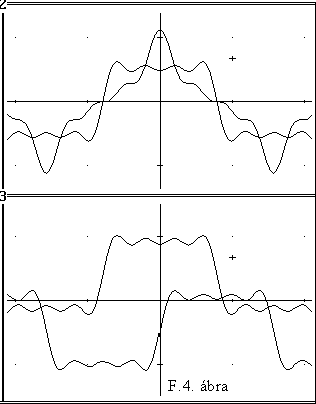
Csináljuk egy ellenpéldát annak szemléletessé tételére, hogy a megadott együtthatók ténylegesen "jók": és változtassuk a negatív elôjeleket is pozitívra. Az eredmény valami egészen más lett (F.4. ábra felsô részén látjuk a torzítatlan és a beavatkozásunk miatt eltor-zult függvényt), az eredeti jelet még csak sejteni sem lehet. Ennek oka az, az elôjelek megváltoztatásával módosítottuk a komponensek fázisviszonyait is. A fázis ugyanannyira fontos, mint az amplitúdó !

Ha a szimmetrikus négyszögjelet az X tengely mentén T/2 értékkel eltoljuk, akkor az elôbb még páros függvénybôl páratlant csináltunk. Most csak szinuszos összetevôk lesznek, azok számszerû értékei azonban meg fognak egyezni az elôzôekben már jónak bizonyult értékekkel:

Az azonos együtthatójú koszinuszos és szinuszos jelek összegét az F.4. ábra alsó részén láthatjuk

Az F.5. ábrán a

komponensek összegét ábrázoltuk. (Itt most vannak páros rendszámú felharmonikusok is !) Bár a komponensek számértékei némileg emlékeztetnek az elôzô példák értékeire, ezek eredôje most lineárisan emelkedô, ún. fûrészfog jelalak, mely egyáltalán nem emlékeztet a szimmetrikus négyszögjelre.

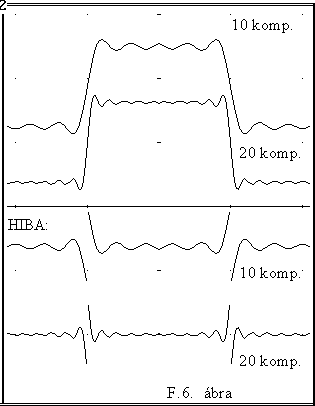
A definíciós képlet szerint azonban az eredeti négyszögjelhez végtelenül sok komponenst kellene összegezni, ami gyakorlatilag alig kivihetô. - Az F.6. ábra a tizedik és huszadik felharmonikusig történô összegzéssel keletkezô jeleket tünteti fel, illetve az eredeti négyszögjeltôl való eltérést, ugyanolyan vízszintes és függôleges skálával. Az ábra részleteinek figyelmes szemlélésével a Fourier közelítés sok fontos jellemzôje is felfedezhetô.

A Fourier sorok (tágabb értelemben: transzformáció) igen jelentôs érdeme az, hogy rámutat arra, hogy

1. minél több komponenst összegezünk, annál pontosabban visszakapjuk az eredeti jelet. (az elhanyagolt komponensek - végtelen sok! - adják az eltérést, a hibát).

2. az esetek többségében elegendô a végtelen sok komponensbôl csupán annyit venni figyelembe, amennyibôl gyakorlati szempontból az eredeti jelet visszakapjuk. Vagyis elégséges lehet a periodikus jel (alap)frekvenciájának 5 - 10 - 20 - szorosának megfelelô frekvenciakomponenseket számításba venni. - A Fourier módszer tehát fontos eszközt jelent a valóságban szükségképpen mindig véges sávszélességû rendszerek jeltorzítási hatásainak vizsgálatában, tervezésében.

A Fourier együtthatók szerepe, jelentôsége másként is értelmezhetô. Gondoljuk arra, hogy szinuszos jelet úgy kaphatunk, ha pl. egy biciklikereket állandó fordulatszámmal körbeforgatunk és a kerület egy meghatározott pontját - a kerék síkjával párhuzamosan, erre merôleges falra vetítjük. Ha a fal síkjában egy papírlapot mozgatunk egyenletes sebességgel, ezen az árnyék szinuszos jelet rajzol.

Képzeljük a fenti példa adatai alapján azt, hogy a kerék elôbb kitüntetett pontjában egy újabb kereket helyezünk el, amelyik háromszor akkora sebességgel forog, mint az elôzô és sugara ennek harmadrésze. Ennek kerületéhez csatlakozik egy újabb, most már ötszörös szögsebességgel forgó kerék, persze ez is megfelelô sugárral. - Ezt ábrázolják az F.7. ábra vektorai, amelyek forgás közben egy különösen mozgó (rángatódzó?) rendszert alkothatnak.

A Fourier komponensekre bontás azt állítja, hogy e furcsa rendszer végpontjának árnyéka képes két - állandónak tekinthetô - érték között szinte ugrásszerûen változni.

Amit a továbbiak érdekében tudatosítanunk kell: az idôben lezajló (periodikus) folyamatok matematikai szimbolizmussal leírt változatai, valamint ezek Fourier komponensekbôl összerakott közelítései egyaránt alkalmasak a villamos jelek reprezentálására.

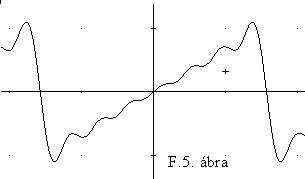
Ha "az idôtartományban gondolkodunk", akkor az elôbbi a természetes, - ha a jelek átvitelének frekvenciakarakterisztikája adott, akkor az utóbbi az elônyösebb.

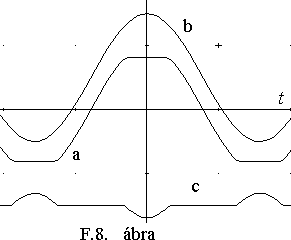
Nézzünk erre egy példát. Gyakran elôfordul, hogy egy szinuszos jel nonlineáris hálózaton halad keresztül, pl. tranzisztoros erôsítôfokozaton. A tápfeszültség korlátos volta miatt a szinuszos jelek eltorzulnak, rendszerint a tetejük "megskalpolódik". Ezt látjuk az F.8. a. ábrán. Ez a megvágott jel azonban elôállítható az eredeti szinuszos jel (b), valamint a (c) jel összegébôl. A (b) jel csak egyetlen frekvenciakomponenst tartalmaz, a (c) azonban - lévén periodikus és nem szinuszos - végtelen sokat. Igy eljutottunk ahhoz a nagyon fontos megállapításhoz, hogy az amplitúdótorzítás felharmonikusokat kelt. Ezt érzékelik a hi-fi technika megszállottai, aminek az az eredménye, hogy elképesztôen nagy teljesítmények kezelésére szolgáló erôsítôket készítenek, amelyeket szinte egyáltalán nem használnak ki.

Végezetül ismételten hangsúlyozzuk, hogy a Fourier módszer a jelek világának szinuszos-koszinuszos komponensekre bontásának, összerakásának eszköze. Ilyenkor természetesen nem csak egyetlen dimenzióra korlátozódunk. Egy hegyes-völgyes tájat, vagy esetleg egy képet is felbonthatunk egymásra merôleges hullámú komponensekre. - Nem kell meglepôdnünk azon, hogy a jelek másfajta függvényekre is felbonthatók, (ennek a megoldandó feladathoz kell simulnia) - a matematikusok nem tétlenkedtek. A szinuszos jelek azonban kiemelkedô fontosságúak, mivel ezek - mint már láttuk - lineáris elemekbôl álló hálózatokon alaktorzulás nélkül haladnak át. Azt is látni fogjuk majd, hogy ezek a jelkomponensek számos, egyébként csak nehézkesen elvégezhetô számítást képesek radikálisan egyszerûsíteni.

E rész befejezéséül "költôi hasonlattal" élünk. Escher egy szép rajzának részletét mutatjuk az F.10 ábrán. Ez a szellemes képi konstrukció egy kört rak össze különbözô méretû (szinuszos?) ördögökbôl és (koszinuszos?) angyalokból. Escher rajza a "felharmonikusok" jelentôségét is sejteti.

Feladatok:

Az alábbi feladatok megoldásához részben gondolkodásra, részben pedig számítógépre is szükség lesz.

1. Írja fel a 3 SIN (t + p /8) jelet fázisszög nélküli szinusz és koszinuszhullám eredôjeként.

2. A megadott függvények a -1 > t £ 1 tartományban értelmezettek, T = 2 szerint periodikusak. Rajzolja fel (kvalitatíve) ezeket függvényeket. Melyek ezek közül azok, amelyek Fourier komponensei között csak koszinuszos, illetve csak szinuszos komponensek fordulnak elô?

a. y = t2 b. y = ABS(t) + 3

c. y = SIN(2 p t) d. y= SIN(2 p t + p /6)

e. y= COS(t2) f. y = t5

g. y = t + ABS(t) h. y = 1/t

3. Bontsa fel az alábbi függvényt páros és páratlan összetevôkre:

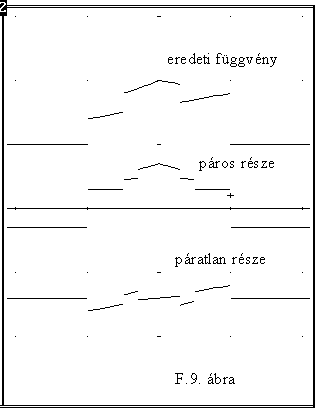
4. Kísérelje meg felbontani az F.1. "b" ábra szerinti függvény 2T hosszúságú szakaszát egy páros és egy páratlan függvény összegére. (A megoldás az F.9. ábrán látható.)

5. Mutassa meg, hogy a 2 T = [-1, +1] között definiált periodikus SIN(p t) függvénynek nincsenek felharmonikusai, - ha azonban jel frekvenciáját megváltoztatjuk SIN([p +d ]t) -re, ahol d nem p egészszámú többszöröse, megjelennek a felharmonikusok.

6. Rajzolja fel az egy-, illetve kétoldalasan egyenirányított hálózati feszültség ábráját. Határozza meg, hogy az egyenirányított jeleknek mekkora a hálózati frekvenciájú komponense.

7. Az alábbi táblázatban megadjuk három (A,B,C) jel Fourier komponenseit. Ábrázolja ezeket lehetôleg úgy, hogy az eredô jelek amplitúdói körülbelül azonosak legyenek. Mi a hasonlóság, vagy különbség a három jel között?