Bekapcsolási jelenségek

Az elektronikus áramkörök igen jelentôs csoportjainak - impulzustechnika, digitális technika - viselkedése csak a ténylegesen létrejövô feszültség, vagy áram függvények segítségével tanulmányozható. Ez pedig - a legtöbb esetben - az áramkörben található kondenzátorok jelalakjainak vizsgálatát jelenti.

(Természetesen azok az alkalmazások is fontosak, ahol induktivitások/tekercsek fordulnak elô. Érdekes módon azonban sok helyütt igyekeznek ezeket az elemeket elkerülni. A velük kapcsolatos óvatosságra leginkább az int, hogy a lineáris alkatelemek közül legkevésbé az tekercsek integrálhatók. Induktivitások használata esetén nem kicsiny annak a veszélye, hogy ezek elkerülhetetlen kölcsönös csatolásai az áramkört megbízhatatlanná, nehezen számolhatóvá, esetleg gerjedékennyé teszik. - Az induktivitást tartalmazó körök jelalakjainak kiszámítása ugyanolyan módszerekkel történhet, mint a kondenzátort tartalmazóké.)

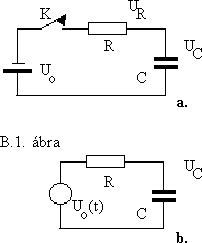
A B.1 ábra a. részén a lehetô legegyszerûbb - egyetlen kondenzátort és ellenállást tartalmazó - kapcsolást látjuk. Tegyük fel, hogy a kondenzátor feszültsége vizsgálatunk kezdetén zérus. A kapcsoló zárásával áram indul, amelyik a kondenzátort tölteni kezdi. - Hosszú(?) idô múlva a kondenzátor feszültsége a telep feszültségével egyezik meg, - áram tovább nem folyik.

Ha a kapcsolót most megszakítjuk, akkor a kondenzátoron a feszültség megmarad. Persze tudjuk, hogy valóságban ez nem lehetséges, mert a tényleges kondenzátorokhoz mindig kapcsolódik párhuzamos veszteségi ellenállás, amelyiken hosszabb rövidebb idô alatt kisülnek. Ezt az idôt azonban csak becsülni tudjuk.

A B.1. ábra b. része ezt az ún. bekapcsolási folyamatot egy különleges feszültséggenerátor beiktatásával teszi vizsgálhatóvá. A feszültséggenerátor belsô ellenállása mindig zérus, feszültsége azonban az idôben változik: hirtelen felugrik U0 értékre, majd T idô múlva ismét nulla lesz. Vegyük észre, hogy az elôbbi töltôdési folyamatot így is vizsgálhatjuk, - a bemeneti feszültség megszûnte után azonban a kondenzátor a (pontosan definiált) R ellenálláson keresztül sül ki.

Az áramkörre vonatkozó alapvetô Kirchhoff egyenlet:

Kicsit átalakítva és kihasználva, hogy a bemeneti feszültség állandó

Ez az egyszerû differenciálegyenlet a bekapcsolási feszültségugrás esetére könnyen megoldható és a kezdeti feltételek ( UC = 0 ) figyelembe vételével a következô lesz:

az ellenálláson és a kondenzátoron létrejövô idôfüggvények pedig:

Ezeket az összefüggéseket nagyon alaposan meg kell érteni és a gondolatmenetet "ösztönösen" kell alkalmazni hasonló feladatok megoldásánál.

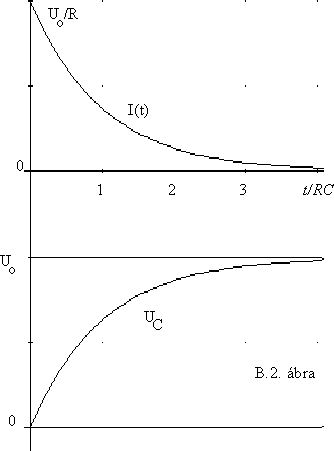
A bemeneti feszültség megjelenésének idôpillanatá-ban - a kondenzátor feszültsége zérus - a feszültség teljes egészében az ellenállásra kerül. Az áram kezdeti értéke tehát U0 /R lesz. - A kon-denzátor feszültsége a felgyü-lemlô töltések hatására növek-szik, - ugyanekkora értékkel csökken az ellenálláson mér-hetô feszültség. - Elegendôen hosszú idô múlva a konden-zátoron a teljes bemeneti feszültségugrás megjelenik, az ellenálláson pedig nem talá-lunk feszültséget. (Mechani-kából vett analógiaként érde-mes az úszóval szabályozott vízöblítô tartályok feltöltôdési folyamatára gondolni...)

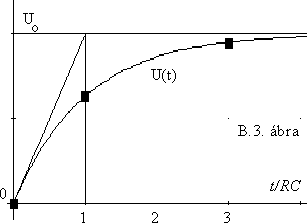
A kialakuló hullámalakokat a B.2. ábrán láthatjuk: RC idôállandójú exponenciális idôfüggvény határozza meg ôket. Mivel ilyen jellegû függvények rajzolására gyakran lesz szükségünk, egyszerû módszert ajánlunk ehhez. Példaként felrajzoljuk a kondenzátor feszültségváltozását (B.3. ábra):

- berajzoljuk a görbe kezdôpontját (ez most zérus)

- berajzoljuk azt a vízszintest, ahova görbe tartani fog.

- a t/RC = 1 értéknél függôlegest húzunk, majd megrajzoljuk a négyszög átlóját (ez illeszkedik az exponenciális kezdeti meredekségéhez)

- "megsaccoljuk" a függôleges kétharmadának helyét ( 1 - e-1 @ 2/3 ), - ehhez szemünk és a hozzá tartozó "komputer" különösen alkalmas,

- a t/RC = 3 távolságnál megtippeljük a 0.95 értéket

- a t/RC = 5 értéknél elérjük a végsô értéket (ez otromba közelítés, mert matema- tikailag még soha egyetlen exponenciális idôfüggvény sem fejezôdött be....)

A késôbbiekben gyakran fogjuk követni azt az utat, mely a bonyolultabb eseteket is a fenti alapproblémára vezeti vissza. - Ennek során igyekszünk csak olyan áramkörökkel foglalkozni, amelyekben több ellenállás, de csak egyetlen kondenzátor van (vagy fordítva, de ez eléggé ritka). Bonyolultabb eseteket vagy nem vizsgálunk, vagy kegyes csalással leegyszerûsítjük. - Vegyük észre: a sok ellenállásból és egyetlen kondenzátorból álló köröknek csak egyetlen idôállandójuk van a mûködés összes fázisában !

Egyszerû eljárásunk a feladat grafikus megoldásához vezet:

elsô lépésként a bekapcsolási jelenséget elôidézô kapcsoló, vagy vezérelt jelforrás mûködése elôtti állapotban megállapítjuk a kondenzátor feszültségét;

meghatározzuk a kondenzátoron a mûködés után igen hosszú idô múlva kialakuló feszültség értékét;

a kondenzátor felôl "benézve" az áramkörbe meghatározzuk az innen látható ellenállás értékét és ebbôl az idôállandó nagyságát;

a fenti exponenciális görbe rajzolási metódusát alkalmazzuk. (L. 5. feladat.)

Felfutási idô, legrövidebb jel

A B.4. ábra azt mutatja, hogy milyen lesz a kondenzátoron kialakuló jelalak akkor, ha a B.1.b. ábra szerinti kapcsolást tekintjük érvényesnek.

Jól látszik, hogy a kondenzátor - amelyen feszültség-ugrás sohasem jöhet létre ! - kimeneti jelének felfutó szakasza lineáris növekedéssel kezdôdik, ami késôbb lelassul. Hasonló a helyzet a bemeneti impulzus lefutó élénél.

Míg a bemeneti jel felfutó szakasza végtelen nagy meredekségû volt, a kimenet - legalább kezdetben - csak lineárisan emelkedik. Ennek a mérsékelt emelkedési jelenségnek a számszerû jellemzésére bevezették a felfutási idô fogalmát. - A felfutási idô a jel emelkedô szakaszán a végleges érték 0.1 és 0.9 része közötti szakasz megtételéhez szükséges idôtartam. (Természetesen ez a definíció is önkényesnek tûnik. Mentségére szolgál, hogy könnyen és egyértelmûen mérhetô.) Természetesen a lefutási idôre értelemszerûn azonos definíció létezik.

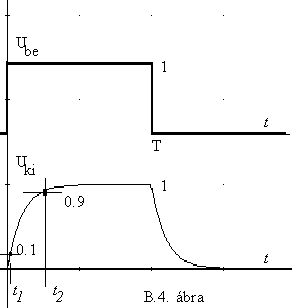
A felfutási idô meghatározásához - az ábra szerint - az alábbi összefüggéseket lehet felírni:

B.6. és B.7. -bôl meghatározhatjuk a felfutási idôt és eredményként azt kapjuk, hogy:

Ez a képlet önmagában is értékes, hiszen ebbôl meghatározhatjuk a "legrövidebb" kimenô impulzus szélességét. Kicsit nagyvonalúan gondolkodva ugyanis azt mondjuk, hogy ez a felfutási és lefutási idôk összege, vagyis a felfutási idô kétszerese.

Van azonban egy, a fenti megállapításnál nagyobb horderejû következmény. A B.1.b. kapcsolási elrendezés teljesen azonos a T.6. ábrán látható aluláteresztô szûrôével. Itt megállapítottuk, hogy a felsô határfrekvencia:

Ha RC értékét ebbôl kifejezzük és a B.8. - ba helyettesítjük, akkor ahhoz az igen fontos összefüggéshez jutunk, hogy:

Már láttuk azt, hogy valóságos elektromos rendszereknek óhatatlanul van felsô frekvenciahatáruk. Most azt látjuk, hogy az ilyen rendszerekhez a legrövidebb kimenô impulzus fogalma is hozzátartozik. Érdekes módon a kettô szorzata kb. egységnyi. (Legalább nagyságrendileg. A fenti gondolatmenet pontatlanságai ellenére is gyakorlati szempontból jól használható eredményre vezetett. Késôbb a Jelfeldolgozás tárgyban, - kissé általánosabb érvénnyel - ugyanide fogunk elérkezni.)

A fenti összefüggés jelentôségének hangsúlyozására el kell gondolkodnunk azon, hogy egyes jelforrások milyen frekvenciasávú jelet is keltenek.

Hangfrekvenciás - beszéd, zene - jelek legmagasabb frekvenciájú komponensei elérhetik a 20 kHz értéket (ezt persze csak a "vájtfülûek" hallják, de csak akkor, ha eléggé fiatalok). A hangszerek, valamint az emberi gége 20 Hz alatti jelek keltésére alkalmatlan.

Érdekes eset a telefon. Itt mûszaki/gazdasági okok miatt erôteljesen csökkentik a sávszélességet: kb. 300 - 3000 Hz. tartományra. Az eredmény ismert: a hangminôség rossz lesz, érthetôségi problémák jelennek meg.

A televízió képének legnagyobb frekvenciájú összetevôjét is megbecsülhetjük. A hazai televíziós szabvány szerint a képek 625 sorból állnak. A kellemesen látható kép érdekében a képek vízszintes irányban is legalább ilyen (esetleg jobb) felbontásúak. - A képernyôt gondolatban egy 625 x 625 "pöttybôl" - ezt ebben a szakmában pixelnek hívják - álló négyzethálóval lehetne lefedni. Ennek a négyzethálónak információmennyiség szempontjából maximális kitöltését az jelenti, ha ilyen méretû fekete-fehér elemekbôl álló sakktáblát tételezünk fel. - Egy fekete-fehér pontpár durva megjelenítéséhez/leírásához egyetlen szinuszhullám szükséges.

Mivel a televízió másodpercenként 25 képet sugároz, a képtartalom legmagasabb frekvenciájú komponensei egyszerûen meghatározhatók ( 625 x 625 x 25 / 2 ), és lényegében 4.8 Mhz értéket adnak eredményül. (A számítógépek igen nagy felbontású monitorjainál ez az érték sokkal nagyobbra adódik!).

Mindezekbôl természetesen ki tudjuk számolni, hogy a hangfrekvenciás, illetve televíziós csatornák esetén mekkora a kijövô legkeskenyebb impulzus szélessége.

Befejezô példaként azt becsüljük meg , hogy egy (közismertnek tekinthetô) EKG - vagyis orvosi elektrokardiogram - mechanikus, ún. mozgótollas íróval való felvétele milyen sávszélességû írószerkezetet igényel. - Szívdobbanásaink nagyjából másodpercenként következnek be. Tegyük fel, hogy az orvosok a diagnózisaikhoz ennek az idônek a századrészét is értékelni képesek. - Ebbôl adódik, hogy a rendszer sávszélességének 100 Hz-nek kell lennie, vagyis az írószerkezet 10 - 20 ms. idôtartamú jelek rögzítésére még képes.

Feladatok:

1. A. B.2. összefüggésbe helyettesítse be az áram idôbeli lefolyását leíró egyenletet és igazolja, hogy ez tényleg a differenciálegyenlet (egy) megoldása.

2. Milyen lesz a kondenzátoron kialakuló jelalak akkor, ha a B.1.b. ábra szerinti kapcsolásban RC = T, illetve 5 RC = T ? (T a generátor impulzusának idôtartama.)

3. Milyen idôtartamú a telefonon továbbítható legrövidebb impulzus?

4. Az IBM PC-hez köthetô monitorok közül az ún. VGA manapság a legnépszerûbb. Mekkora a minimális sávszélesség, amin a monitor videojelét továbbítani lehet? (A számoláshoz szükséges adatok az Elektronika jegyzetnek a monitorokról szóló fejezetében megtalálhatók.)

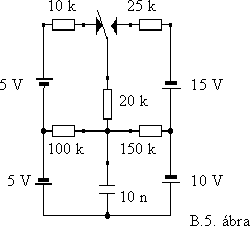
5. A B.5. ábrán látható áramkörben a kapcsoló hirtelen átvált másik állapotába és ott marad. Rajzolja fel a kondenzátoron kialakuló jelalakot.

6. Mekkora lesz a T.14.a. ábra szerinti áramkör kimeneti jelének felfutási ideje, ha a bemenetre áramugrás érkezik?

7. Mekkora lesz a T.12. a. és T.12. d. ábra szerinti kapcsolási elrendezéseken átvihetô legrövidebb impulzus?

8. A B.1.b. ábra szerinti elrendezésben a feszültséggenerátor T periódusidejû pozitív polaritású négyszöghullámot kelt. Az RC áramkör idôállandója T/2. - Rajzolja fel a kimenô jelalakot 3 T idôtartamra.