![]() Im.
1
Im.
1
Váltófeszültség, impedanciák
Lineáris elektromos alkatelemek.
Az elektromos (elektronikus) hálózatok felépítésének három egzaktul lineáris eleme van: az ellenállás, az induktivitás és a kapacitás. Ezek mindenütt jelen vannak, - egyik-másikuk esetleg csak nyomokban, elosztottan, nem mindegyik meghatározó módon. - Természetesen a nonlineáris elemeknek is vannak lineárisnak tekinthetô mûködési szakaszai, pl. félvezetôknek. - (A "lineáris" azt jelenti, hogy n-szer akkora bemeneti hatásra n-szer akkora kimeneti hatás jelenik meg a kérdéses elemen.)
Im. 1.
Az alkatelemeknek a Maxwell egyenleteken alapuló definiáló összefüggései az alábbiak:
![]() Im.
1
Im.
1
Ezek az összefüggések, - amelyek az elektrotechnika legfontosabb szabályait rögzítik tömören, azt mondják el, hogyha bemenô változóként az áramot (ez az "ok"), kimenetként a létrejövô feszültséget (ez az "okozat") tekintjük, akkor
- az ellenálláson kialakuló feszültség idôfüggvénye az áram idôfüggvényével - skálafaktortól eltekintve - azonos,
- az induktivitáson megjelenô feszültség az áram idôbeli differenciálhányadosával arányos,
- a kondenzátor a rajta átfolyó áramot pedig "összegyûjti", vagyis integrálja.
(A továbbiak megértéséhez biztos tudással kell rendelkezni egyszerû függvények differenciálásának és integrálásának szabályairól.)

Nagyon fontos tudatosítani, hogy
- az induktivitáson átfolyó áramban bekövetkezô ugrás elvileg végtelenül nagy feszültséget eredményez, ami esetleg az induktivitást tönkre is teheti;
- a kondenzátoron feszültségugrás csak akkor jelenhet meg, ha extrémen rövid ideig igen nagy (végtelen) áram folyik, - ez gyakorlatilag nem lehetséges;
- a kondenzátor kezdeti töltését zérusnak tekintettük, - ha nem ez igaz, akkor ezt a tényt is figyelembe kell venni.
A fentiek illusztrálására nézzük az Im. 1 ábrát, melyet érdemes figyelmesen és hosszan szemlélni, ellenôrizni, értelmezni. - Itt különbözô, korlátozott ideig tartó áramalakokat tüntettünk fel, hogy az egyes elemeken megjelenô feszültségváltozásokat ábrázolhassuk. - (Természeten az elemek közül kihagytuk az ellenállást, mivel ebben az esetben az áram lefutása és a keltett feszültség lefutása lényegében azonos függvényalakot eredményez.) Az áramalakok: fûrészjel, impulzus, "magányos" szinuszhullám, - elég gyakran elôfordulnak a gyakorlatban. - Az eredmények áttekinthetôek, érdekesek. Talán külön ki kell emelnünk, hogy a szinuszos áramjel hatására a tekercsen kialakuló feszültségalak hirtelen ugrással kezdôdik, - a fûrészjel hatására a kondenzátoron megjelenô jelalak pedig parabola szakaszokból tevôdik össze.
Természetesen az alapösszefüggések más formában is felírhatók. Most azt gondoljuk, hogy a bemenô jel az alkatelemekre jutó feszültség és kimenetként az elemen átfolyó áramot keressük.
![]()
Utalunk az Im. 2 ábrára. Ez úgy állt elô, hogy az elôzô ábra áram-feszültségét, valamint az induktivitás-kondenzátor helyét felcseréltük. - Ezt az ábrát is érdemes alaposan tanulmányozni, - persze itt az elôzôhöz képest az ok - okozat is felcserélôdik.
Az Im. 3. ábrán már kicsit bonyolultabb esetet látunk: itt egy ellenállást és egy induktivitást látunk sorba kapcsolva. Keressük azt, hogy egy fûrészrezgés alakú áram milyen feszültséget hoz létre ezen a kétpóluson. - A fenti definíciós egyenletekbôl kiindulva azt írhatjuk, hogy a feszültség
![]() Im.
3.
Im.
3.
lesz. Ez egy differenciálegyenlet, amelyet ebben az
esetben az elôzôek alapján elég egyszerûen
meg tudunk oldani, - ahogy ez az ábrán látható
is.
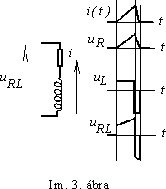
A példa egy számítógép monitor, vagy tv képcsô mágneses eltérítô áramköre. Ahhoz, hogy torzításmentes képet kapjunk, lineáris fel- és visszafutású áramjelre van szükség. - A kérdést természetesen úgy is fel lehet tenni, hogy milyen feszültségalakot kell a kétpólusra adnunk, hogy lineáris fûrészjel keletkezzen rajta. Az ábra erre ad választ: láthatóan a feszültség hullámalak eléggé "kacifántos".
Összefoglalásként azt mondhatjuk, hogy az elektromos hálózatok számításának alapvetô eszköze a differenciál- és integrálformulák megfelelô felírása és matematikai megoldása.
Fontos tudnivalók a szinuszos jelekrôl
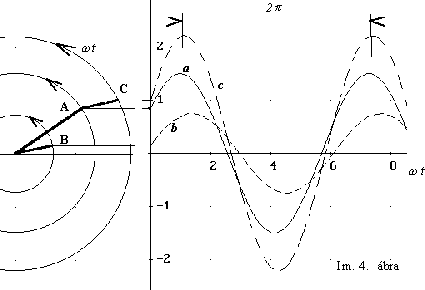
Röviden áttekintjük azt, hogy a szinuszos (koszinuszos) jelek keletkezésérôl mit kell gondolnunk a továbbiakban, - (tudatunk alá biztonsággal beépítve). Az Im. 4. ábra szerint az óramutató járásával szemben forgó "küllôk" függôleges síkra vett vetületeként képzeljük el ôket. Ha az A küllô - melynek hossza A - másodpercenként f - szer tesz meg egy teljes kört, akkor lényebében
![]() Im.
4.
Im.
4.
alakú jel keletkezik. (A 2p f értéket szokás körfrekvenciának nevezni és v -val jelölni. - Az f frekvencia reciprokát általában T -vel jelölik és periódusidônek hívják.). - A B küllô hasonlóképpen viselkedik, de most figyelembe kell vennünk az A -hoz képesti lényegi módosulást, az ún. fázistolást, fáziskülönbséget is:
![]() Im.
5.
Im.
5.
A C "küllôt" az A és B összegeként
kaptuk, vagyis A végpontjához "hozzáerôsítettük"
B -t. (Könnyû észrevenni, hogy vektoriális összegezés
történt.) - C vetülete most kiadja ![]() és
és ![]() eredôjét.
Tudatosítsuk, hogy a három szinuszgörbe maximális
értékei most nem azonos idôpillanatban következnek
be !
eredôjét.
Tudatosítsuk, hogy a három szinuszgörbe maximális
értékei most nem azonos idôpillanatban következnek
be !
Arról is kell beszélnünk, hogy miért van a szinuszos jeleknek igen nagy jelentôségük a gyakorlatban.
Megkérdezhetnénk, hogy az elektromos hálózatban - mely háztartási gépeinket, elektronikus eszközeinket, az ipari felhasználókat energiával látja el - mért használnak ilyen jeleket.
A válasz elsô része a gazdaságosságban és a célszerûségben rejlik, ugyanis vékony vezetéken csak nagy feszültség mellett (P=UI) lehet nagy teljesítményt elvezetni, viszont a nagy feszültséget csak transzformátorral lehet jó hatásfokkal átalakítani a szükséges feszültséggé. Ezek hatásfoka a mérettõl (a nagyobb általában jobb) és a beépített anyagoktól függõen kb. 80 - 99%. Azt viszont tudjuk (lásd a Transzformátor címû fejezetet) az indukciós jelenségek ismeretében, hogy a transzformátor csak váltakozó feszültséggel (árammal) tud mûködni .
A válasz második része az, hogy a generátorok - kiképzésük következtében - ilyen jelet állítanak elõ legkönnyebben. (Tudjuk, hogy egy homogén mágneses térben egyenletesen forgó síktekercsben automatikusan ilyen jelalak keletkezik. A valóságos generátorok számos tekercsbôl állnak.)
Harmadrészt pedig minden más jelforma tartalmazna felharmonikusokat (lásd a Fourier sorok címû fejezetet), ami jelentõs zavarokat okozna, illetve a veszteségek is jóval nagyobbak lennének. A nagyobb veszteség automatikusan nagyobb zavarszintet kelt a környezetben.
Az elektromos hálózatokra vonatkozó másik fontos kérdés az, hogy miért éppen 220 (egyes országokban 110, vagy 240 stb.) V effektív értékû az elektromos hálózat feszültsége? A válasz az, hogy a gazdaságossági okok a minél nagyobb, a szigetelési és életvédelmi szempontok viszont a minél kisebb feszültség mellett szólnak. (Az USA 110 V értéket választott, mivel rézben gazdag ország, "telik nekik" a vastagabb huzalokra. Azt is mondják, hogy ettôl a feszültségtôl - szerencsétlen körülményektôl eltekintve - szinte nem lehet halálos áramütést kapni.) - Az egyes régiók, kontinensek gyakorlata sok évtizeddel ezelôtt megállapodott valamilyen értékekben, ezeket csak nagyon nehezen lehet módosítani. Érdekes, hogy Anglia a 240 V értékrôl át kívánt térni két éve a 220 V-ra, de ez nem sikerült, - jelenleg 230 V a szabványos érték.
Az elektromos hálózat frekvenciájára vonatkozó kérdésre (miért használnak helyenként 50, másutt pedig 60 Herz értéket) a Transzformátorok fejezetben találunk utalást.
E rész befejezéseképpen utalunk arra, hogy szinuszos jelek esetén is lehet egyszerûen, az egyenáramnál megszokott módon számolni a pillanatnyi teljesítményt. Ha az áram és a feszültség egyaránt szinuszos és azonos frekvenciájú, akkor
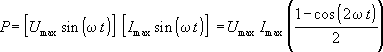 Im.
5.
Im.
5.
összefüggéshez jutunk. A koszinusz függvény egy periódusra vonatkozó átlaga nyilván zérus, így az egyetlen periódusra vonatkozó teljesítmény értéke:
![]() Im.
6.
Im.
6.
Érdemes észrevenni, hogy a kettes faktoron az áram és a feszültség "testvériesen " osztozik, hogy eljuthassunk az effektív érték definíciójához, amivel a váltakozó feszültség/áram teljesítmény számítását az egyenáramnál megszokott formában végezhetjük. Természetesen ez a meggondolás kizárólag az ellenálláson keletkezô teljesítményre vonatkozik, - tekercs és kondenzátor esetén az összefüggés bonyolultabb.
Áram- és feszültségviszonyok állandósult szinuszos jelek esetén

Tárgyalásunkat most azzal kezdjük, hogy megvizsgáljuk a lineáris alkatelemek viselkedését abban az esetben, ha a gerjesztô jel ( az "ok") szinuszos. A továbbiakban úgy gondoljuk, hogy ez a jel már elegendôen régen fennáll, - vagyis az áramkör ún. állandósult, stacioner állapotát tekintjük és nem az ún. bekapcsolási jelenséget keressük.
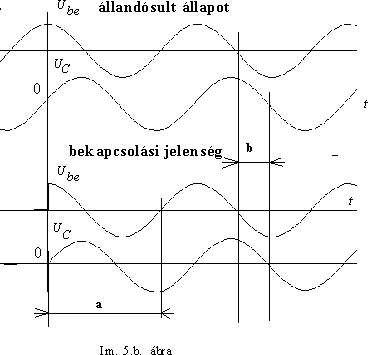
Ezek a fogalmak nagyon fontosak, értelmezésükhöz egyszerû kapcsolást választunk: egy ellenállás és egy kondenzátor soros kapcsolását (Im. 5..a. ábra). A bemenetre egy feszültséggenerátor csatlakozik, a kimeneti feszültséget a kondenzátorról vesszük. Az Im. 5.b. ábra felsô része szerint a bemeneti feszültség már régóta, jóval a 0 idôpont elôtt folyamatosan jelen volt, - ennek következtében a kimeneti feszültség is periodikus, az egyes szinuszhullámok ugyanakkora idôkéséssel, illetve fáziskéséssel (a választott értékek esetén kb. 79o ) követik egymást. Ha erre a hálózatra hirtelen kapcsolunk egy koszinuszos hullámot, akkor az ábra alsó része azt mutatja, hogy a kimeneti feszültség bonyolultabb módon változik és az állandónak tekinthetô fáziseltolódás csak bizonyos idô eltelte után alakul ki. (A bejelölt a és b szakaszok korántsem azonosak.) - Az állandósult állapot egyszerûbb, könnyebben áttekinthetô és számítható. A bekapcsolási jelenségek sokszor bonyolult tranziens függvényeket is tartalmaznak, amelyek meghatározása nehézkes. - Ne feledjük, hogy fázisszögrôl korrekt módon csak szinuszos, és mi több, csak állandósult szinuszos jelek esetében beszélhetünk. Ne legyünk azonban meglepve, ha más idôfüggvények - pl. periodikus impulzussorozatok, fûrészjelek, stb. esetén is - értelemszerûen - használják ezt a fogalmat.
A szinuszos jelek nagyon gyakoriak, számos értékes tulajdonságuk van, amelyekre részletesen kitérünk. Nagyon értékes ez a jeltípus abból a szempontból is, hogy ezeknek a jeleknek az összegezésével bármilyen jelet leírhatunk (l. Fourier sorok c. fejezet), vagyis fontos "építôkövek" módjára viselkednek.
Elôször azt az esetet tárgyaljuk, amikor egy induktivitásra szinuszos feszültséget kapcsolunk. A tekercsen átfolyó áram:
![]() Im.
7
Im.
7
Ha a feszültség ![]() formában írható fel, akkor az állandósult
áram kifejezésére az
formában írható fel, akkor az állandósult
áram kifejezésére az
![]() Im.
8.
Im.
8.
formulát kapjuk. (Vegyük észre, hogy
L![]() ellenállás dimenziójú
! )
ellenállás dimenziójú
! )
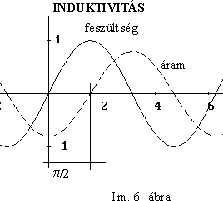
Az Im. 6 ábrán az áram és a feszültség görbéjét látjuk. Jól látszik, hogy:
- az áram idôbeli lefutása pontosan ugyanolyan, mint a feszültség hullámalakja;
- az áram azonban idôben késni látszik a feszültséghez képest, méghozzá p /2 értékkel (leginkább a pozitív maximumok elhelyezkedésébôl láthatjuk ezt).
- természetesen ez megfordítva is igaz: az induktivitáson keltett feszültség p /2 értékkel megelôzi a rajta átfolyó áramot.
Hasonlóképpen vizsgálhatjuk a kondenzátoron feszültség hatására kialakuló áramot is:
![]() Im.
9.
Im.
9.
Ha a feszültséget az elôbbihez hasonló alakúnak vesszük, akkor a
 Im.
10.
Im.
10.
kifejezéshez jutunk. (Itt is fontos tudatosítani,
hogy az 1/C![]() mennyiség
ellenállás jellegû ! ) Ezt láthatjuk az Im.
7 ábrán.
mennyiség
ellenállás jellegû ! ) Ezt láthatjuk az Im.
7 ábrán.
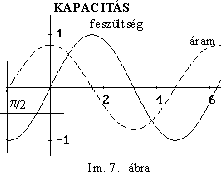
A fenti esettel analóg megállapításokat tehetünk, de most az áram látszik sietni a feszültséghez képest, de úgy is lehet mondani, hogy a feszültség késik az áramhoz képest.
Az ellenállás külön vizsgálatot nem érdemel, mert itt a feszültség és áram ugyanazon függvény szerint zajlik, és az áram valamint a feszültség között minden idôpillanatban R értéke teremt egyértelmû kapcsolatot.
Az alábbi megállapítások nagyon fontosak:
1. Induktivitás és kapacitás esetében a pillanatnyi feszültség és áram hányadosa nem állandó! Sôt, amikor az áram éppen zérus értékû, ez a hányados végtelenné válik.
Az Ohm törvény tehát pillanatnyi értékekre semmiképpen sem igaz!
2. Az áram maximális értéke és a feszültség maximális értéke között azonban egyszerû kapcsolatot találunk:
 Im.
11.
Im.
11.
Az Lw és az 1/Cw mennyiségek ohm dimenziójúak, így jogosan nevezhetôk reaktív ellenállásnak, vagy röviden reaktanciának.
3. A reaktancia értékei a frekvenciától függenek. Egy tekercs reaktanciája nulla frekvencián zérus értékû, - tehát erre a frekvenciára jelent rövidzárat (a tekercs az egyenfeszültséget/áramot "átengedi"). A kapacitív reaktancia végtelen nagy frekvencián lesz zérus, - a kondenzátor a végtelen nagy (igen nagy) frekvencián viselkedik rövidzárként.
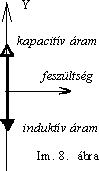
4. Az áram és feszültség közötti viszonyt igen egyszerûen ábrázolhatjuk vektorokkal. Az Im. 8. ábrán egy feszültséget, valamint induktív és kapacitív áramot ábrázoltunk irányított mennyiségekkel.
( Itt és minden más esetben arra gondoljunk, hogy ezek a vektorok az óramutatóval ellentétes irányban forognak és az Y tengelyre való vetületük adja meg a valódi idôfüggvényt.)
5. Ha az Im. 3. ábra szerinti áramkörön - ellenállás és induktivitás soros kapcsolása - folyik át szinuszos áram, akkor a kapcsoláson megjelenô feszültség:
![]()
Behelyettesítve és kicsit átalakítva:
![]()
Im. 13.
Természetesen ezt is felrajzolhatjuk vektorokkal (Im. 9. ábra). Innen egyszerûen állapíthatjuk meg U0 és f értékét:
![]() Im.
14.
Im.
14.
6. A fenti gondolatmenet sok alkatelembôl álló bonyolult áramkörre is igaz, - ezt külön részletesen nem bizonyítjuk, - könnyen átlátható. A számítások egyszerûsítésére azonban egy nagyon praktikus módszer lett általános.
Impedanciák, RLC áramkörök
Láttuk azt, hogy az egyes alkatelemeken kialakuló szinuszos feszültségek egymáshoz képesti viszonyai leginkább egy kétdimenziós vektorokra vonatkozó vektorábrán tekinthetôk át. Szerencsére rendelkezésünkre áll a komplex számok algebrája, mely számításainkat erôteljesen leegyszerûsíti és szemléletessé teszi.
Itt ennek részleteivel nem foglalkozunk, csak a legfontosabb összefüggéseket soroljuk fel a szokásos jelölésekkel. (A képzetes egységet ebben a jegyzetben j -vel jelöljük. Gyakran találkozhatunk azonban az i jelöléssel is.)
![]() Im.
15-18.
Im.
15-18.
![]()
![]()
![]()

Egy komplex számot felírhatjuk a valós és a képzetes rész összegeként, de használhatjuk az exponenciális alakot is, amelyik az abszolutértéket és fázist tartalmazza. A kétfajta megadás közötti átmenet összefüggései is ismeretesek.
(A komplex számok használatának talán a legfontosabb elônye abban rejlik, hogy a képzetes egységgel "j"-vel való szorzás mindig 90 fokkal történô elforgatást jelent, - az óramutató forgásával ellentétes irányba. Igy az induktív és kapacitív reaktanciák igen kényelmesen ábrázolhatók, értelmezhetôk. Erre látunk az Im. 10. ábrán példát. Talán külön említeni sem kell, de ez az ábra alakilag és lényegileg is hasonló az Im. 8. ábrához.)
A fentiek illusztrálására nézzünk egy, a továbbiakhoz is nagyon fontos példát. Az Im. 11. ábrán három elembôl álló kapcsolás látható. Tekintsük azt feladatunknak, hogy az eredô impedanciát kell kiszámítanunk, az alkatrészek ismeretében, - természetesen a frekvencia függvényében. (R = 10 kohm, L = 1 mH, C = 100 nF ).Az alábbi összefüggés az elsô lépést tartalmazza, melynek során hozzáadjuk a kondenzátor reaktanciájához az ellenállás-induktivitás párhuzamos reaktanciájának eredôjét - természetesen a komplex számolás szabályai szerint:

![]() Im.
19.
Im.
19.
Ezt a kifejezést kicsit átalakítjuk, hogy a valós és képzetes részét külön láthassuk:
![]() Im.
20.
Im.
20.
Jól látszik, hogy valós és képzetes rész értéke függ a frekvenciától (pontosabban a körfrekvenciától). Azért, hogy a viszonyokat jól át lehessen tekinteni, az Im. 12. ábrán megmutatjuk a számított impedancia ún. helygörbéjét.
A helygörbe két tengelyén a valós, illetve képzetes értékek szerepelnek, - a frekvencia függvényében, zérus és végtelen frekvencia között. - A komplex mennyiségekre kidolgozott számítási szabályok szerint természetesen ugyanezt a görbét akkor is megkaphatnánk, ha polár koordinátarendszerben ábrázolnánk az impedancia abszolút értékét és fázisszögét.
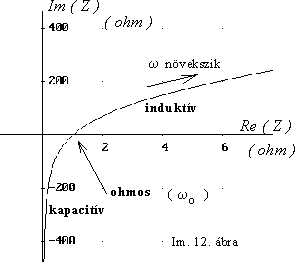
Gondoljuk csak meg: zérushoz közeli frekvencián a tekercs ellenállása elhanyagolhatóan kicsi, - az impedancia kapacitívnak adódik. Magasabb frekvencián
az impedancia induktívvá válik, extrém magas frekvencián pedig R értékû ohmos lesz - Érdekes, hogy egy meghatározott frekvencián az impedancia tisztán ohmossá válik, méghozzá elég kicsike értékûvé. (Az Im. 12. ábra a helygörbének csak egy részét mutatja!)
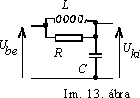
Készítsünk a fenti kapcsolásból olyan elrendezést, aminek a bemeneti kapcsaira feszültséget adunk és a kimeneti kapcsain keressük a megjelenô feszültségértéket a frekvencia függvényében. Ekkor tulajdonképpen egy feszültségosztót hoztunk létre, amelynek elemei most impedanciák (Im. 13. ábra ) A kimeneti feszültség a bemeneti feszültség függvényében:
 Im.
21.
Im.
21.
Az összefüggés elsô fele "kapásból" felírható, második felét némi egyszerûsítés után kaphatjuk. Ne feledkezzünk meg arról, hogy Uki és Ube most csak szinuszos feszültségek lehetnek !
Az Uki /Ube hányados most komplex mennyiség lesz, melyet mostantól kezdve a kapcsolás átvitelének (pontosabban frekvenciaátvitelének) nevezünk. Az átvitel tehát az
![]() m.
22.
m.
22.
kifejezés lesz. Kézenfekvô, hogy ennek a dimenzió nélküli mennyiségnek is elôállíthatjuk a helygörbéjét, az Im. 14. ábra szerint.
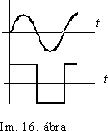

Könnyen átlátható, hogy w = 0 esetén az átvitel éppen egységnyi, igen nagy frekvenciákon pedig zérussá válik - az ábrán ezekt az értékeket szögletes zárójelben tüntettük fel. Az a tény azonban meglepô, hogy egy meghatározható frekvencián a bemenôfeszültségnek a százszorosát mérhetjük a kimeneten, vagyis a bemenôfeszültség sokszorosát. Az is eléggé furcsa, hogy az w o (f = 16.000 Hz) frekvencián a bemeneti és kimeneti feszültség között éppen 90 fok a fázistolás. (Késôbb errôl részletesebb ismereteket szerzünk: a vizsgált áramkör lényegében soros rezgôkör.)
A fenti két helygörbe egyike sem zárt. Ha a helygörbét - w és + w frekvenciahatárok között ábrázoljuk, akkor az ábrát tulajdonképpen negatív frekvenciákra is értelmezzük. Mivel az impedancia kifejezések és frekvenciaátvitelek képzetes része mindig páratlan, a valós része pedig páros függvény, ezért a negatív frekvenciákra vonatkozó ábrát a vízszintes tengelyre való tükrözéssel állíthatjuk elô. Az ilyen ábrákat Nyquist görbének is szokás nevezni.
Kérdések, feladatok
1. Rajzoljuk fel soros ellenállás és induktivitás helygörbéjét.
2. Rajzoljuk fel párhuzamos ellenállás és kondenzátor helygörbéjét.
3. Rajzoljuk fel az Im. 13. ábra szerinti kapcsolás helygörbéjét, ha az induktivitás nincs jelen (szakadás). - Mutassuk meg, hogy a görbe valójában kör.
4. Írjuk fel az Im. 15. ábrán látható kapcsolás impedanciáját és ábrázoljuk a helygörbét két esetben
a. az ellenállás értéke zérus,
b. az ellenállás értéke a megadott érték.
(Ez a kapcsolás az ún. kvarckristály elektromos helyettesítô képe.)
5. Mutassuk meg, hogy soros ellenállást és induktivitást tartalmazó áramkörben
- teljesítmény szempontjából - fontos szerephez jut az ún. cos(f ).
6. Vizsgáljuk meg, hogy az Im. 16. ábrán látható feszültségalakok melyike hoz létre nagyobb teljesítményt egy ellenálláson. (A két jel azonos csúcsértékû.)
Miért használják mégis a szinuszos jelet?
7. Az Im. 5.a. ábrához hasonló kapcsolásban (R = 10 kohm, C = 10 nF ) hogyan kell megválasztani a jel frekvenciájának értékét, hogy a fáziseltolódás nagyságára 78 fokot kapjunk? A bemenôjelnek hányadrésze érkezik meg ekkor a kimenetre?
8. Rajzoljuk fel az Im. 11. ábra szerinti kapcsolás helygörbéjét a 0 - 1 GHz frekvenciatar- tományban.