Rezgôkörök, rezonáns rendszerek vizsgálata
Az alábbiak egy nagyon fontos jelenségcsoportra vonatkozó alapvetô ismereteket tartalmazzák. Vizsgálataink során a fizikai jelenségeket, tulajdonságokot hangsúlyozzuk. Az esetenként fáradságos (bár elvileg egyáltalán nem "nehéz") matematikai részletek csak rövid utalásként szerepelnek. Határozottan javasoljuk azonban ezek elvégzését is, "kézzel-ceruzával" vagy korszerûbb segédeszközökkel, például a DERIVE, MATHEMATICA, MAPLE stb. programok felhasználásával.
Megjegyzés: folyamatos (szinuszos) rezgéseket elsôsorban az elektronikus oszcillátorok állítanak elô. Ezek aktív elemeket tartalmazó áramkörök, - amelyek esetleg rezgôköröket is tartalmaznak. A rezgôkör önmagában nem oszcillátor. A rezgôkör és oszcillátor fogalma az elektronikában nem keverhetô össze !
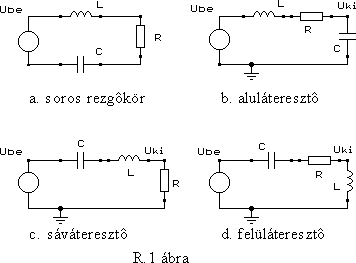
Ha olyan elektromos hálózatot készítünk, amelyikben az R-L-C elem mindegyike csak egyszer szerepel, sokfajta hálózatot tudunk rajzolni. Ezek között kiemelkedô jelentôsége van az ún. soros és párhuzamos rezgôköröknek.
Soros rezgôkörök

Az R.1.a ábra sorbakapcsolt R,L,C elemeket tartalmaz, ezt a kapcsolást nevezzük soros rezgôkörnek. A három alkatelemen megje-lenô feszültségek összege nyilvánvalóan kiadja a bemeneti feszültség értékét. Az áramkört egzaktul leíró egyenlet az alkatelemek defi-nícióit használva:
![]()
R.1.
Minden lényeges ismeretünk ennek az egyenletnek a különbözô feltételek melletti megoldásából származik.
Ha a bemeneti gerjesztés
![]()
idôfüggvény szerinti, akkor - mint ismeretes, - a differenciálegyenlettel való bíbelôdés helyett az egyes elemek reaktanciájával számolva egyszerûbben is eljuthatunk az állandósult (stacionárius) i(t) meghatározásához. Ez természetesen azonos az impedanciáknak a komplex számokkal történô megszokott kezelésével.
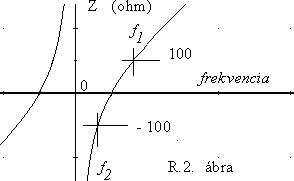
Ha megkérdezzük, hogy milyen lesz az egyes elemeken található feszültség a bemenô jel frekvenciájának függvényében, akkor mindenekelôtt meg kell határoznunk a soros rendszer eredô impedanciáját:
![]()
![]()
R.2.
Világos, hogy a zérus frekvencián felvett mínusz végtelen értékrôl csökken a képzetes rész nullára, majd növekszik plusz végtelen érték felé. (L. az R.2. ábrát, amelyet C = 100 nF, L = 1 mH érték esetén ábrázoltunk. Feltüntettük a ± 100 ohm-hoz tartozó vízszintes vonalat is, amibôl jól látszik, hogy a reaktancia abszolút értéke két különbözô frekvenciánál lesz az R ellenállással számszerûleg megegyezô.)
Jól látszik, hogy a reaktancia az ![]() körfrekvencián lesz tisztán ohmos jellegû, vagyis
ahol a reaktáns rész zérus. (Ezt a frekvenciát
hívják a rezgôkör Thomson frekvenciájának.
Az ún. rezonanciafrekvencia ezzel nem feltétlenül azonos!)
körfrekvencián lesz tisztán ohmos jellegû, vagyis
ahol a reaktáns rész zérus. (Ezt a frekvenciát
hívják a rezgôkör Thomson frekvenciájának.
Az ún. rezonanciafrekvencia ezzel nem feltétlenül azonos!)
Elsôként keressük a kimenôjel amplitúdójának változását a frekvencia függvényében, vagyis állandó amplitúdójú, különbözô frekvenciájú szinuszos bemenôjelet tételezünk fel (eredményeink természetesen állandósult állapotra vonatkoznak):
![]() illetve
illetve
![]()
H(w ) általában komplex, valós és képzetes része egyaránt van. Abszolút értéke - egy adott frekvencián - nyilván csak egyetlen szám, a fázisra vonatkozó információ hiányzik belôle. Ezt a függvényt amplitúdóátviteli karakterisztikának nevezzük, - és az áramkörök viselkedése ennek alapján válik áttekinthetôvé, érthetôvé.
Az R.1.a. ábrán csak a bemeneti feszültségforrás helyét rögzítettük. Kimeneti feszültséget a három alkatelem bármelyikérôl kaphatunk. Az R.1. b,c,d ábrák ezt mutatják. Nagyon fontos: a kimenetet nem "terheli" semmi, a terheletlen feszültséget vizsgáljuk! - A három kapcsolás, mint látni fogjuk, egy alul,- egy felül-, és egy sáváteresztô tulajdonságúnak nevezhetô szûrôt realizál. Nézzük az átviteli függvényeket: ha a kimenetet az ellenállásról vesszük, akkor az
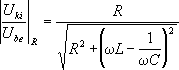
R.3.
összefüggéshez jutunk. - Az induktivitáson és a kapacitáson a kimenet a következô lesz:
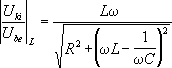
Ezeket a függvényeket érdemes ábrázolni és elnézegetni. Ehhez R = 100 ohm, L = 1 mH, C = 100 nF értékeket használtunk. - Az ábrákból több fontos következtetést tudunk levonni.
1. Az ellenálláson észlelhetô kimenet a körben folyó árammal arányos. Ez zérus értékrôl indul, eléri az Ube/R értékû maximumot, majd ismét nullára csökken. A kimeneti feszültség maximális értéke nyilvánvalóan megegyezik Ube értékével, mivel Z képzetes része a rezonanciafrekvencián zérus (R.3.ábra felsô része).
Az ábra alsó részén a két tengelyre H(w ) valós és képzetes részét vittük fel (helygörbe). Egy adott frekvenciához egy vektor tartozik, melynek nagysága természetesen megegyezik a felsô ábráról leolvasható értékkel. A vektor hajlásszöge a bemeneti és kimeneti szinuszos jelek közötti fázisdifferenciát adja meg. - Az ábra a (0 - ¥ ) frekvenciatartományt fogja át. Zérus frekvencián a fázistolás 90 fok, a fázistolás a rezo-nanciafrekvencián zérussá válik, végtelen frekvencián pedig - 90 fok értékû lesz.
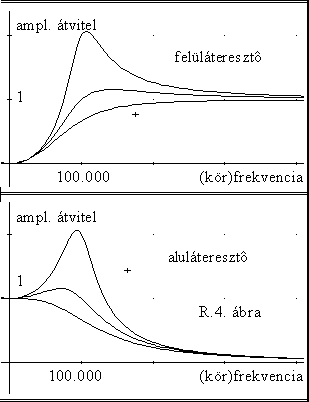
2. Az R.4. ábra az induktivitáson és a kapacitáson kialakuló frekvenciaátviteli görbéket mutatja, három különbözô R érték mellett (50, 100, 150 ohm). Látható, hogy R értékétôl függôen határozottan változik a görbe jellege: ha R "kicsi", akkor egy meghatározott frekvenciát az áramkör kiemel. Érdekes módon ez a frekvencia nem egyezik meg a rezgôkör Thomson-frekvenciájával, helye függ R értékétôl.
Az R.1.b.c.d kapcsolásokhoz tartozó három átviteli görbe egy alul-, felül-illetve sáváteresztô karakterisztikát mutat, vagyis a kondenzátoron keletkezô jel egészen alacsony frekvenciákon a bemenô jellel egyezik meg, az induktivitáson pedig extrém nagy frekvenciákon lesz csak a bemenettel azonos amplitúdójú. - Az ellenálláson csak egyetlen frekvencián egyezik meg a bemeneti és kimeneti jel amplitúdója.
3. A görbék jellege függ az áramköri elemek értékétôl. Ha C és L változatlan, akkor R csökkenésével egyre nagyobb értékû kiemelést (maximumot) kapunk az alul-, illetve felüláteresztô kapcsolások esetén. Az ellenállás növekedtével pedig az említett esetekben monoton átviteli karakterisztikát is kaphatunk.
(Ha az alul-, és felüláteresztôk amplitudóátvitelére vonatkozó összefüggések w szerinti differenciálhányadosának zérushelyeit megkeressük, akkor megkaphatjuk a szélsôértékek (maximumok, wm) helyét.
![]()
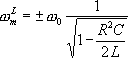 R.6.
R.6.
A képlet szerint a maximumok helyei a Thomson-frekvencia
alatt, illetve felett vannak úgy, hogy ![]() . Az is látható, hogy
. Az is látható, hogy ![]() esetén nem lesz "kiemelés", ilyenkor a maximum
helye a zérus, illetve a végtelen frekvencián lesz.)
esetén nem lesz "kiemelés", ilyenkor a maximum
helye a zérus, illetve a végtelen frekvencián lesz.)
Az áramkörök kvalitatív elemzése nagyon fontos és általában nem nehéz feladat. Az aluláteresztônél az induktivitás reaktanciája zérus(hoz közeli) frekvencián kicsi, míg a kapacitás látszólagos ellenállása nagy, - ezért az alacsonyabb frekvenciák csillapítás nélkül jutnak a kimenetre, a magasabbak pedig alig. - A felüláteresztônél a kapacitás a soros elem, - ennek reaktanciája a frekvencia növekedésével csökken, - a karakterisztika tehát fordított jellegû lesz.
Sávszélesség, jósági tényezô
Vizsgáljuk most kicsit részletesebben az
ellenálláson megjelenô (sávszûrô)
kimenet frekvenciakarakterisztikáját. Az átvitel maximuma
![]() frekvencián nyilván
egységnyi. Az átvitelt leíró összefüggés
azonban azt sugallja, hogy keressük meg azokat a frekvenciákat,
amelyeknél a reaktancia értéke (a zárójeles
kifejezés) éppen megegyezik R értékével.
Az átvitel ilyenkor
frekvencián nyilván
egységnyi. Az átvitelt leíró összefüggés
azonban azt sugallja, hogy keressük meg azokat a frekvenciákat,
amelyeknél a reaktancia értéke (a zárójeles
kifejezés) éppen megegyezik R értékével.
Az átvitel ilyenkor ![]() nagyságú, vagyis -3 dB értékû lesz. (Emlékeztetni
szeretnénk arra, hogy a frekvenciahatárok definíciói
a kényelmes, könnyen elvégezhetô számításokat
célozták meg. Ilyen értelemben pedig
nagyságú, vagyis -3 dB értékû lesz. (Emlékeztetni
szeretnénk arra, hogy a frekvenciahatárok definíciói
a kényelmes, könnyen elvégezhetô számításokat
célozták meg. Ilyen értelemben pedig ![]() az eddigiek alapján kellemes, "kerek" számnak tûnik.)
Két egyenlet gyökeit kell megkeresnünk:
az eddigiek alapján kellemes, "kerek" számnak tûnik.)
Két egyenlet gyökeit kell megkeresnünk:
![]()
![]() R.7.
R.7.
A számításba veendô gyökök:
![]()
![]() R.8.
R.8.
Vegyük e két frekvencia különbségét,
vagyis határozzuk meg "az átviteli sáv szélességét".
Arra az eredményre jutunk, hogy ![]() . Ha ezt a sávszélességet a soros kör rezonanciafrekvenciájához
viszonyítjuk, akkor a
. Ha ezt a sávszélességet a soros kör rezonanciafrekvenciájához
viszonyítjuk, akkor a
![]() R.9.
R.9.
összefüggéshez jutunk. Q-t az áramkör jósági tényezôjének nevezik és nagyon gyakran használják rezgôkörök jellemzésére. Mivel a rezonanciafrekvencián az induktivitás és a kapacitás pontosan ugyanakkora abszolút értékû reaktanciát képvisel, azt is írhatjuk, hogy
![]() R.10.
R.10.
Úgy is fogalmazhatunk, hogy a rezgôkör jósági tényezôje a rezonancia-frekvencián a reaktáns elemek által képviselt reaktáns ellenállásnak és a valós, soros ellenállásnak a hányadosa.
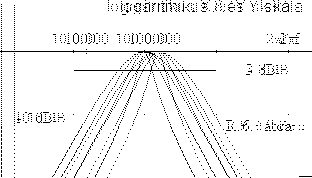
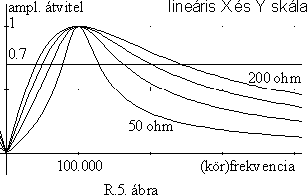
Ha a soros kör jósági tényezôje nagy (pl. azért, mert R értéke elegendôen kicsi), akkor az átviteli sáv szélessége kicsi lesz. Ilyenkor a soros kör erôsen "szelektív" hatású, csak a rezonanciafrekvencia köz-vetlen közelét "engedi át". - Ha jósági tényezô kicsi, a görbe széthúzódik, szelídebb lejtésû, lankásabb oldalai lesznek. Ezt láthatjuk az R.5. ábrán. Ez az ábra lineáris frekvencia skálával készült. Számunkra azonban többet mond az R.6. ábra, amelyik Bode diagram. (A lineáris ábrával szemben ez frekvenciában szimmetrikus!)
Valós, huzalból tekercselt, esetleg vasmaggal is ellátott induktivitásokból 2 - 100 közötti jósági tényezôjû köröket lehet készíteni. Nem szabad ugyanis megfeledkezni arról, hogy a huzalok óhatatlanul soros ellenállást is jelentenek (hacsak nem szupravezetô anyagokkal dolgozunk). A tekercsek - különösen magasabb frekvenciákon - elkerülhetetlenül sugároznak, ami energiaveszteséggel jár. Ez pedig egy újabb ellenállás megjelenésével vehetô csak figyelembe. - Még egy kellemetlen hatás: magasabb frekvenciákon az elektromos tér a vezetékek felületére "szorul" (amit skin-effektusnak neveznek), ez pedig az effektív huzalkeresztmetszetet csökkenti, vagyis az ellenállást növeli.
Ugrásfüggvény átvitel
Nagyon érdekes és fontos ismeretekhez jutunk, ha megvizsgáljuk azt az esetet, amikor a bemeneti feszültséggenerátor nem szinuszos jeleket ad, hanem egy ugrásfeszültséget, lépcsôfüggvényt. Azt képzeljük, hogy u(t) negatív t értékekre zérus, a t = 0 idôponttól kezdve pedig értéke állandó Uo.
Az R. 1. összefüggés szerinti differenciálegyenlet ebben az esetben is megoldható matematikai ismeretek alapján, - ebbôl az áram idôbeni viselkedését kapjuk meg. Az áram ismeretében az egyes elemeken létrejövô feszültség már könnyen kiszámítható. (Meg kell azonban jegyezni azt, hogy az ilyen jellegû feladatok megoldásának kényelmes, jól járható útját jelenti a Laplace transzformáció. )
Az 1.c. ábra szerinti kapcsolás kimeneti feszültsége az alábbi - általános -formában írható fel:
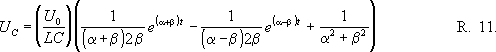
ahol
![]()
Az alkatelemek viszonyától függôen három érdekes esetet lehet megkülön-böztetni:
1. Ha b kifejezésében a gyök alatti mennyiség pozitív, akkor (a + b ) valamint (a - b ) különbözô értékû, valós negatív számok lesznek. A kimeneti jel idôfüggô része két csökkenô exponenciális idôfüggvény különbségeként áll elô.
2. Ha R értékét folyamatosan csökkentjük, akkor b egyre kisebb lesz és (a + b ), valamint (a - b ) értékei folyamatosan közelítenek egymáshoz. Ha elérjük az
![]()
"kritikus ellenállás" értéket, akkor a két érték egybeesik. Ekkor a kimeneti idôfüggvény az alábbi alakú lesz:
![]()
3. Ha R tovább csökken, akkor b képzetessé válik. A kimeneti idôfüggvény ez esetben exponenciális és szinuszos jelek kombinációjából áll elô. Az exponenciális szakaszt a szabja meg, míg a szinuszos jel frekvenciáját b determinálja. Feltûnô, hogy a rezgôkör jelenlétére jellemzô frekvencia - nullától különbözô R értékeknél - mindig kisebb, mint a Thomson frekvencia.
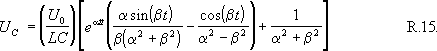
Az R.7 ábrán az egységnyi ugrásfeszültség hatására bekövetkezô kimeneti jeleket látjuk, - az ellenállás értéke természetesen változik. Az áramkör felépítésébôl következik, hogy a kimeneti jelnek - egy idô múlva - meg kell egyeznie a bemeneti jel értékével.
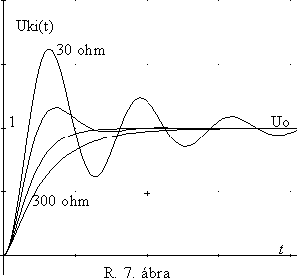
Az ábra azt mutatja, hogyha az ellenállás nagyobb, mint a kritikus érték, akkor a kimenet "lomhán" felkúszik végleges értékére. - Ha az ellenállás éppen a kritikus nagyságú, akkor a kimenet viszonylag gyorsan, de még túllendülés nélkül éri el állandósult állapotát. - A kritikus ellenállásértéknél kisebb értékeknél azonban egy új jelenség lép fel: a kimeneten csillapodó amplitúdóval "lengések" jelennek meg. Ilyen esetben a kimeneti jelen ún. túllövések keletkeznek, amelyek sokszor zavaróan hatnak. Érdekes módon e lengések frekvenciája R értékétôl is függ.
(A vizsgált soros rezgôkör differenciálegyenlete hasonlatos egy rúgóból, tömegbôl és egy veszteséges - pl. súrlódó - elembôl álló mechanikai rendszer differenciálegyenletével. Ez utóbbi rendszer viselkedésével kapcsolatosan számos személyes tapasztalatunk lehet. Ilyen például az autókba beépített lengéscsillapító: egy jó szerelô erôteljesen lenyomja a gépkocsi sarkát, majd hirtelen felengedi és azt figyeli, hogy eredeti helyzetét lengés nélkül éri-e el a kocsi. - Az élelmiszerboltokban régebben használatos mérlegek mechanikai rendszere nem kritikusan csillapított volt, - ezért igyekeztek az eladók a mérendô tárgyat "rádobni" a mérlegre és gyorsan leolvasni, majd lekapni, - hogy az elsô túllövés értékével arányosan megnövelt összeget húzzanak ki pénztárcánkból.)
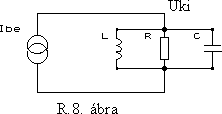
Párhuzamos rezgôkörök
Az R.8. ábrán a párhuzamos rezgôkör vázlatát láthatjuk. A soros rezgôkör bemenôjele feszültség volt, itt csak áramgenerátor szerepelhet bemenetként, mert feszültséggenerátor esetén zérus és végtelen frekvencián végtelen nagy áram folyna.
A soros kör árama (mely közös volt az összes alkatelemen):
![]() R.16.
R.16.
a párhuzamos kör kimeneti feszültsége (szintén közös az összes alkatelemre)
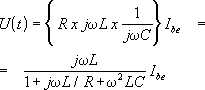 R.17.
R.17.
Az R.16. és R.17. összefüggések
matematikailag azonos szerkezetûek, aminek az az oka, hogy míg
a soros körnél az elemeken mérhetô feszültségek,
addig a párhuzamos körnél az elemeken folyó áramok
összegezôdnek, és így egymás megfelelôi.
Az is látszik, hogy az ![]() Thomson-frekvencián a kimeneti feszültség
Thomson-frekvencián a kimeneti feszültség ![]() nagyságú lesz, vagyis a bemeneti áram állandósága
mellett R értékével folyamatosan nô. Az R-rel
párhuzamosan kötött L és C rezonanciafrekvencián
végtelen nagy ellenállást jelent!
nagyságú lesz, vagyis a bemeneti áram állandósága
mellett R értékével folyamatosan nô. Az R-rel
párhuzamosan kötött L és C rezonanciafrekvencián
végtelen nagy ellenállást jelent!
A párhuzamos rezgôkör részletes vizsgálatát nem végezzük el, - a soros kör elemzéséhez hasonló módon kell eljárni. Eredményeink kvalitatíve meg fognak egyezni.
Egy fontos különbségre azonban fel kell hívni a figyelmet. Ha rezgôkör jósági tényezôjét határozzuk meg, akkor - szemben a soros körnél tapasztaltakkal - most azt kapjuk, hogy
![]() R.18.
R.18.
Csatolt rezgôkörök
Röviden foglalkozunk a csatolt rezgôkörök viselkedésével is, mert ez fontos fizikai-technikai tényre hívja fel a figyelmet.
Elemi mechanikából ismeretes, hogy ha két azonos hosszúságú ingát egymással lazán csatolunk és így állapotuk kölcsönösen befolyásolja egymást, akkor az egyik inga kitérései az idô függvényében az R.9. ábra szerint alakulnak. Azt is tudjuk, hogy
a rendszer energiája "ide-oda leng" a két inga között. - Az R.9. ábra szerinti jelalak nem az említett ingák mozgásának szimulációjából jött létre, hanem mechanikából szerzett ismereteink alap-ján két egymáshoz közeli frekvenciájú szinuszos rezgést szuperponáltunk. Az R.9. ábra az y = sin(20x) + sin(22x) függvényt ábrázolja.
(Felhívjuk a figyelmet arra, hogy e két rezgés eredôje látszólag olyan egyetlen frekvenciájú rezgés, amelynek az amplitúdója az idôben periodikusan változik. Ez a jelenség az ún. amplitúdómoduláció kapcsán a késôbbi- ekben még elô fog kerülni. )
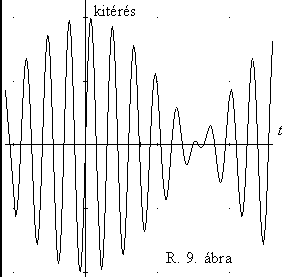
Az R.10. ábra két csatolt párhuzamos rezgôkört mutat. A felsô ábrán a csatolást a két tekercs egymáson átfûzôdô mágneses tere biztosítja ( kölcsönös induktivitás, 'k" csatolási tényezôvel). Az alsó ábrán a két tekercs között nincs mágneses kapcsolat, a két
rezgôkörnek van azonban egy közös eleme, a C-vel jelölt kapacitás. Nyilvánvaló, hogy minél kisebb ez a kapacitás, a két kör közötti kapcsolat annál szorosabb (végtelen nagy kapacitás esetén az elsô kör elektromos változásaiból semmi sem kerül át a második körre).
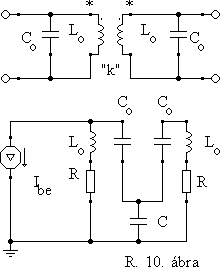
Az R.11. ábra a kapacitívan csatolt rendszer frekvenciaátviteli görbéit mutatja, ha bemenetként egy áramgenerátort használunk, kimenôjelként pedig az R-L elemeken mérhetô feszültséget mérjük, természetesen különbözô C értékek esetén. A görbékbôl elég érdekes következtetéseket tudunk levonni:
- ha a csatolás laza, akkor az átviteli görbe a rezgôkör rezonanciagörbéjére emlékeztet (a),
- szorosabb csatolásnál a görbe kezd kiszélesedni (b),
- a (c) görbe különös figyelmet érdemel: ennek sávszélessége jóval nagyobb, mint az egyedülálló rezgôköré,
- szoros csatolásnál a rezonan-ciagörbe "felhasad" és két maximuma lesz (d). A csúcsok közötti távolság és közöttük lévô völgy bemélyedése a csatolás növe-kedésével növekszik.
Híradástechnikai szempontból külö-nös jelentôsége van a c. típusú görbének. Ez ugyanis arra utal, hogy viszonylag széles átviteli sávot tudunk így elérni, - a sávon kívül pedig az átvitel meredeken csökken. Nem véletlen, hogy mindennapi rádióink és tévé-vevôink ún. középfrekvenciás erôsítô fokozataiban laza induktív csatolású hangolt rezgôköröket alkalmaznak.
Feladatok:
1 Rajzoljon egy-egy R,L,C elem felhasználásával különbözô kétpólusokat ! Hány független kétpólus hozható így létre?
2 Bizonyítsa be, hogy az R3. ábra alsó részén látható görbe kör.
3. C és L értéke adott. Mekkora ellenállás kell ugyanakkora Q-hoz soros és párhuzamos rezgôkör esetében?
4. Egy párhuzamos rezgôkör változtatható hangoló kapacitása 500 pF, induktivitása akkora, hogy a Thomson-frekvencia 500 kHz legyen. A rezonanciagörbe szélessége 4.5 kHz. Mekkora a rezgôkör jósági tényezôje? - Mekkora lesz a rezonanciafrekvencia, ha a kondenzátor értékét 50 pF-re csökkentjük? Ha az R ellenállás nem változott, mekkora lesz most a rezonanciagörbe szélessége? (közép-hullámú rádióvevô hangolása.)
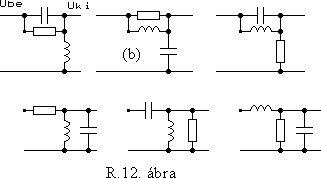
5. Adott hat darab kétpóluspár (négypólus), amelyek mindegyikében L = 1 mH, C = 100 nF, R = 100 ohm található. ( R. 12. ábra )
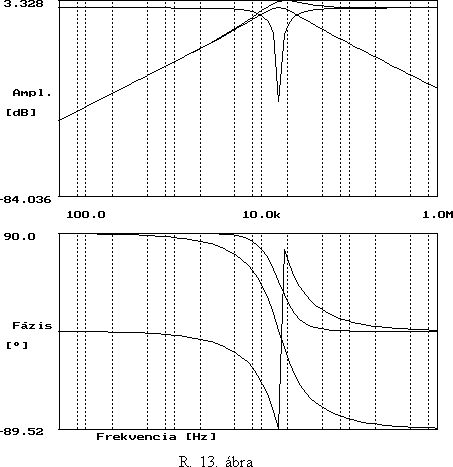
a. Az R.13. ábrán ezek közül háromnak a Bode diagramja látható. Az amplitúdó- és fázisdiagramok vizsgálata alapján azonosítsa az áramköröket.
b. Rajzolja fel kvalitatíve a másik három kétpóluspár Bode diagramját.
6. Rkrit értéknél hogyan néz ki az R12.b.ábra szerinti aluláteresztô kapcsolás amplitú-dóátviteli karakterisztikája? Van itt frekvencia kiemelés?
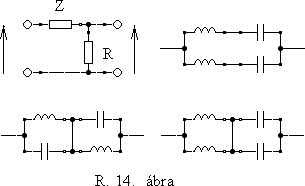
7. Az R.14. ábrán Z - R elemekbôl álló feszültségosztó rajza található. Z helyére helyezze be a felrajzolt Zi kétpólusokat és határozza meg
- kvalitatíve az amplitúdóátviteli görbéket,
- kvantitatíve a rezonancia (Thomson)-frekvenciákat és az átviteli sávszélességet.
Melyik kétpólus "kakukktojás"?
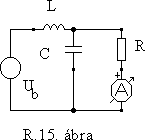
8. Az R.15. ábrán látható elrendezés arról nevezetes, van olyan frekvenciájú bemenôjel, amelynél az R ellenálláson átfolyó áram független R értékétôl. (Ezt a furcsa jelenséget Boucherot paradoxonnak nevezik.) Bizonyítsa be a fenti állítás igaz voltát
a. a szokásos impedancia-számításokkal,
b. a Norton tétel alkalmazásával.
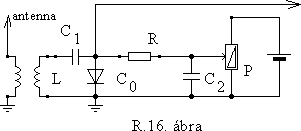
9. Az R.16. ábra olyan, feszültséggel hangolható rezgôkört mutat, amihez hasonló gyakran szerepel URH sávú rádiókban, TV készülékekben.
Értelmezze az áramkört és minden kapcsolási elemérôl állapítsa meg annak funkcióját.
11. Behelyettesítéssel mutassa meg, hogy az R.11. szerinti idôfüggvény lehet az R.1. egyenletnek megoldása.
12. Az R17. ábrán látható RLC soros rezgôkör egy 12 V-os egyenfeszültségforráshoz csatlakozik. A kapcsolót meghatározott idôpontban zárjuk, majd egy másik idôpontban nyitjuk.
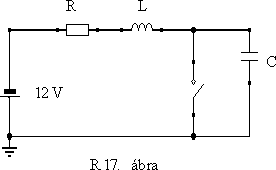
Az R18. ábrán láthatjuk a kapcsolón átfolyó áram idôbeni lefutását (pöttyözött görbe), valamint a kapcsoló nyitása után a kondenzátoron kialakuló feszültség alakját. - Értelmezze a jelalakokat és racionálisan gondolkodva igazolja, hogy azok csak ilyen jellegûek lehetnek.
(Az áramkör az autók klasszikus gyújtó áramköre. Az ábrán jelölt induktivitás egy transzformátor primer tekercse, a szekunder menetszáma igen nagy, - ez biztosítja a gyújtáshoz szükséges nagyfeszült-ségû szikrát.)
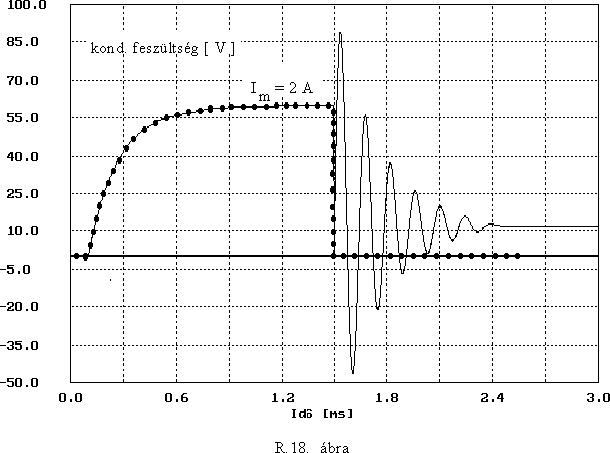
13. A fenti feladat jelalakjainak ismeretében határozza meg - közelítô pontossággal - a kapcsolási elrendezés alkatelemeinek értékét. (A kapcsoló ideális.)