Egyszerû áramkörök bistabil multivibrátorokkal

6.10.1. ábra

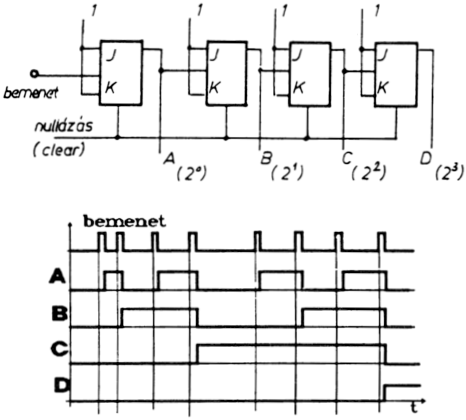
A bináris számláló elõbbi változata elõre felfelé számolt: a 6.10.2. ábrán látható áramkör az ún. visszafelé számláló. Ennél felhasználjuk, hogy bináris visszafelé számlálásnál a következõ helyiértékben akkor kell változást elõidézni, ha az elõzõ helyiértékben logikai 0 - 1 átmenet jön létre.

6.10.2. ábra

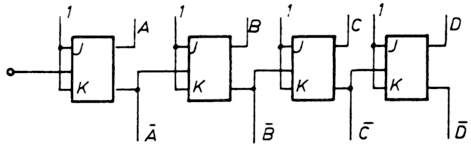
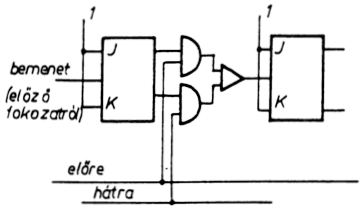
A 6.10.3. ábrán a két áramkör kombinációjaként bináris oda-vissza számláló egy fokozatát látunk. (Az irányt kijelölõ vezeték állapotától függõen a következõ fokozatra jutó jel vagy a direkt, vagy az invertált kimenetrõl jut tovább.)

6.10.3. ábra

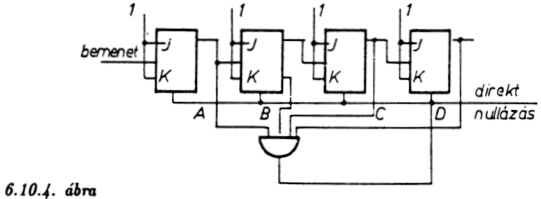
Gyakran van szükség olyan számlálóra, mely nem kettes számrendszerben számol, hanem például tizenhármasban. Ezt úgy lehet megvalósítani, hogy (lásd 6.10.4. ábra) a tizenharmadik beérkezõ impulzus után a számláló kapcsolást nullázzuk. Ennek legegyszerûbb módja egy alkalmasan megválasztott ÉS áramkörön alapul: ez detektálja az ABCD=1011 állapotot és a kimenete a direkt Reset áramkörön keresztül nullázza a bistabilokat. Ez az eljárás tulajdonképpen univerzálisnak tekinthetõ: bármilyen számláló tartalom detektálható ily módon, tehát ún. "n" alapú számláló kapcsolást állítottunk elõ.

6.10.4. ábra

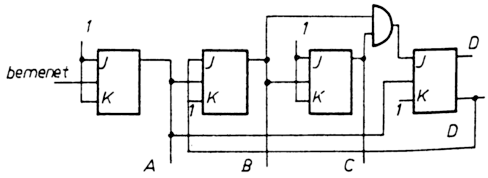
A tízes számrendszerben számláló kapcsolásoknak kiemelkedõ szerepük van, ezért számos különbözõ áramkört találtak ki speciálisan erre a célra. A 6.10.5. ábrán egy BCD (binary coded decimal) számlálót látunk. Ez tíz egymástól eltérõ állapotot képes felvenni, méghozzá úgy, hogy 0-10-ig kettes számrendszerben számol, a négy bistabil multivibrátor többi lehetséges állapotát kihagyja. (Az A multivibrátor impulzusszám-felezõ, a további három szabályos bináris számláló egészen a kilencedik impulzus beérkezéséig.)

6.10.5. ábra

6.10.6. ábra

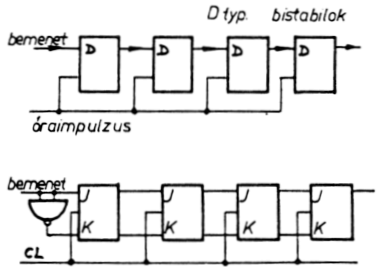
A legkülönbözõbb digitális készülékekben gyakran fordulnak elõ ún. shiftregiszterek. Ezek olyan bistabil multivibrátorokból álló kapcsolások, melyeknél a lánc minden tagjába az óraimpulzus hatására átíródik az õt közvetlenül megelõzõ bistabil tartalma. Így a tárolt információ az óraimpulzusok ütemében egy helyiértékkel továbbhalad. A 6.10.7. 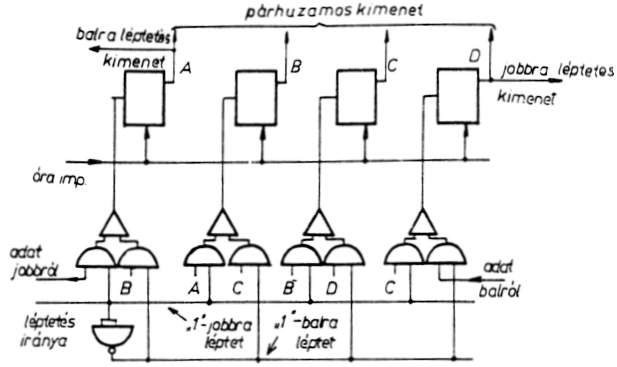ábrán D illetve JK típusú multivibrátorokkal megvalósított shiftregisztert láthatunk, a 6.10.8. ábrán pedig a mindkét irányban léptethetõ shiftregisztert mutatunk. (Természetesen a léptetés irányát egy logikai jelnek kell megszabnia.)

6.10.7. ábra

6.10.8. ábra

A shiftregiszterek igen nagyszámú feladat ellátására alkalmasak. Felhasználhatók egy igen fontos szerepkörben: soros-paralell illetve paralell-soros átalakítóként. Az idõben egymás után érkezõ bemenõ információ ugyanis egyidejûleg vehetõ ki a regiszterbõl, illetve párhuzamosan beírt információ a regiszter léptetésével annak kimenetén idõben sorosan vehetõ ki. Nyilvánvalóan jól használható a shift- regiszter digitális számítógépek aritmetikai egységében: a léptetés kettõvel való szorzásnak vagy osztásnak felelhet meg. Ha a shiftregiszter kimenetérõl az információt a bemenetre visszacsatoljuk, akkor a számlálólánc "tartalmát" az órajel "körbe pörgeti". Ez az áramkör az ún. "ring-scaler", gyûrûs számláló. (Úgy mûködik, mint egy végtelenített magnetofonszalag.)

6.10.9. ábra

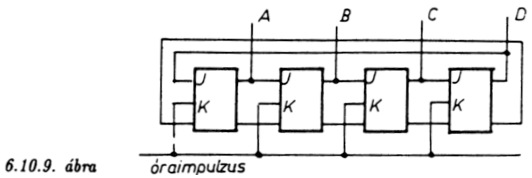
A 6.10.10. ábrán egy érdekes áramkört látunk. Itt a kimenetet invertálva vezetjük vissza a bemenetre. Az elnevezés ezután érthetõ: Moebius számlálónak hívják ezt az elrendezést. Érdekessége a kapcsolásnak, hogyha a 00000 állapotból indulunk ki, akkor pontosan 10 órajel után visszajutunk a kiinduló állapotba - ez a fura kapcsolás tehát egy decimális számláló.

6.10.10. ábra

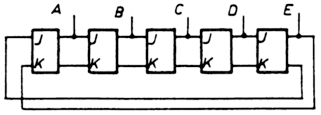
A 6.10.11. ábrán egy shiftregiszterbõl kialakított kapcsolás vázlatát láthatjuk. A bemenetet a kimenet és a - hozzá képest - késleltett kimenet egy sajátos logikai kapcsolata (XOR) szabja meg. Nézzük meg, hogyan alakul a kimenet, ha a 0000 állapotból indulunk. Könnyû belátni, hogy az órajel hatására semmi sem változik, a shiftregiszter elemei folyamatosan 0 értékûek lesznek.

6.10.11. ábra

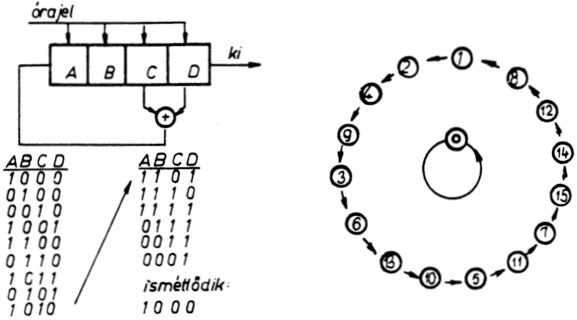
Ha azonban pl. az 1000 állapotból indulunk, akkor a rendszer állapotai változni kezdenek és 15 órajel után visszajutunk a kiinduló állapotba. (Lásd jobboldali ábra.) A változások eléggé furcsák - a kimeneti bináris értékek "összevissza" változnak. Ha ezeket az egymást követõ fej/írás értékeket valahol látnánk, joggal merülne fel bennünk az a gyanú, hogy ezek "véletlenszerûen" követik egymást. (Az ábrán látható gráfot állapot-átmeneti-diagramnak hívják.) Teljesen természetes, hogy az eredmény nem igazi véletlen, hisz egy determinisztikus rendszer generálta a kimenõ jelsõrozatot, amelyik kiméletlenül, periódikusan ismétlõdik. Nyilvánvaló az is, hogy a kimenõ sorozatban maximálisan négy 1-es szerepelhet egymás után, és legfeljebb három 0 követheti egymást. Az "igazi" véletlen sorozatokban a 0 és 1 sorozatok tetszõleges hosszúságúak lehetnek. Azt is érdemes észrevenni, hogy az n-ik és (n-1)-ik fokozat összegét - persze bináris összegét - vezetjük vissza a bemenetre. (Ennek a sajátos áramkörnek tehát van valamelyes köze a Fibonacci számokhoz is...) Természetesen vetõdik fel a kérdés, lehet-e hosszabb ún. álvéletlen jelsõrozatokat generálni az ábrán látható séma szerint, a shiftregiszter fokozatszámának növelésével. Matematikusok alaposan megvizsgálták ezt a kérdést és azt találták, hogy minden n-hez (n a shiftregiszter fokozatainak száma) lehet találni olyan visszacsatoló hálózatokat, amelyek ún. maximális hosszúságú szekvenciát állítanak elõ (vagyis a kimenõjel csak 2ⁿ-1 lépés után ismétlodik). Általában azonban nem csak két fokozatról kell viszacsatolnunk, hanem n különbözõ értékeinél esetleg többrõl is. Ezeket az értékeket XOR-oznunk kell, vagyis a bináris összeget kell elõállítanunk. Az alábbiakban megadjuk néhány n-hez, hogy a shiftregiszter melyik fokozatáról kell a visszacsatoló hálózatot táplálnunk. Az l,m,n értékek a shiftregiszternek a visszacsatolásban résztvevõ fokozatainak a számát jelölik.

n	l,m,n
6	5,6
8	4,5,6,8
16	4,13,15,16
22	21,22
24	17,22,23,24
29	27,29
36	25,36

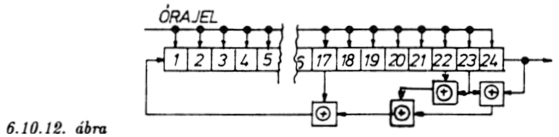
A fentiek szerint tehát egy n = 24 bistabilból álló shiftregiszterbõl a 6.10.12. ábra szerint készíthetünk maximális hosszúságú álvéletlen generátort.

6.10.12. ábra