next up previous
Következő: Tartalomjegyzék | Tartalomjegyzék | Előző: Felhasználói portok

Számítástechnika és fizika

A számítástechnika (számítógépek, computer science stb.) a fizikának és a matematikának a gyermeke, de mióta felnőtt, önállóvá vált és részben saját útját járja. Régi kötődéseitől - szerencsére - nem szakadt el, szüleit rendszeresen támogatja. Néha azonban szembe kell néznie önmagával, fel kell mérnie, honnan hová tart. Ilyenkor lényegi kérdések is felmerülnek, amelyek mind a fizika, mind a matematika alapvető fogalmait is érintik. Fontos kérdés például az, hogy melyek azok a fizikai törvények, rendező elvek, amelyek korlátot szabnak a fejlődésnek. Ilyen megszorítások nyilván léteznek, hiszen elegendő, ha a fénysebesség korlátos voltára gondolunk. No, de meddig lehet a logikai áramkörök sebességét fokozni, mekkora a lehető legkisebb méretű tároló-cella, mi az a legkisebb energia, amit a számítások nem nélkülözhetnek? Valami válaszra feltétlenül szükségünk van, mert a társadalmi, tudományos és piaci igények egyaránt a számítástechnika fejlesztését sürgetik. Számos olyan feladat létezik, amelyek megoldásához a jelenlegi lehetőségek nem elégségesek. Csak példaképpen: a meteorológia óriási számítástechnikát tudna lekötni. Mérsékelt felbontású, az egész Földre kiterjedő időjárási modell racionális viszonyok közötti működtetése mintegy ezerszer akkora számítógép-sebességet kíván, mint amivel a jelenlegi leggyorsabb gépek rendelkeznek. Ugyancsak komoly kihívást jelent az egyre növekvő mennyiségi és minőségi igénnyel jelentkező képfeldolgozás is. A tudományos kutatások számítógép éhségét pedig talán meg sem kell említenünk. Érdemes és érdekes szembenézni azzal a problémával, hogy mekkora lehetőségek rejlenek még a fizikában a számítástechnika számára. Elsőként az energia kérdését vizsgáljuk meg. A digitális számítógép olyan gép, mely energia disszipáció árán matematikai munkát végez. Régóta foglalkoztatja a fizikusokat, vajon van-e ennek a termodinamikai folyamatnak valamely természetes korlátja, mely a tényleges fizikai megvalósítástól függetlenül valamifajta határt szab. Sokan idézik Neumann Jánost, aki 1949-ben egy előadásában már arról beszét, hogy egy T homérsékletű számítógép elemi döntéseinél, elemi információátviteli folyamatainál legalább $kT\ln 2$ energiát kell felhasználnunk ( $\simeq 3\times 10^{-21}$ J szobahomérsékleten). Bár az állítás egzakt igazolása elég nehézkes, az azonban, hogy a legkisebb energia a kT értékkel arányos, könnyen átlátható. A jelenlegi számítástechnikai eszközök még igencsak távol állnak ettől az értéktől. Gondoljuk a bistabil multivibrátorokra: ezek még akkor is fogyasztanak energiát, amikor "semmit se csinálnak". Valamivel jobb a helyzet a mágneses információtárolásnál, a CMOS áramköröknél stb. Itt energiára csak beíráskor, törléskor van szükség. Ezek az elemek természetesen még makroszkópikus méretűek, nem csoda, ha sok energiát igényelnek. Idegsejtjeink, amelyeket igen jó hatásfokúaknak tartunk, 1011 kT energiát fogyasztanak kisülésenként, sokkal kevesebbet, mint eddigi elektronikus áramköreink. Az eddig ismert leghatékonyabb számítógép - a DNS reprodukció - kb 100 kT energiát használ lépésenként. A Neumann által említett határ tehát még messze van, noha ma már sikerül egyetlen elektront csapdába ejteni úgy, hogy ezzel egy bináris tárolót lehet létrehozni. Persze itt a fizikai körülmények - pl. extrém alacsony hőmérsékletek - létrehozása és fenntartása címén kell rengeteg energiát eldorbézolni. A fizikában a számítástechnikai HI - LO értékeknek különböző energiaszintek felelnek meg (8.7.1. ábra). Gondoljuk azt, hogy a bináris információ tárolására golyókat használunk, amelyeknek energiája, vagy helyzete jelezheti az információ pillanatnyi értékét.


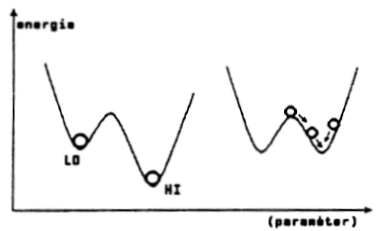
8.7.1. ábra


Ha az erőtér konzervatív, mint egyszerű modellünknél, akkor a számítás folyamatában egyszer betáplált energiát mindig visszanyerhetjük. Ha a két "gödör" azonos energiaszinten van, akkor csak a gát leküzdéséhez szükséges energiát kell közölni, amit elvben rögtön visszakapunk. Kihasználva modellünket, azt is látjuk, hogy ez bizonyos veszélyt rejt magában, mert a golyó nyugalmi helyzete körül elkezd oszcillálni. Lecsillapításához pl. surlódásra, vagyis disszipációra van szükség; tehát már a legegyszerübb esetben is energiaveszteséggel kell számolnunk. Azt is érezzük, hogy fizikai rendszerekben is sokszor jelent problémát a betáplált energia visszanyerése. A gépkocsit is fékrendszerrel látják el ahelyett, hogy a mozgási energiát valami ravasz módon helyzeti energiává, netán benzinné alakítanák vissza. Így azután megrendülés nélkül vesszük tudomásul, hogy elektronikus alkatelemeink is veszteségesek - noha elvben itt is lehetnének módszerek a bitekben rejlő energia "rekuperálására". Van azonban egy másik, sokkal súlyosabb következményekkel járó tény is. A számítás folyamata általában nem reverzibilis lépések sorozatából áll. Tudjuk azt, hogy 5+3 = 8, de ha azt látjuk, hogy az eredmény 8, nem tudjuk megmondani mely számok összegeként állt ez elő. A számítástechnika elemi műveleteinek többsége nem megfordítható, vagyis nem reverzibilis. Ha például valamit nullázunk, a művelet elvégzése után nem tudjuk megmondani, hogy mi volt az eredeti állapot. Ha a jelek egy ÉS áramkörön haladnak keresztül, a helyzet hasonló lesz: a kimenetből itt sem tudunk egyértelműen visszakövetkeztetni a bemeneti állapotokra. A logikai függvények tehát nem az egy-egy, hanem a sok-egy leképzést valósítják meg, vagyis a kimeneti állapotok száma kisebb lesz, mint a bemenetieké. Ez pedig óhatalanul entrópiaváltozást, mégpedig csökkenést jelent. Ha a számítógéphez a működtető telepet is hozzáértjük, akkor az így meghatározott zárt rendszer entrópiacsökkenésének valahol hőhatásként kell megjelennie. Ez annyit jelent, hogy a számítási folymat hőtermeléssel jár, vagyi szükségképpen disszipatív. Vegyük észre, hogy ezen gondolatmenet szerint számításaink mindig energiaveszteséggel fognak járni. Ravasz fizikusok azonban feltették azt a kérdést, hogy nem lehet-e olyan logikai áramköröket, vagy logikai modelleket szerkeszteni, amelyek azon túlmenően, hogy velük mindenfajta logikai függvény megvalósítható, ezen kívül reverzibilisek is. 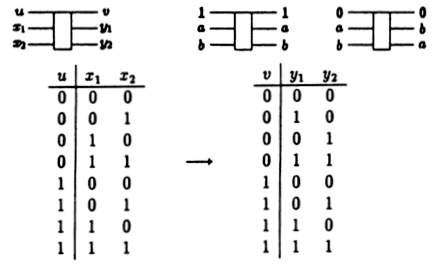Fredkin (1982-ben) kitalált egy "áramkört", amelyik ezeknek a feltételeknek eleget tesz. A logikai kapu és igazságtáblázata a 8.7.2. ábrán látható. Ha az u vezetékre 1 érkezik, akkor x1 és x2 változatlanul jut a kimenetre. Ha azonban u értéke 0, akkor a két vezeték felcserélődik. Vegyük észre, hogy az igazságtáblázat most egy-egy leképzést valósít meg.





u x1 x2
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
$\qquad \longrightarrow \qquad$
v y1 y2
0 0 0
0 1 0
0 0 1
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1


8.7.2. ábra


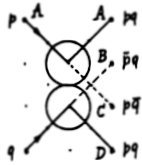
A látszólag egyszerű elrendezés nagyon sok lehetőséget rejt magában. A 8.7.3. ábrán az OR (a), a NOT (b) és a kimenet többszörözés (c) funkcióit láthatjuk, valamint azt, hogyan lehet egy speciális JK bistabil multivibrátort megvalósítani (d). (Ez utóbbi ábrán a kis háromszög az egység-időnyi késleltetést reprezentálja.)


8.7.3. ábra


Azt is el kell mondanunk, hogy a Fredkin kapunál egyszerűbb meggyőző modellek is léteznek, amelyek a reverzibilis számítási lehetőség gondolatát támogatják. Ezek közé tartozik a "golyó" logika (8.7.4. ábra). Képzeljük el, hogy két rugalmas, azonos átmérőjű golyót indítunk azonos sebességgel, meghatározott függőleges távolságban egymástól, a vízszinteshez képest 45 fokkal felfelé illetve lefelé. A golyók valahol a rácshálózat egy pontján rugalmasan ütköz(het)nek. (A szabályok eléggé kézenfekvőek: a golyók átmérője a rácsosztásnak megfelelő, sebességük azonos, ütközéskor az elemi fizika szabályai érvényesek.)


8.7.4. ábra


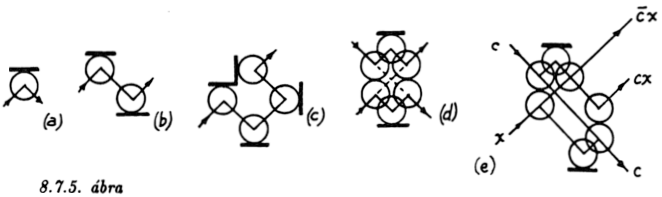
Jól látható, hogy az ütközés után, a kimeneti függőleges bizonyos pontjain a golyók megjelenése - vagy meg nem jelenése - meghatározott logikai kapcsolatot reprezentál. A rendszerben elhelyezhetünk rugalmas reflektorokat is, így a 8.7.5. ábra szerint igen változatos funkciókat tudunk létrehozni. Az (e) változat különösen érdekes: hasonlít az előbb tárgyalt Fredkin kapuhoz. Valójában az e szerinti kombináció ismételt felhasználásával tényleg meg lehet valósítani a Fredkin kaput. Lehet tehát egy olyan komputert tervezni, amelyiknek a bemenetén egy startjelre golyók indulnak, a kimenet pedig a bizonyos helyeken megfigyelt és detektált golyó-érkezésekből és regisztrálásokból áll. A modell legfontosabb értéke az, hogy golyók rugalmas ütközésével lehet szimulálni egy számítógép logikai funkcióit. Ez pedig nyilván megfordítható folyamat. Az előzőek alapján tehát odáig jutottunk, hogy a számítástechnika által indukált entrópiacsökkenés - elvben legalább - megszüntethető, és lehetne olyan számítógépet szerkeszteni, amelyik hosszútávon nem igényel energia befektetést. Ennek a megállapításnak eléggé nagy jelentősége van az élő szervezetek alkatelemeinek másolásánál, felépítésénél, kémiai/biológiai adatfeldolgozásánál.


8.7.5. ábra


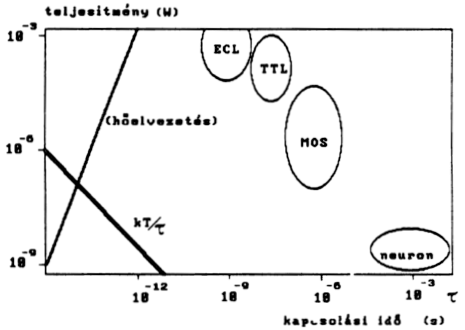
A továbbiakban néhány példán illusztráljuk, hogy egyes fizikai törvények miképpen limitálják a számítástechnikát, illetve azt, hogy a fizikusok miként gondolkodnak, érvelnek ebben a tárgykörben. Nézzük meg először azt, milyen következményei vannak annak, hogy egy melegedő felületről csak korlátos mennyiségű hőt tudunk hűtéssel eltávolítani. Nagyságrendileg helyes becslés szerint egy négyzetcentiméternyi felületrol Ph = 10 W-ot lehet normális muszaki körülmények között elszállítani. (Ezt most amolyan természeti állandónak tekintjük.) Ha egy elemi logikai egység disszipációja P0, akkor a két mennyiség hányadosaként megkaphatjuk, hogy a felületen a kérdéses kapuból mennyi helyezhető el. Ennek négyzetgyöke megadja az 1 cm hosszúságon elhelyezhető kapuk számát. A kapuk között - optimista feltételezés szerint - fénysebességgel terjednek a jelek. Ha azt mondjuk, hogy kommunikálni csak egymás melletti kapukkal kell, akkor az ehhez szükséges idő

\begin{displaymath}\tau \simeq {1\over c}\sqrt{ {P_0\over P_h}}\quad. \end{displaymath}

Ezt az összefüggést a 8.7.6. ábrán tüntettük fel. Az ábra vízszintes tengelyén azt az időtartamot tüntettük fel, ami a logikai kapcsolások elvégzéséhez szükséges. Ezt kapcsolási időnek neveztük, kissé pontatlanul, mert az előbbi gondolatmenet szerint csak terjedési idővel számoltunk. Olyan ábrát akartunk előállítani, amelyiken a sebeség és teljesítmény viszonyok egyszerűen áttekinthetők. Az ábra függőleges tengelyén a logikai elemek teljesítményigénye szerepel. Ebbe az ábrába be tudjuk rajzolni a kT energia-minimum hatását is, valamint feltüntethetjük jelenlegi logikai rendszereink tipikus sebesség és teljesítmény értékeit. Az ábrát érdemes figyelmesen szemlélni, és észrevenni azt, hogy bár a számítástechnika fejlődésére még van fizikai lehetőség, azonban korántsem olyan sok nagyságrendben. Ne feledkezzünk meg arról se, hogy ebbe az ábrába csak két korlátot rajzoltunk be - holott számos más is létezik. Befejezésképpen néhány különös adatot sorolunk fel. Ezek általában alapvető fizikai összefüggések elemzéséből, illetve ezek kombinációiból adódnak.


8.7.6 ábra


Sokan foglalkoztak az anyag/tömeg számítástechnikai kapacitásának meghatározásával. Kiszámították, hogy a hidrogénatom tömege $2\times 10^{23}$ bit/sec sebességű információfeldolgozást tesz lehetővé. Kicsit szinesebb példa: egy földméretű és életkorú komputer anyaga kb. 1093 bit feldolgozását teszi lehetővé, vagyis a sakk-probléma mintegy 10120-nyi kombinációjának végigpróbálására nem elegendő. Megint másképp fogalmazva: egy proton tömege 7 bitet képes feldolgozni annyi idő alatt, míg a fény egy protonátmérőnyi utat tesz meg. Kiszámolták az 1 cm3-nyi anyagban tárolható bitek számát is: ez hozzávetőleg 1015. Ha az ilyen surun beírt infromációt 100 W teljesítménnyel olvassuk ki, akkor kevesebb mint egyetlen mikrosecundum alatt befejezhetjük ezt a feladatot.

next up previous
Következő: Tartalomjegyzék | Tartalomjegyzék | Előző: Felhasználói portok


1999-09-23