1. Bevezetés

A fénysebesség egyike az univerzális állandóknak, jelenleg ezért alapállandónak tekintjük, és értékét az SI mértékegység-rendszer c=299 792 458 m/s–ban definiálja. Az SI mértékegységrendszer ma már a távolság alapegységét a fénysebesség állandó voltára alapozva, annak felhasználásával határozza meg. Erre természetesen csak azután tettek javaslatot, miután kísérletek sokasága bizonyította, hogy az elektromágneses sugárzás terjedési sebessége vákuumban állandó. Ezekben a kísérletekben az ős-méterre alapozott távolságskálát használtak. A jelen mérés célja egy hasonló fénysebesség meghatározás hosszúság és idő mérésére visszavezetve: a mérés során egy egyszerű LC rezgőkör sajátfrekvenciája alapján határozzuk meg a fénysebességet.

Már a Maxwell-egyenleteket tartalmazó értekezésben Maxwell a fényt az elektromágneses hullám formájában képzelte el. Erre az is alapot adott, hogy 1873-ban Foucault által forgótükörrel mért fénysebessége (c=298360000 m/s) nem esett messze a Weber és Kohlrausch 1856-ban alapján, elektromos és mágneses mérésekből meghatározott c=310740000 m/s értéktől.

Tekintsük most át a fénysebesség meghatározásának gondolatmenetét: egy egyszerű síkkondenzátor és egy egyszerű légmagos tekercs induktivitásának meghatározásán keresztül.

Ha egy A felületű, egymástól d távolságra levő lemezpárra Q töltést viszünk fel, akkor a két lemez közötti térerősség értéke a Gauss-tétel segítségével könnyen kiszámítható:

E = s/e₀ = 1/e₀ Q /A

Innen a feszültségkülönbség:

U= E d = s/e₀ d= 1/e₀ d Q/A

A Q töltés és az U feszültségkülönbség aránya megadja a kondenzátor kapacitását:

C= e₀ A/d (1)

Ez a képlet természetesen csak vákuumban igaz – a jelen mérésben azonban elhanyagolhatjuk a két lemez közötti levegő hatását (Miért tehetjük ez meg?).

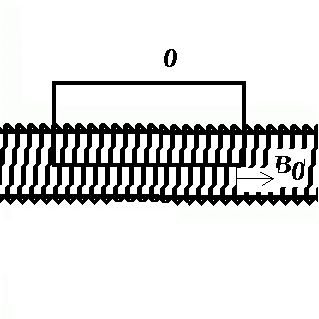
Egy l hosszúságú, r sugarú hengerre elhelyezett, hosszegységenként n átlagos menetszámú légmagos tekercs induktivitásának meghatározásához tegyük fel, hogy a tekercsben I áram folyik. A tekercs belsejében a mágneses indukció értékét az Ampère-törvény alapján kaphatjuk meg:



Integráljunk az ábrán látható kontúrra! Ha feltesszük, hogy a mágneses tér értéke a tekercsen kívül 0, belül pedig B₀ , akkor azt kapjuk, hogy a körintegrál értéke B₀ l , mivel a két, a tekercs tengelyére merőleges szakasznak nincs járuléka. A hurkon átfolyó teljes áramerősség viszont N I, azaz

B₀ = m₀ N/l I = m₀ n I

A tekercs induktivitását könnyen megkaphatjuk, ha tudjuk, hogy az I árammal átjárt tekercs mágneses terében tárolt energia megegyezik I²L/2-vel, azaz

m₀^-1B₀ ² V /2 = m₀ (n I )² p r² l /2 = I² L/2

, innen

L=p m₀ r² n² l (2)

(a képletben csak a tekercs V=p r²l térfogatát vettük figyelembe).

Ez a képlet természetesen csak vákuumban igaz – a jelen mérésben azonban elhanyagolhatjuk a tekercsben lévő levegő hatását (Miért tehetjük ez meg?).

Készítsünk rezgőkört a kondenzátorral és a tekerccsel! A rezgőkör rezonanciafrekvenciája (illetve egy periódus rezgésideje) az előzőek alapján könnyen megkapható:

2p f = (LC)^-1/2 = (p r² n² l / (m₀ e₀ ) A/d)^-1/2 = (p r² n² l A/d)^-1/2 (e₀ m₀ )^-1/2 (3)

Átrendezve:

(e₀ m₀ )^-1/2 = (4 p³ r² n² l A/d)^1/2 / T (4)

Látható módon az egyenlet három tagot tartalmaz: egy T rezgésidőt (ami pl. oszcilloszkóppal mérhető), egy távolság dimenziójú (4 p³ r² n² l A/d)^1/2 tagot, ami a geometriai méretekből meghatározató, valamint egy sebesség dimenziójú állandó mennyiséget (e₀ m₀)^-1/2 , amely megadja az elektromos és a mágneses változások terjedésének sebességet – ez pontosan az a fénysebesség, amit keresünk! Rezgőkörünkben az energia részben az induktivitás mágneses terében, részben a kapacitás elektromos terében tárolódik. Az
(e₀ m₀ )^-1/2 mennyiség azt adja meg, hogy ezek a térrészek mennyire gyorsan tudnak kiürülni ill. feltöltődni – a jelen mérési elrendezésben a vezetékeken történő késleltetés elhanyagolható (miért tehetjük meg ezt?)!

 

2. A kísérleti elrendezés

A mérési elrendezés az ábrán látható: a generátor jelét induktív módon csatoljuk a szolenoidra, és szintén induktív módon detektáljuk a maximumot az oszcilloszkóppal. Ez az elrendezés minimalizálja az oszcilloszkóp és a generátor hatását a rezgőkörre. (Milyen hatással kellene számolni a direkt csatolás esetén?)

 



 

 

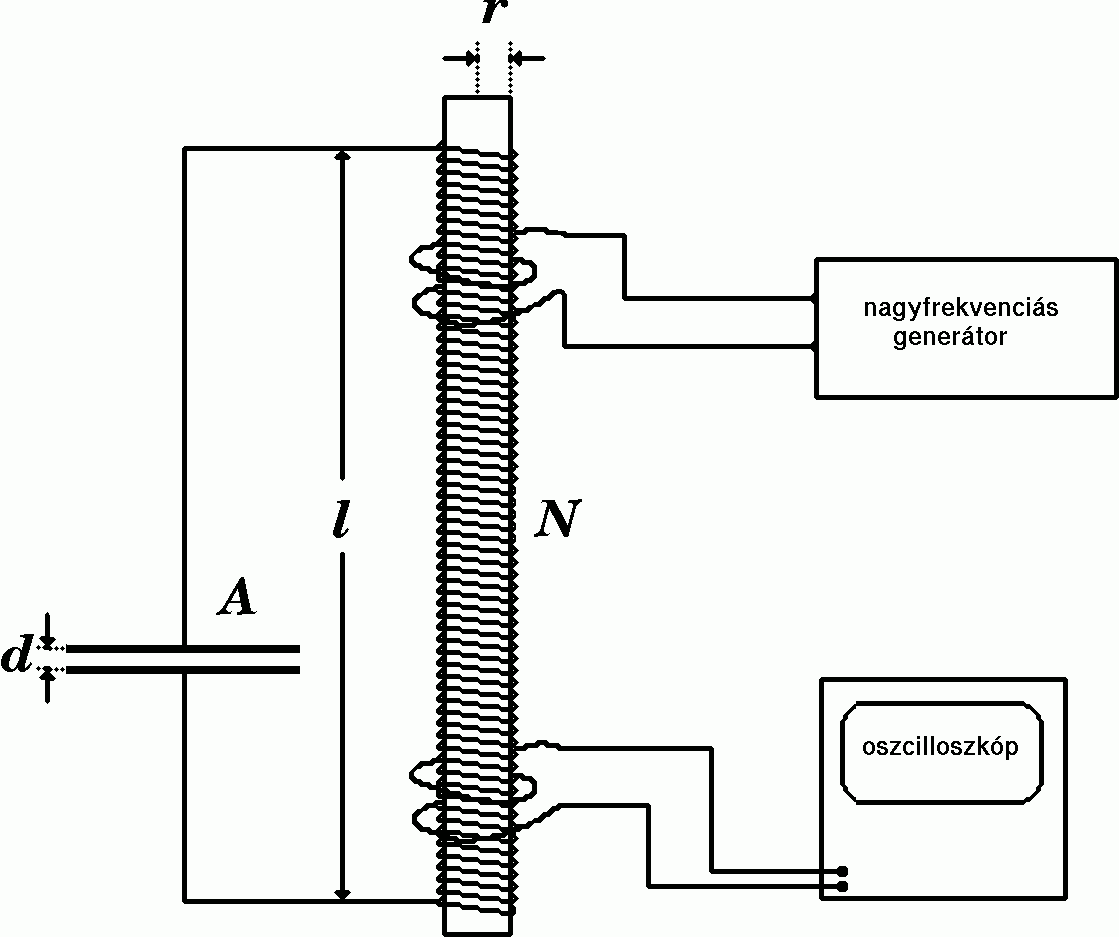
A mérés során két síkkondenzátort használunk, méreteik:

A₁=(200 +/- 1) x (250 +/- 1) mm² d=1.55+/- 0.05 mm

, valamint

A₂=(100 +/- 1) x (250 +/- 1) mm² d=1.45+/- 0.05 mm.

A tekercs 915 mm-es hosszában 1255 menetet tartalmaz, a véget is beleértve összesen 19 leágazási pontban (a nagy jelölések 100 menetszámonként vannak), sugara r=20 +/- 0.2 mm.

A C kapacitás meghatározásakor elhanyagoltuk a széleket – itt a térerősség nem lesz homogén. A pontos értékhez a geometria ismerete, valamint differenciálegyenletek pontos numerikus megoldása kellene . A számunkra érdekes pontossággal megkapható a korrekció, ha a lapok méretét a köztük lévő távolság 3/8 részével megnyújtjuk (l. Feynmann: Mai fizika, 58.10 fejezet).

Pontosítsuk most az induktivitás (2)-es képletét, és vegyük figyelembe a tekercs végének hatását is! A tekercs mindkét végén a szétnyíló B erővonalaknál a B² teljes féltérre vett térfogati integrálját helyettesítsük egy olyan, a B_homogén teret tartalmazó henger alakú térfogattal, amely keresztmetszete megegyezik a tekercs keresztmetszetével, magassága pedig a r. Az a értéke adott geometria esetén pontosan megkapható a mágneses tér (az Ampère-törvény által jól meghatározható) eloszlása alapján. Hosszú, vékony tekercsek esetén jó közelítéssel feltételezhetjük, hogy az a állandó. Az a érték valójában nem paraméter, hiszen értéke pl. numerikus integrálással megkapható, de most tekintsük ezt is a mérésből meghatározandó (illesztendő) mennyiségnek. A tekercs induktivitásának kiszámolásakor az előzőek alapján a p r²l térfogat mellé így figyelembe kell vennünk mindkét végre egy-egy effektív ap r³ térfogatot is. Így az induktivitás pontosabban az

L=p m₀ r² n² ( l +2apr)

értékkel lesz közelíthető.

 

3. Feladatok

1.) Az (e₀ m₀ )^-1/2 mennyiség azt adja meg, hogy ezek a térrészek mennyire gyorsan tudnak kiürülni ill. feltöltődni – a jelen mérési elrendezésben a vezetékeken történő késleltetés elhanyagolható. Miért tehetjük meg ezt?

3.) Adja meg a korrekciókkal a módosított (3)-as képletet , valamint a benne található numerikus paramétereket SI mértékegység rendszerben és adja meg hibájukat (vagy vegye a szélsőséges eseteket, ha még nem tanult hibaszámolást)! A képletben csak A, d, n, l, valamint c és a szerepelhet! Mivel a két kondenzátort összesen 4 féle képpen köthetjük a tekercsre (külön-külön, sorosan és párhuzamosan), ezért mind a 4 lehetőséget vegye figyelembe:

4.) A tekercsnek is vannak szórt kapacitásai. Először mindenféle kondenzátor és vezeték nélkül keresse meg ezeket a jellemző rezonancia frekvenciákat (lokális maximumok) a 100 kHz- 10MHz tartományban, és adja meg a tipikus frekvencia és (amplitúdó/generátor amplitúdó) értékeket ezeken a helyeken:

5.) A két kondenzátort összesen 4 féle képpen köthetjük a tekercsre (külön-külön, sorosan és párhuzamosan). Minden egyes kondenzátorváltozatnál mérje meg minden tekercsleágazásnál a rezonanciafrekvenciát (tipikusan a 100 kHz- 400 kHz tartományban), és adja meg a frekvenciát és annak becsült pontosságát/hibáját. (Érdemes a mérést X-Y üzemmódban végezni, és keresni a p/2 fázistoláshoz tartozó pontot – miért ezt? Fejtse ki bővebben!)

alakot, ahol az fv(x) függvényt a c és alpha paraméterek szerint illesztjük az adat.dat állományból az 1. (x értékek) és a 2. (fv(x) értékek) oszlopához, úgy, hogy a 2. oszlop mérési pontossága/hibája a 3. oszlopban van megadva. Minden egyes illesztést nyomtasson ki, és csatolja a jegyzőkönyvhöz!

Adja meg mind a négy esetben a kapott (illesztett) c és a értékeket, hibájukkal együtt:

Mit tud mondani az a értékeiről és hibájáról?