|
|
1. ábra
A technika és a tudomány számos területén fordul elő az a probléma, hogy egy háromdimenziós tárgy belső szerkezetét kell megvizsgálni annak szétroncsolása nélkül. Ez megtehető példáu
l úgy, hogy a tárgyat átvilágítjuk olyan sugárzással, amelyet az nagyrészt átbocsát, azonban elegendő mértékben el is nyel ahhoz, hogy a belső szerkezet árnyképe kirajzolódjon. Talán legköznapibb példa ilyen mérésre az orvosi röntgen vizsgálat. Ha a vizsgálandó tárgy belső szerkezete közel kétdimenziós, illetve nem túl bonyolult, akkor ilyen árnyképfelvételek közvetlenül értelmezhetők. Bonyolultabb esetekben azonban néhány irányból készült felvétel nem elég ahhoz, hogy feltárja a belső szerkezetet. Ekkor használatosak a tomográfiás módszerek. A tomográfia görög elemekből alkotott szó, eredeti jelentése rétegfelvétel.
|
|
1. ábra
A fenti általános probléma, azaz egy háromdimenziós tárgy belső felépítésének visszállítása ké
tdimenziós árnyékképekből általában túl bonyolult, ezért a gyakorlatban tomográfiás rétegfelvételeket szokás készíteni. Ez azt jelenti, hogy a háromdimenziós tárgynak egy síkbeli metszetét vizsgájuk úgy, hogy a sík mentén különböző irányokból egydimenziós felvételeket készítünk és ezekből igyekszünk visszállítani a síkbeli szerkezetet. Természetesen a szerkezet itt az adott sugárzásra vonatkozó elnyelés térbeli változását jelenti. Tomográfián általában ennek a kétdimenziós problémának a megoldását értik.Az árnyképfelvételek feldolgozásával ekvivalens problémát jelent, ha egy tárgy saját sugárzásának eloszlását mérjük meg különböző irányokból és ebből akarjuk megkapni a kétdimenziós sugárzási intenzitáseloszlást. Ha a saját kibocsátott sugárzás el is nyelődik valamilyen mértékben a tárgyban, akkor a probléma bonyolultabbá válik. Ebben az esetben nem egy mennyiség (az abszorpció vagy az emisszió) eloszlását kell meghatározni, hanem egyszerre mindkettőt. A két alapesetet szemlélteti az 1. ábra.
Tomográfiás módszereket a plazmafizikától az anyagvizsgálaton keresztül az orvostudományig számos területen használnak, és a speciális alkalmazásokra ennek megfelelően számtalan módszert dolgoztak ki. Ebben a jegyzetben néhány megoldási elvet tekintünk át, és a laboratóriumi mérésben egy egyszerű módszerrel az alkalmazhatóság korlátait és sajátosságait vizsgáljuk meg. A vizsgálatot csak az emissziós tomográfia esetére korlátozzuk mivel az abszorpciós eset ezzel teljesen analóg. Míg a mérés az előbbi esetben a tárgy abszorpcióját, a második esetben annak emisszióját integrálja.
A 2. ábra az alapproblémát szemlélteti. Adott az x-y síkon az I(x,y) ú.n. forrás függvény amely a vizsgálandó objektum lokális sugárzási intenzitása az (x,y) pontban. Ennek egy ![]() szögben hajló, az origótól s távolságra haladó egyenes mentén vett integrálja az
szögben hajló, az origótól s távolságra haladó egyenes mentén vett integrálja az ![]() függvény. Rögzített
függvény. Rögzített ![]() esetén az
esetén az ![]() függvény az eredeti kétdimenziós forrásfüggvény egy vetülete. A tomográfiás probléma abban áll, hogy a vetületek ismeretében hogyan kapható meg a forrásfüggvény. A forrásfüggvény meghatározását a vetületekből visszaállításnak vagy inverziónak nevezzük. Természetesen egy valós mérés esetén az
függvény az eredeti kétdimenziós forrásfüggvény egy vetülete. A tomográfiás probléma abban áll, hogy a vetületek ismeretében hogyan kapható meg a forrásfüggvény. A forrásfüggvény meghatározását a vetületekből visszaállításnak vagy inverziónak nevezzük. Természetesen egy valós mérés esetén az ![]() függvényeket csak véges sok
függvényeket csak véges sok ![]() és s értéknél mérjük meg.
és s értéknél mérjük meg.
|
|
2. ábra A tomográfiai probléma. A sötétebb illetve világosabb területek a forrásfüggvény kisebb illetve nagyobb intenzitású területeit reprezentálják.
A fenti probléma általánosítását jelenti, ha a mért A imennyiségek az I(x,y) forrásfüggvénynek nem vetületei, hanem adott wi(x,y) súlyfüggvényekkel vett integráljai:
Ekkor a feladat a forrásfüggvény meghatározása ismert Ai és wi(x,y), ![]() esetén.
esetén.
Könnyen belátható, hogy véges számú vetületből tetszőleges forrásfüggvény nem állítható vi
ssza. Radon már 1917-ben megmutatta, hogy az összes szögeknél vett vetület ismeretében a forrásfüggvény egyértelműen előállítható. Természetesen a gyakorlati alkalmazásokban mindig véges számú vetület áll rendelkezésre, így tetszőleges forrásfüggvény nem állítható vissza.A jelenség nagyon hasonlít az analóg jelek digitalizálásánál felmerülő problémára. Ez utóbbi esetben is a mérendő jelet csak diszkrét időpontokban mérjük meg. Ahhoz, hogy ezekből a mi
ntákból az eredeti jel torzításmentesen visszaállítható legyen biztosítani kell, hogy a mintavételi frekvencia kétszeresénél magasabb Fourier komponensek ne legyenek a jelben (anti-aliasing filter).A tomográfia esetén hasonló a probléma. Gondoljunk például arra az egyszerű esetre, amikor két vetületet ismerünk egymáshoz képest 90 fokra (lásd a
3.ábrát), és a forrásfüggvény két csúcsból áll. Ebben az esetben nem tudjuk megmondani, hogy a két csúcs hogyan helyezkedik el, illetve négy csúcs esete sem zárható ki.|
|
3. ábra Egy egyszerű példa egyértelműen nem megoldható tomográfiai problémára. Két irányból mérve az a, b ,c forrásfüggvények ugyanazt a vetületet adják, így megkülönböztethetetlenek.
Ezen az egyszerű példán is látható, hogy véges számú mérés esetén a forrásfügg
vény csak a priori feltevések esetén állítható elő a a vetületekből. Sajnos a tomográfiás problémánál nem adható olyan egyszerű feltétel mint a digitális mintavételezésnél, már csak ezért sem mert az egyes gyakorlati alkalmazásokban a mérési geometria és a forrásfüggvény jellege is igen különböző lehet.|
|
4. ábra. Tomográfiás módszer zajérzékenysége két különböző forrásfüggvény esetén. Az a/ esetben a vetületből kiszámolt intenzitásfüggvény origóban felvett értéke sokkal érzékenyebb a mérési zajokra mint a b/ esetben.
A tomográfiás feladat másik súlyos problémája a megoldásra használt eljárások zajérzékenysége. Mivel a mérések mindig tartalmaznak valamennyi zajt is, ez elkerülhetetlenül az eredmény torzulását vonja maga után. Sajnos a zajérzékenység mértéke nem csak az alkalmazott visszaállítási eljárástól, hanem a forrásfüggvénytől is függ. Ezt szemlélteti a 4. ábra. Az a/ forrásfüggvény esetén az origót egy erősen sugárzó öv veszi körül, míg a b/ eloszlásnál a sugárzás folyamatosan növekszik az origóhoz közelítve. Ennek megfelelően a b/ esetben a forrásfüggvény egyenesek mentén vett integráljai mindig jelentős járulékot tartalmaznak az origóhoz legközelebb eső tartományból. Az a/ esetben ezzel szemben az integrál nagy része az erősen sugárzó gyűrűből származik. Ha a mérési zaj nagysága az integrál értékéhez képest mindkét esetben azonos, akkor az a/ esetben nyilván sokkal nagyobb az origó körüli sugárzáshoz képest, így ennek meghatározása sokkal pontatlanabb lesz.
Különböző alkalmazásokban igen eltérő számú
Ai mért érték állhat rendelkezésre. Gyorsan változó objektumok megfigyelésénél (például fúziós plazma röntgensugárzásának vizsgálatánál) nincs lehetőség arra, hogy kevés számú detektor mozgatásával mérjenek meg nagyszámú integrált. Ekkor minden egyes méréshez különálló detektor kell hogy tartozzon, így az integrálok száma legfeljebb néhány száz szokott lenni. Ezzel éppen ellentétes az orvosi vagy anyagvizsgálati tomográfia esete, ahol a statikusnak feltételezett objektumról kevés detektor mozgatásával akár százezer integrál is megmérhető. A nagyon eltérő számú bemenő adat miatt nyilvánvalóan a két tudományterületen alkalmazott tomográfiás módszerek is alapvetően különböznek.A tomográfiai probléma megoldására használatos módszereket két csoportra lehet bontani. Az analitikus típusú eljárásokban az I(x,y) forrásfüggvényt sorba fejtik egy teljes függvényrendszer fi(x,y) bázisfüggvényei szerint:
A sorfejtésből véges sok (m) tagot meghagyva a Pj együtthatókat határozzák meg a megoldásban. A cella vagy rács típúsú eljárásokban az x-y síkot valamilyen módon cellákra osztják. Az egyes cellákban állandónak tételezik fel az intenzitást, és ezeket az intenzitásértékeket számítják ki. Az első esetben jobban kihasználhatók a probléma szimmetriatulajdonságai, bár cella típusú módszerekben a cellák alakjának és méretének meghatározásával szintén figyelembe vehetők szimmetria megfontolások. Tulajdonképpen a cella típusú módszerek is tekinthetők analitikus módszereknek, amelyekben a sorfejtési függvényrendszer fi(x,y) függvénye 1 értéket vesz fel az i. cellában és 0-t máshol. Ennek megfelelően ebben a jegyzetben egységesen függvényrendszer szerinti sorfejtésként tárgyaljuk a tomográfiás probléma megoldását.
A cella módszerek olyan források esetén előnyösebbek, ahol az intenzitáseloszlás kisméretű m
aximumokat tartalmaz, míg az analitikus módszerek sima, lassan változó forrásfüggvények esetén jobbak. A felbontás növelésével mindkét megoldás ugyanahhoz az eredményhez konvergál, a kérdés csak az, hogy adott probléma megoldásához hány paramétert kell meghatározni.A fenti két csoport mellett elképzelhetők nemlineáris eljárások is, ahol a forrás néhány olyan paraméterét határozzuk meg, amelyek nem tekinthetők egy sorfejtés paramétereinek. Példa erre, ha egy az origó körül csúcsos eloszlás szélességét akarjuk meghatározni. Az ilyen eljárások nagyban különböznek az előző csoporttól és inkább a paraméter illesztésekre emlék
eztetnek, ezért ilyen módszert nem tárgyalunk ebben a jegyzetben.Feltéve hogy a forrásfüggvény egy a sugáron kívül nulla, tetszőleges ![]() irányban vett
irányban vett ![]() vetületből a radiális eloszlás visszaállítható az Abel-inverzió alkalmazásával,
vetületből a radiális eloszlás visszaállítható az Abel-inverzió alkalmazásával,
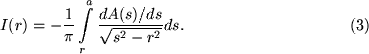
Itt tulajdonképpen arról van szó, hogy kívülről befelé haladva levonjuk az eloszlás sz
élének járulékát az egyes húrra vett integrálokból, ahogyan az az 5. ábrán látható.|
|
5. ábra Abel-inverzió elve. Ha a sugárzást állandónak tételezzük fel a számokkal jelölt gyűrűkben, akkor az 1. gyűrű sugárzása meghatározható A1-ből. Ezután A2-ből levonható az 1. gyűrű járuléka és a 2. gyűrű sugárzása megkapható, ...stb.
Mint az könnyen belátható, ebben a megoldásban a hibák halmozódnak. Gyakorlatban a vetületet csak véges sok helyen és hibával terhelten lehet meghatározni. A numerikus eljárás a mérési hibák miatt igen pontatlan lehet, ezért általában a mért vetületre valamilyen függvényt illesztenek és ezt analitikusan invertálják.
A nem hengerszimmetrikus eset vizsgálatához induljunk ki az (1) kifejezésből. Ebben a mért mennyiségek a forrásfüggvény tetszőleges, de ismert súlyfüggvényekkel vett integráljai. Helye
ttesítsük be a (2) kifejezés szerinti sorfejtést (1)-be. Az integrál és az összegzés felcserélésével azkifejezésre jutunk. Az Ai mért mennyiségeket és a Pj paramétereket egy-egy n illetve m dimenziós vektornak tekintve (4) felírható mátrix jelöléssel:
M egy ![]() dimenziós mátrix amely a paramétervektort a mérési vektorba transzformálja.
dimenziós mátrix amely a paramétervektort a mérési vektorba transzformálja.
A tomográfiás feladat megoldása ebben a megfogalmazásban egyszerűen az (5) lineáris egyenletrendszer megoldását jelenti. Elvileg ha n=m és az M mátrix determinánsa nem zéró akkor (5) egyértelműen megoldható. Ha n<m -- azaz kevesebb mérés van mint paraméter -- akkor a megoldás nem egyértelmű, ellenkező esetben nincs mindig megoldás. Az M mátrix függvénye mind a mérési elrendezésnek, mind a választott sorfejtésnek. Itt kell felhívni a figyelmet, hogy az alkalmazott véges sorfejtés automatikusan korlátozást jelent a kapható forrásfüggvényekre. Ha a valódi eloszlás nem jól közelíthető a választott sorfejtésben, akkor is kaphatunk megoldást ha a paraméterek számát a mérések száma fölé emeljük, de ez igen távol lehet a valódi forrásfüggvénytől.
Sajnos az M mátrix általában rosszul kondocoinált, azaz olyan, hogy a fenti direkt megoldás rendkívül érzékeny a zajra - így a gyakorlatban közvetlenül nem használható. A továbblépéshez rendezzük át az (5) egyenletet és emeljük négyzetre, így
Most ne követeljük meg a ![]() feltételt, hanem elégedjünk meg
feltételt, hanem elégedjünk meg ![]() minimumának meghatározásával. Ebben az esetben minden n és m esetén lesz megoldás.
minimumának meghatározásával. Ebben az esetben minden n és m esetén lesz megoldás.
Egy méréshez mindig tartozik valamilyen véges nagyságú mérési hiba is. Az illesztési probémákhoz hasonlóan azok a megoldások a legvalószínűbbek, amelyekre
ahol ![]() az egyes mérési csatornák mérési hibája. Ez a kifejezés egy m-1 dimenziós térfogatot jelöl ki a paramétertérben, melyben fekvő eloszlások mind megoldásai a tomográfia problémának. Ez a tartomány hosszan elnyúlik azokban az irányokban, amerre eső paraméterű eloszlások között a mérés kevés különbséget mutat ki. Sajnos, ilyen irányok általában előfordulnak a szokásos problémákhoz tartozó M mátrixok esetén. Ez a tulajdonság azt eredményezi, hogy a mérési zajok miatt a megoldás rendkívül zajérzékeny lesz.
az egyes mérési csatornák mérési hibája. Ez a kifejezés egy m-1 dimenziós térfogatot jelöl ki a paramétertérben, melyben fekvő eloszlások mind megoldásai a tomográfia problémának. Ez a tartomány hosszan elnyúlik azokban az irányokban, amerre eső paraméterű eloszlások között a mérés kevés különbséget mutat ki. Sajnos, ilyen irányok általában előfordulnak a szokásos problémákhoz tartozó M mátrixok esetén. Ez a tulajdonság azt eredményezi, hogy a mérési zajok miatt a megoldás rendkívül zajérzékeny lesz.
A zajérzékenység kiküszöbölésére kétféle megoldástípus használatos. Az első esetben a mérések
n számát jelentősen a paraméterek m száma fölé emelik. Ekkor a zajok hatása kiátlagolódik, ha az egyes mérési csatornák kellően függetlenek. Ha a mért értékekA másik eljárástípusnak az az elgondolása, hogy a zajok hatására olyan megoldások kaphatók, amelyeket a probléma ismeretében ki lehet zárni. Az ilyen megoldások kiküszöbölésére a méréseken kívül további infomációt visznek be a számításokba. Az egyik legelterjedtebb módszerben (maximum entrópia módszer) egy entrópia jellegű mennyiséget rendelnek az egyes forrásfüggvényekhez statisztikus fizikai analógia alapján. Ezután a ![]() függvénynek és az entrópiának egy súlyozott összegét minimalizálják. (Az entrópia súlya természetesen negatív). Ez az eljárás a (7) egyenlet által kijelölt paramétertartományból azokat a megoldásokat választja ki, amelyek infomációtartalma a legkisebb.
függvénynek és az entrópiának egy súlyozott összegét minimalizálják. (Az entrópia súlya természetesen negatív). Ez az eljárás a (7) egyenlet által kijelölt paramétertartományból azokat a megoldásokat választja ki, amelyek infomációtartalma a legkisebb.
A laboratóriumban a számítógépes tomográfia módszereit az emissziós tomográfia esetén lehet vizsgálni. A mérőeszköz vázlatát a
6. ábra mutatja.|
|
6. ábra A laboratóriumi mérőeszköz. Magyarázat a szövegben.
A vizsgálandó tárgy úgy jön létre, hogy egy diafilmet egy diavetítő segítségével kivetítünk egy fluoreszcens folyadékkal feltöltött üvegkádba. A kád feketére festett alumínium lemezekkel van körülvéve, amelyek árnyékolják a mérést a külső fényektől. A kád két oldalán egy 1 cm széles sávban nincs árnyékolás, ezek a csíkok szolgálnak a megfigyelésre. Az egyik
oldalon a mérőeszköz található, míg a másik oldalon vizuális megfigyelésre nyílik lehetőség.Ahol a vetített kép világos, ott a folyadék zöldes fluoreszcens fényben világít, melynek intenzitása arányos a gerjesztő fény intenzitásával és minden irányban egyforma intenzitással lép ki. Így egyszerű, térfogatában világító forrást kapunk. Természetesen a megvilágító fény egy kis része óhatatlanul szóródik a kád faláról és a mérést zavarja.
Fluoreszcens folyadékként a közismert Glycosept toroköblítő vizes oldatát használjuk 1, amely látható fénnyel történő megvilágítás hatására jól megfigyelhető zöld színben fluoreszkál.
A tárgy képének vetületét egy, a megfigyelő rés mentén mozgatható fototranzisztor detektálja. A tranzisztor előtt a fényt három apertúra kollimálja. A különböző irányú vetületek felvétele érdekében nem a detektor fordul el a tárgy körül, hanem a vetítő forog a filmmel együtt, így a fluoreszcens fényforrás forgása pótolja a detektáló rendszer körbeforgását.
Mind a detektor mozgása, mind a tárgy forgatása egy IBM PC kompatibilis számítógépről vez
érelhető. Ezt a feladatot egy kész, menürendszerrel vezérelhető program (GTOMO) látja el, a hallgatónak nem feladata a mérőrobot programozása.A fototranzisztoron a detektált fényintenzitással arányos áram folyik, amelyet erősítés és feszültséggé alakítás után a mozgás vezérlő IBM PC-ben található analóg-digitál konverter mér meg. A mérőprogram kijelzi az aktuálisan detektált fényintenzitást, illetve képes teljes eloszlások felvételére.
A tomográfiai probléma megoldása igen számításigényes feladat, ezért az IBM PC kompatibilis számítógép a mért integrálokat (vetületeket) a számítógéphálózaton keresztül továbbítja egy nagyobb teljesítményű workstation számítógépnek. Ez a kapott adatokból a mérőgépen beállított paraméterek mellet kiszámítja a forrásfüggvényt egy ekvidisztans kétdimenziós rácson (grid file) és az adatokat visszaküldi a mérést vezérlő PC-nek. Maga a mérőprogram meg tudja jeleníteni az eredményt színkódos ábra formájában. Háromdimenziós felület ábrát és szintvonalas ábrát a nyomtatás során lehet készíteni. A két számítógép összeköttetésének további részleteit a Függelék tartalmazza.
A kapott eredmények értelmezésénél figyelembe kell venni, hogy a vetítő
nem teljesen egyenletesen világítja ki a képet. Ez szemmel megfigyelve kevésbé látszik, mivel az emberi szem fényérzékelése nem lineáris azonban az eredményeknél az egyes területek intenzitásarányait módosíthatja.
A forrásfüggvény sorfejtésére a laboratóriumi gyakorlat során kétféle függvényrendszer, nevezetesen egy cella és egy analitikus módszer között lehet választani.
Ez első a mérőprogramban
grid módszernek nevezett rendszer a mérési tartományt egy négyzetráccsal fedi le. A rács felbontását, azaz az egy oldalán levő cellák számát változtatni lehet. A forrásfüggvény sorfejtésének paraméterei az egyes cellákban felvett értékek, ennek megfelelően a cellákban mindig állandó intenzitást tételez fel a program. Ebben az esetben a sorfejtés bázisfüggvényei egy-egy cellában 1 értéket vesznek fel, míg a többi cellában nullák. Egy példát mutat erre az esetre a 7. ábra.|
|
7. ábra A forrásfüggvény sorfejtésének egy bázisfüggvénye grid módszer esetén.
Nem szabad összekeverni a sorfejtésben alkalmazott rácsméretet az ábrázolásban (grid file) alkalmazottal. Míg az előbbi tetszőlegesen megválasztható paramétere a tomográfiai számolásnak, az utóbbi fix érték és csak az ábrázolásra jellemző.
A második fajta (Fourier) sorfejtés esetén a számítás polárkoordinátákban történik. Az origó körül egyenletes távolságokban köröket veszünk fel és az egyes körök között a forrásfüggvény szögfüggését Fourier sorba fejtjük. Az i. radiális intervallumban tehát az intenzitást
alakban fejezzük ki, n a Fourier sorfejtés rendje. A körök között a forrásfüggvényt a sugártól függetlennek tekintjük. A sorfejtési együtthatók a Pi0,Pi,jsés Pi,jc mennyiségek. Mind a körök száma, mind a Fourier sorfejtés rendje beállítható. k darab kör és n-ed rendű Fourier sorfejtés esetén a sorfejtési paraméterek teljes száma tehát k(2n+1). Egy bázisfüggvényt mutat a 8. ábra.
|
|
8. ábra A forrásfüggvény sorfejtésének egy bázisfüggvénye Fourier sorfejtés esetén. A kiemelkedő rész szélének fogazottsága a véges ábrázolási felbontás következménye.
Mint a 8. ábrán is látható, az intenzitás negatív értéket is felvehet. Ez a grid sorfejtés esetén csak akkor lehetséges, ha a paraméterek negatív értéket vesznek fel, így a tomográfia mérőprogram lehetővé teszi ebben a sorfejtésben a paraméterek értékének korlátozását pozitív számokra. A Fourier sorfejtés esetén ilyen feltételt nem lehet alkalmazni. Az adott problémában a negatív intenzitásértékeknek nincs fizikai értelmük.
A sorfejtési együtthatókat a tomográfia program a (6) képlet szerinti ![]() kifejezés numerikus minimalizálásával határozza meg. Kezdeti feltételként minden paramétert nulla értékre állít, majd innen kiindulva keresi a
kifejezés numerikus minimalizálásával határozza meg. Kezdeti feltételként minden paramétert nulla értékre állít, majd innen kiindulva keresi a ![]() függvény minimumát. Ez a kezdeti érték befolyásolja az eredményt ha a tomográfiás probléma megoldása nem egyértelmű. A sorfejtési paraméterértékek nem kaphatók meg a programból, hanem az eredmény a forrásfüggvény ábrázolása egy fix felbontású négyzetrácson (GRID file).
függvény minimumát. Ez a kezdeti érték befolyásolja az eredményt ha a tomográfiás probléma megoldása nem egyértelmű. A sorfejtési paraméterértékek nem kaphatók meg a programból, hanem az eredmény a forrásfüggvény ábrázolása egy fix felbontású négyzetrácson (GRID file).
A tomográfia program nem tartalmaz a mérésen kívül további információt, így megfelelő ere
dményt a sorfejtésnek és a mérési felbontásnak a helyes megválasztásával lehet kapni. Ez azt sugallja, hogy a mindig a maximális felbontással kell mérni. Ez az út természetesen nem járható, mivel a mérési idő korlátozott, és a számítási idő is jelentősen függ az alkalmazott felbontástól. A mérések egy részében a mérési feladat része az, hogy a tomografálandó ábra előzetes szemrevételezésevel meghatározzuk az alkalmazandó sorfejtés típust, felbontást valamint a mérésben a vetületek és az egy vetületben megmért pontok számát.A tomográfiás laborgyakorlat során szükséges kétdimenziós I(x,y) függvények ábrázolása áttekinthető formában. Az alábbiakban ennek néhány gyakran használt módozatát foglaljuk össze.
Mindkét program a függvényt egy ú.n. grid formában kapja meg. Ez a függvény értékeket írja le egy ekvidisztans négyzetrács pontjaiban. A tomográfia mérő és feldolgozó program ilyen GRID file-okat készít.
|
|
9. ábra Egy adott irányból ábrázolt 3D függvény.
Kétdimenziós függvény ábrázolható mint egy háromdimenziós felület (3D surface). Ekkor a függvény értéket az (x,y) pontban a felület helyi z magassága szemlélteti. A felületet képét egy tetszőlegesen megválasztható irányból mutathatjuk be, ahogyan az a 9. ábrán látható.
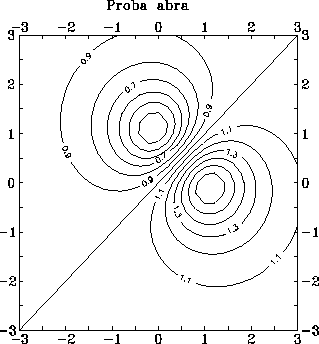 |
10. ábra Szintvonalasan ábrázolt függvény.
Egy 3 dimenziós felületet kétdimenziós felületet szintvonalas ábra (contour plot) formájában is ábrázolhatjuk. Ekkor az ábrázolás síkban történik, a program a felület azonos értékekhez tartozó szintvonalainak helyzetét számolja ki és rajzolja, ahogyan az például a 10. ábrán látható.
Ennek az ábratípusnak előnye a háromdimenziós felület ábrával szemben, hogy pontosan leo
lvasható egyes struktúrák helyzete és alakja, viszont az ábra mint egész nehezebben tekinthető át, például nehezen különböztethetők meg a minimumok és a maximumok.Egy harmadik ábrázolási mód a színkódos (mesterséges színes) ábrázolás. Ekkor a (x,y) pontban a függvény amplitúdóját az oda rajzolt pont színe reprezentálja. Az ábra értelmezéséhez egy színskála tartozik, amely lehet színes vagy egy egyszerű szürke skála. Ez a fajta ábra hasonlít a szintvonalas ábrázoláshoz, és gyakran kombinálják is azzal. A tomográfia laborgyakorlaton az IBM PC-n futó mérőprogram képes a képernyőn színkódos ábrát készíteni, azonban jelenleg ezt színesben kinyomtatni nem lehet. Szürke színskálás ábra készítésére a workstation számítógép képes.
Egyes esetekben célszerű mind háromdimenziós mind szintvonalas ábrát készíteni a függvén
yről.Feladatok
1. Előkészület a mérésre.
Ismerkedjen meg a laboratóriumi mérőeszközzel! Keresse meg a jegyzet leírása és ábrája alapján a berendezés részeit. Keresse meg a fénydetektort és kapcsolja be az elektronikát. Ezt a tápf
eszültséget adó elemek közelében található kis dugó aljzatba dugásával lehet megtenni. A detektor a bekapcsolás után körülbelül tíz perccel használható mérésre, ennyi idő kell a stabil nulla szint beállásához. Kapcsolja be a mérés vezérlő számítógépet! A vetítőnek még nem kell világítania, azt a számítógép csak a mérés idejére kapcsolja be.
Vegye ki az üvegkádat, amely a vetítőt és az árnyékolást tartó torony leemelésével érhető el. Töltse fel a jelig csapvízzel és csepegtessen a vízbe 80 csepp Glycosept olda
tot. Keverje a folyadékot, amíg a színe egyenletes nem lesz. Várjon néhány percet míg a folyadék megnyugszik, ez alatt kapcsolja be mozgásvezérlő eletronikát. Ennek kapcsolója az alsó doboz hátoldalán található. A bekapcsolás után amennyiben a vezérlő doboz elején a piros hibajelző LED kigyullad, azt a CLEAR feliratú gomb megnyomásával törölni kell. Adja ki a számítógépen a WSTEST parancsot, amely megszólítja a tomográfiai számításokat végző Silicon Graphics Workstationt és megvizsgálja, hogy működik-e a számítógéphálózat a két számítógép között.
A keverőpálcával kaparja le az üvegkád belső felületéről, különösen a megfigyelő ablakról az esetleg rárakódott levegőbuborékokat. Ez a lépés azért szükséges, mert a megmaradó buborékok a fényt szórják és a mérést meghamisíthatják. Győződjön meg arról, hogy a fénydetektor megf
elelő magasságban áll-e úgy, hogy éppen a hátsó megfigyelő rés közepén van. Ezután helyezze a kádat a helyére a jelölt oldalával előre és helyezze fölé a mérőszerkezetet. Figyeljen arra, hogy a szerkezet a jelölt helyre kerüljön és hátsó fala párhuzamos legyen a mozgatószerkezet mozgásirányával. Ezután helyezze el a tornyot úgy, hogy a detektor a megfigyelő résben legyen, de az üvegkádhoz ne érjen sehol hozzá. A detektor kollimáló csövén található árnyékoló szivacsot húzza a rés elé, hogy csökkentse az ott beszűrődő fényt.
Indítsa el a mérés vezérlő IBM PC számítógépen a GTOMO programot! Először a kézi állítás menü jelentkezik be, ahol a detektor nulla pozícióját kell beállítania: a kád tartójá
n található jelölést és a detektor közepét hozza egyvonalba, a vetítőt pedig állítsa nyugalmi helyzetbe (ekkor ki- és beteheti a diákat). Ezek után kapcsolja ki a vetítő lámpáját, és lépjen ki a kézi léptetés menüből, valamint a programból. A program az induláskori detektorpozíciót tekinti null pozíciónak. A tomográfiás mérés mindig e körül szimmetrikusan zajlik. Ha a fenti lépéseket elvégezte, a berendezés készen áll a mérésre.
Keresse meg az 1. számú diapozitívot, amelyen egy fémlemezbe fúrt kis lyuk látható és a jelölésnek megfelelően helyezze a vetítőbe.Lépjen be újból a GTOMO programba, és most már ügyeljen arra, hogy a mérés közben ne lépjen ki a GTOMO programból, mert ekkor az újraindításkor esetleg ismét be kell állítania a null pozíciót. Ha más programot akar indítani, vagy DOS parancsot akar kiadni, akkor használja a DOS Shell menüpontot.
Kapcsolja be a vetítőt az induló menüben és a vetítő forgatásával (phi irány) az eredetire meről
eges irányból ellenőrizze, hogy a fénypont közelítőleg ugyanazon a helyen marad-e.
Dokumentálja a mérőeszköz beállítását avval, hogy a felveszi a fénypont egy vetületét a Measure menu Single Measure pontja segítségével. A mérés felbontását (tehát a mérések számát egy v
etületben) a Set parameter menuben lehet beállítani úgy hogy a két mérés közötti lépés nagyságot kell megadni. A program mindig -150-től +150 lépésig mér. A felbontást úgy válassza meg, hogy a fényfolt jól látszódjon. Írja a mérés eredményét egy file-ba a File menü Save single scan pontja segítségével. Nyomtassa ki a File->Print Single Scan menüponttal. A kinyomtatott képet csatolja a jegyzőkönyvhöz!2. Egy pont tomografálása
Állítsa be az vetületben felvett pontok számát körülbelül 20-ra Végezzen egy tomográfiás mérést két irányból evvel a felbontással. Állítsa a tomográfiás módszert grid típusúra a rács méretét pedig 10-re és a paraméterértékeket ne korlátozza pozitívra. Tomografálja a mérési eredményt ezekkel a paraméterekkel. A parmétereket adja meg itt:
Ábrázolja és nyomtassa ki az eredményt a File->Print Tomographed Results menüponttal FIGYELEM! A program csak a legutoljára tomografált képet tudja helyesen kinyomtatni!. A kinyomtatott képet sorszámozza (ezt rögzítse itt) és csatolja a jegyzőkönyvhöz!
Figyelje meg, hogy visszaadja-e a számolás a tényleges intenzitáseloszlást. Vajon a kapott intenzitáseloszlás vetületei kielégítik-e a mérést? Magyarázza meg, hogy mit tapasztal:
Az adott mérésből lehet-e olyan módszerrel tomografálni amely jobban visszaadja az igazi forrásfüggvényt? Ha talál ilyen tomográfiai beállítást, akkor adja meg ezeket a paramétereket, az eredmény pedig ábrázolja és magyarázza meg mi okozza a különbséget (a kinyomtatott képet csatolja a jegyzőkönyvhöz!).
Növelje meg a mérések számát úgy, hogy körülbelül megegyezzen a sorfejtési paraméterek számával (100). Ezt kétféleképpen is tegye meg. Először úgy, hogy két vetületet vesz fel, de az összes mérési pontok száma körülbelül megegyezik a sorfejtés paramétereinek számával. A paraméterek értékét adja meg itt, a kinyomtatott képet pedig (sorszámozva) csatolja.
Másodszor növelje meg a vetületek számát, de az egy vetületben levő mérések számát hagyja változatlanul. A paraméterek értékét adja meg itt, a kinyomtatott képet pedig (sorszámozva) csatolja.
Mi lett az eredmény? Miért van különbség a két eset között?
3. Két pont tomografálása
Tegye a vetítőbe a 2. számú képet, amelyen 2
lyuk látható. Végezzen egy mérést két irányból és tomografálja az eredményt 10x10110-es grid módszerrel, csak pozitív paramétereket megengedve. A paraméterek értékét adja meg itt, a kinyomtatott képet pedig (sorszámozva) csatolja. Magyarázza meg az eredményt!Végezzen olyan (alább dokumentált) mérést, amelyik a mért értékek lehető legkisebb száma esetén már egyértelmű eredményt ad!
4. Cella és Fourier módszer összehasonlítása
Tegye a vetítőbe a 3. számú képet, amelyen egy nagyméretű kerek folt látható. Végezzen olyan méréseket, amellyel a grid illetve a Fourier tomográfiás módszerrel a lehető legkevesebb méré
ssel és paraméterszámmal visszakapja a kép alakját. Jegyezze fel a mérésekhez és a tomografáláshoz szükséges időt, a mért mennyiségek számát, a számolásban használt paraméterek számát és a számítás idejét. A kinyomtatott képeket (sorszámozva) csatolja (megjegyzés: a program Fourier tomográfiás képet nem, csak grid eljárással készült képet tud nyomtatni, ezért a képernyőn hasonlítsa össze a Fourier eljárással kapott képet a grid eljárással kapott ábrákkal!). Mit tapasztal? Hogyan változik a rekonstrukció minősége a parméterek változtatásával?5. Bonyolultabb ábrák feldolgozása
A laborgyakorlat hátralevő idejében mérjen meg és dolgozzon fel a laborvezető által adott k
ülönböző ábrákat. Próbálja optimálisan megválasztani a mérések számát, a tomográfiás módszert és a felbontást. Mérje meg és jegyezze fel mindig a mérési és számolási időt, a mérések és a paraméterek számát. Nyomtassa ki a kapott eloszlásokat.