next up previous
Következő: Lineáris feszültség-idő függvények előállítása | Tartalomjegyzék | Előző: Emittercsatolt multivibrátorok

Emittercsatolású bistabil multivibrátor (Schmitt-kör)

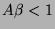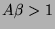Az 5.6.11. ábrán látható emittercsatolású bistabil multivibrátor egy hosszúfarkú-párból és egy galvanikus pozitív visszacsatolásból áll. A bemenőjel és kimenőjel közötti összefüggést az 5.6.12. ábrán ábrázoltuk különböző visszacsatolási tényezők mellett. Ha $A\beta <1$, akkor az áramkör lineáris erősítőként működik. A visszacsatolás növelése az erősítés értékét növeli, majd ha $A\beta =1$, akkor a vezérlési tartomány zérusra csökken: az áramkörnek a bemenő feszültségtől függően két kimeneti állapota lesz. Az áramkör tehát amplitudó érzékeny billenőkörré vált. Ha $A\beta>1$, akkor az oda- illetve visszabillenési feszültségek nem fognak tovább megegyezni: az áramkörnek ún. hiszterézise lesz.


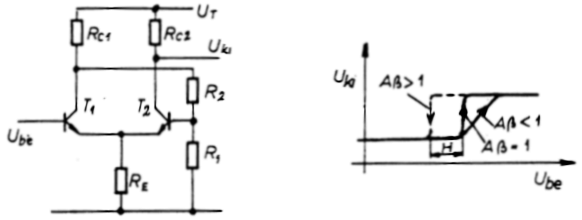
5.6.11/12. ábra


Az 5.6.13. ábra alapján megvizsgáljuk, hogy az áramkör egy adott bemenőjelre milyen kimenőjellel válaszol. Bemenőjelként egy lineárisan fel- és lefutó feszültség-hullámalakot választottunk. Amíg a bemenőjel nem éri el az első billenési szint értékét, addig a T2 tranzisztor vezet, T1 le van zárva. Változás akkor következik be, ha T2 bázisfeszültsége megközelíti a T1 által megszabott közös emitterfeszültséget, vagyis (feltéve, hogy T2 bázisa az R1-R2 osztót nem terheli):

\begin{displaymath}U_{B1} \simeq U_T {R_1\over R_1+R_2+R_{C1}}.\end{displaymath}

Ha a bemeneti feszültség ezt az értéket meghaladja, akkor az áramkör átbillen, (T1 vezet, T2 lezárt) és ebben az átbillent állapotban marad, míg a bemenőjel a második billentési szint értékére nem csökken.


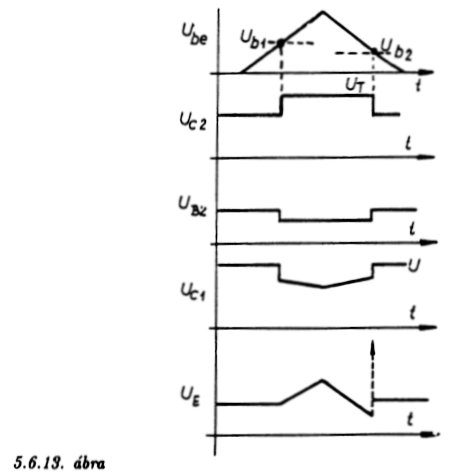
5.6.13. ábra


Az átbillent állapotban T1 emitterkövetőként működik; a visszabillenés felétele az, hogy a két tranzisztor bázisfeszültségei egyezzenek meg, vagyis

\begin{displaymath}U_{B2} = \left( U_T - {U_{B2}\over R_E}R_{C1}\right){R_1\over R_1 + R_2}\end{displaymath}

(felhasználtuk azt is, hogy a visszacsatoló áramkör nem terheli T1 kollektorát). A két billenési szint különbsége a már említett hiszterézis. A Schmitt-kör nagyon fontos, igen sokszor alkalmazott áramkör, többek között különböző amplitudójú jelek amplitudó uniformizálására használható (l. 5.6.14. ábra). Érdekes alkalmazási lehetőséget mutat az 5.6.15. ábra is. Ez az áramköri elrendezés lehetővé teszi nagyon rövid időtartamú impulzusok amplitudójának mérését. Az áramkör kimenetét figyelve ugyanis megállapítható, hogy a bejövő impulzus amplitudója (ui ) és az előfeszültség (UE ) összege elérte-e az első billenési szint (UB1 ) értékét. Vagyis kimenőjelet akkor kapunk, ha

\begin{displaymath}u_i + U_E \ge U_{B1}.\end{displaymath}

Ez az áramkör különös fontosságú az impulzus-amplitudó mérésen alapuló nukleáris jelspektrometriában.


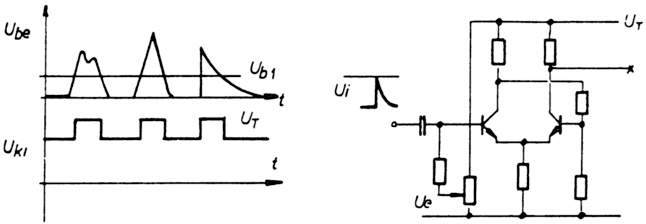
5.6.14/15. ábra
next up previous
Következő: Lineáris feszültség-idő függvények előállítása | Tartalomjegyzék | Előző: Emittercsatolt multivibrátorok

1999-09-23