Lineáris feszültség-idõ függvények elõállítása

5.7.1/2. ábra

Már megvizsgáltuk, hogy egy telepbõl, ellenállásból és kondenzátorból álló áramkörben a kondenzátorban kialakuló feszültség nemlineárisan növekszik, mert a kondenzátor feltöltõdésével a töltõáram csökken. Ha azonban az 5.7.2. ábra szerint az áramkörbe egy segédfeszültséget helyezünk, mely minden idõpillanatban akkora értékû, hogy az áramkörben folyó áram állandó tud maradni, a kondenzátor feszültsége lineárisan növekszik.

5.7.3. ábra

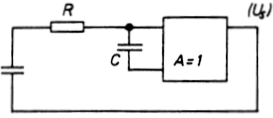
Ennek feltétele az, hogy a beiktatott segédfeszültség értéke pontosan egyezzék meg a kondenzátor feszültségével. Ezt a segédfeszültséget egy zérus kimenõ ellenállásúnak feltételezett vezérelt erõsítõ szolgáltathatja. Az 5.7.3. ábra szerinti megoldásban a kondenzátor feszültségét pontosan lemásoljuk, és ezt a feszültséget hozzáadjuk a kondenzátor töltésért felelõs hálózathoz. A töltõáram akkor lesz állandó, ha az erõsítés pontosan egységnyi. 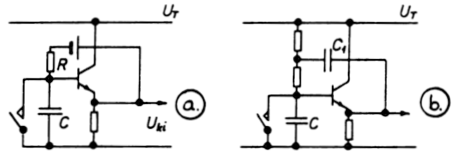A fenti elvek alapján szerkesztett áramkör, az ún. utánhúzó (boot-strap) kapcsolás vázlatát az 5.7.4. ábra tünteti fel. Az "a" ábrán az áramkör elvi felépítése látható. A kondenzátor feszültségét egy emitterkövetõ másolja le, ennek kimenete csatlakozik a telephez. Az áramkör a kapcsoló kinyitására indul, kimenetén lineárisan növekvõ feszültséget kapunk. A "lebegõ potenciálú" telep azonban kellemetlen, helyettesítésére a "b" ábra szerinti változatában a feszültségforrás szerepét a C₁ (jó nagy) kondenzátor veszi át.

5.7.4. ábra

Meg kell jegyeznünk, hogy a Miller effektus is jól használható lineárisan változó jelek elõállítására. Itt ugyanis a kapacitást "sokszorozzuk meg", amivel az idõállandót növeljük. Ha pedig a beiktatott erõsítõ a kialakuló exponenciális görbe kezdeti, majdnem lineáris szakaszát erõsíti, igen jóminõségû kimenõjelhez juthatunk.