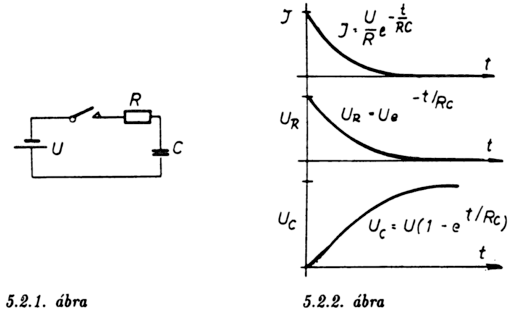
Tekintve, hogy az exponenciális görbe igen gyakran előfordul a
későbbiekben, a 5.2.3. ábrán részletesen is kirajzoltuk.
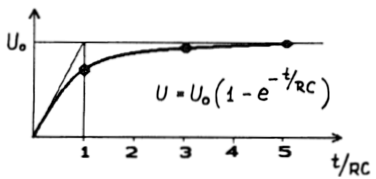
(Exponenciális görbét tehát az alábbiak szerint rajzolunk:
-- berajzoljuk a görbe kezdőpontját;
-- berajzoljuk azt a vízszintes egyenest, ahová a görbe tartani fog;
-- a t/RC = 0 értéknél berajzoljuk a görbe kezdeti iránytangensét;
-- a t/RC = 1 értéknél a függőleges távolságot kb. 1:2 arányban osztjuk;
-- a t/RC = 3 értéknél a végértéket 5 százaléknyira megközelítjük;
-- a t/RC = 5 értéknél a hiba már csak néhány ezreléknyi, kissé erőszakos
megfogalmazás szerint itt fejeződik be a görbe.)
A továbbiak során számos bonyolultabb bekapcsolási jelenséget is
erre az egyszerű esetre fogunk visszavezetni. A kialakuló exponenciális
jelalakokat olymódon szerkesztjük meg, hogy berajzoljuk a bekapcsolás
előtti és bekapcsolás után hosszú idő múlva elért szinteket, majd a
kettő közötti átmenetet exponenciális függvényként ábrázoljuk. Az
exponenciális görbét jellemző időállandót az áramkör felépítéséből úgy
állapíthatjuk meg, hogy pl. a kondenzátor két sarka felől "belenézünk
az áramkörbe" és az így látható áramköri ellenállást határozzuk meg,
ezen ellenállásnak és a kondenzátornak a szorzata adja az időállandót.
Ez az eljárás természetszerűleg csak akkor követhető, ha a tranziens
folyamatot egyetlen exponenciális időfüggvény írja le (pl. az
áramkörben sok ellenállás, de csak egyetlen kondenzátor van).