Következõ Boole függvények kanonikus alakja | Tartalomjegyzék | Elõzõ Bool algebra,bevezetés

Boole algebra

A Boole algebra (eredete 1854-ben) logikai összefüggések tanulmányozására alkalmas szimbólikus módszer. Természetszerûleg alkalmas más, két állapottal rendelkezõ rendszerek vizsgálatához is. Mi a Boole algebrát matematikai hátterétõl és kapcsolataitól elvonatkoztatva olyan eszköznek tekintjük, mely lehetõvé teszi az ÉS, VAGY, inverter áramkörök közötti mûködési kapcsolatok formai leírását. (A továbbiakban ennek megfelelõen a VAGY kapcsolatot + jellel, az ÉS kapcsolatot 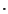$\cdot$ jellel jelöljük.) A Boole algebra alaptételeinek most következõ felsõrolásánál tehát "igazolás"-ként nem a matematikára, hanem az áramkörök mûködésére utalunk. A Boole algebra alapvetõ összefüggései: 1. Az 1 érték valamely definiált feszültségérték (pl. 3.5V) meglétét jelzi. A 0 érték az elõbb definiált feszültségérték nemlétét jelzi (pl. 0 V).

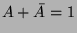$A+\bar{A} = 1$

Külön fel kell hívni a figyelmet a 4. pontban található ún. De Morgan szabályokra, melyek egészen általánosan is igazak abban a formában, hogy egy logikai függvény inverzét (kiegészítõjét) úgy kapjuk meg, hogy minden + jelet 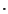$\cdot$ jellel és minden betût (vagy betûcsoportot) a kiegészítõjelével (komplementerével) kell helyettesíteni. A fenti szabályok célszerû alkalmazhatóságára két egyszerû példát vizsgálunk. 1. Egyszerûsítendõ a következõ kifejezés:

$\begin{displaymath}f=(A+C)\cdot (A+D)\cdot (B+C) \cdot (B+D)\end{displaymath}$

A 8/5 összefüggés ismételt alkalmazásával:

$\begin{displaymath}f=(A+C\cdot D)\cdot (B+C\cdot D)= A\cdot B + C\cdot D\end{displaymath}$

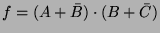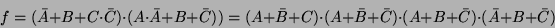A 6.1.1. ábrán felrajzoltuk az eredeti f függvényt, valamint a vele ekvivalens egyszerûsített függvényt realizáló hálózatot. Jól láthatóan az eredeti hálózathoz $4\times 2 + 4 = 12$ diódára volt szükség. A diódák száma egyszerûsítés után $2\times 2 + 2 = 6$ -ra csökkent.

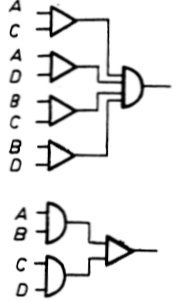
6.1.1. ábra

2. Bovítsük az 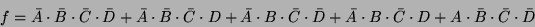$f = (A+\bar{B})\cdot (B+\bar{C})$ függvényt úgy, hogy az felírható legyen olyan összegtényezõk szorzataként, amely összegtényezõk mindegyike tartalmazza mindhárom bemeneti változót. Egy lehetséges megoldás:

$\begin{displaymath}f= (\bar{A}+B+C\cdot \bar{C})\cdot (A\cdot \bar{A}+B+\bar{C})... ...(A+\bar{B}+\bar{C})\cdot(A+B+\bar{C})\cdot(\bar{A}+B+\bar{C}) \end{displaymath}$

Következõ Boole függvények kanonikus alakja | Tartalomjegyzék | Elõzõ Bool algebra, bevezetés

1999-09-23