next up previous
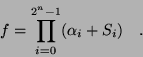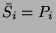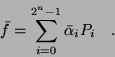
Következő: Kétváltozoás Bool függvények | Tartalomjegyzék | Előző: Boole algebra

Boole függvények kanonikus alakja

A Boole függvények mindig felírhatók kanonikus alakban, vagyis összegtényezők szorzataként, vagy szorzattényezők összegeként. A szorzattényezők a logikai változók logikai szorzatai (az összes változó szerepel minden tényezőben). Természetesen a változó helyett annak negáltja is előfordulhat. Az összegtényezők a logikai változók logikai öszegeként állíthatók elő. A fenti megállapítás igazolására lássunk egy egyszerű példát. Tervezzünk logikai hálózatot, melynek kimenete 0, ha C jelen van, vagy D-vel vagy B-vel egyidejűleg A is jelen van. A feladat ABCD logikai változókhoz tartozó igazságtáblázata a következő:


truecm
A B C D f
0 0 0 0 1
0 0 0 1 1
0 0 1 0 0
0 0 1 1 0
0 1 0 0 1
0 1 0 1 1
0 1 1 0 0
0 1 1 1 0
1 0 0 0 1
1 0 0 1 0
1 0 1 0 0
1 0 1 1 0
1 1 0 0 0
1 1 0 1 0
1 1 1 0 0
1 1 1 1 0
A keresett logikai függvényt egyszerűen felírhatjuk:

\begin{displaymath}f=\bar{A}\cdot \bar{B}\cdot \bar{C}\cdot \bar{D}+\bar{A}\cdot... ...\cdot \bar{C}\cdot D+A\cdot \bar{B}\cdot \bar{C}\cdot \bar{D} \end{displaymath}

mert f nyilván akkor lesz 1 értéku, ha bármely szorzattényező az 1 értéket veszi fel. Ugyanezt a függvényt azonban másként is előállíthatjuk:

\begin{displaymath}f=(A+B+\bar{C}+D)\cdot (A+B+\bar{C}+\bar{D})\cdot (A+\bar{B}+\bar{C}+D)\cdot (A+\bar{B}+\bar{C}+\bar{D})\cdot \end{displaymath}


\begin{displaymath}\cdot (\bar{A}+B+C+\bar{D})\cdot (\bar{A}+B+\bar{C}+D)\cdot (\bar{A}+B+\bar{C}+\bar{D})\cdot (\bar{A}+\bar{B}+C+D)\cdot \end{displaymath}


\begin{displaymath}\cdot (\bar{A}+\bar{B}+C+\bar{D})\cdot (\bar{A}+\bar{B}+\bar{C}+D)\cdot (\bar{A}+\bar{B}+\bar{C}+\bar{D})\end{displaymath}

A felírás nyilván helyes, mert a szorzat bármely tagjának 0 értéke esetén az egész függvény értéke 0 lesz. Az előző folyamat általánosításához a szorzattényezőket P (Product), az összegtényezőket S (Sum) tényezőknek fogjuk elnevezni. Az egyes tényezőket olyan index-szel látjuk el, mely egyértelműen utal az igazságtáblázat megfelelő sorára, vagyis pl.

\begin{displaymath}\bar{A}\cdot \bar{B}\cdot \bar{C}\cdot \bar{D} = P_0\quad, \end{displaymath}


\begin{displaymath}\bar{A}\cdot \bar{B}\cdot \bar{C}\cdot {D} = P_1\quad, \end{displaymath}


\begin{displaymath}\bar{A}+ \bar{B}+ \bar{C} + \bar{D} = S_{15}\quad. \end{displaymath}

Ezen tényezők felhasználásával tehát minden n változós Boole függvény felírható

\begin{displaymath}f=\sum _{i=0}^{2^n-1} \alpha _i P_i\end{displaymath}

formában, ahol 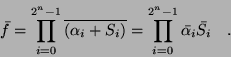$\alpha _i$ az igazságtáblázat f oszlopának megfelelő érték (karakterisztikus szám). A függvény tehát annyi tényezőt fog tartalmazni, amennyi az f oszlopban található 1-ek száma. Nyilvánvaló, hogy f másként is felírható:

\begin{displaymath}f=\prod \limits _{i=0}^{2^n-1} (\alpha _i + S_i) \quad .\end{displaymath}

Ezekben a felírási formákban tehát annyi összegtényező fog szerepelni, mint ahány 0 szerepel az igazságtáblázat f oszlopában. Az f függvények ilyen formában történő megadását kanonikus alaknak nevezzük. Érdemes felfigyelni arra, hogy a kanonikus alak egyszerű lehetőséget biztosít a kiegészítőképzésre is:

\begin{displaymath}\bar{f} = \prod \limits _{i=0}^{2^n-1} \overline{(\alpha _i +... ...prod \limits _{i=0}^{2^n-1} \bar{\alpha _i} \bar{S_i}\quad .\end{displaymath}

Mivel azonban $\bar{S}_i = P_i$,

\begin{displaymath}\bar{f}=\sum _{i=0} ^{2^n-1} \bar{\alpha}_i P_i\quad .\end{displaymath}

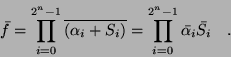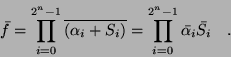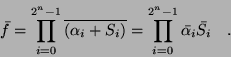Összefoglalva tehát egy kanonikus alakban megadott Boole függvény kiegészítőjét az adott függvény $\alpha _i$ karakterisztikus számainak kiegészítő értékei határozzák meg. Ha az f kiegészítő függvény kanonikus P alakban adott, akkor csak azok a P tényezők jelennek meg, amelyeknek $\alpha _i$-je eredetileg 0 volt, ha f kanonikus S alakban adott, akkor csak azok az S tényezők jelennek meg, amelyeknek $\alpha _i$ -je eredetileg 1 volt. Boole függvények természetesen nemcsak kanonikus alakban írhatók fel, az előző fejezet példái ezt egyértelműen mutatják. A 2. példa azonban arra is utal, hogy nem kanonikus formában adott Boole függvény is mindig kanonikus alakra hozható. A kanonikus alak használatának kifejezett előnyei vannak az áramkörök tervezésében. Az e szerint realizált hálózatokban ugyanis minden bemeneti jel két kapuáramkörön keresztül jut a kimenetre. Ha az áramkörökön való jeláthaladási sebesség véges, akkor ugyanis veszélyes olyan rendszert használni, ahol a kimenet nem mindig egyértelműen determinált.
next up previous
Következő: Kétváltozoás Bool függvények | Tartalomjegyzék | Előző: Boole algebra


1999-09-23