Következõ: Boole függvények minimalizálása | Tartalomjegyzék | Elõzõ: Tartalomjegyzék

Kétváltozós Boole függvények

A kétváltozós Boole függvények általánosan felírhatók az alábbi alakban:

$\begin{displaymath}f(A,B)=\alpha_0P_0+\alpha_1P_1+\alpha_2P_2+\alpha_3P_3\quad .\end{displaymath}$

A kétváltozós Boole függvények igazságtáblázatát, valamint a karakterisztikus számok lehetséges értékét az 6.3.1. táblázat tartalmazza. A függvények mellett feltüntettük az egyetlen áramköri egységként leggyakrabban realizált kétváltozós függvények közhasználatú neveit. Az ÉSNEM (NAND), a VAGYNEM (NOR) valamint a KI(záró)VAGY (XOR - eXclusive OR) ármkörök igen fontosak, mivel szerepük a digitális gépek tervezésében kiemelkedõ. A NAND és NOR áramkörök logikai funkciója könnyen átlátható, a XOR kisebb magyarázatot igényel.

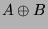0 $A\cdot B$ $A\cdot \bar{B}$ A $\bar{A}\cdot B$ B $A\oplus B$ A+B

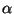A B $\alpha$ 0 1 2 3 4 5 6 7

0 0 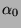$\alpha_0$ 0 0 0 0 0 0 0 0

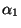0 1 $\alpha_1$ 0 0 0 0 1 1 1 1

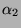1 0 $\alpha_2$ 0 0 1 1 0 0 1 1

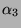1 1 $\alpha_3$ 0 1 0 1 0 1 0 1

AND XOR OR

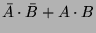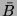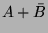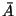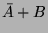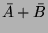$\bar{A}\cdot \bar{B}$ $\bar{A}\cdot \bar{B}+A\cdot B$ $\bar{B}$ $A+\bar{B}$ $\bar{A}$ $\bar{A}+B$ $\bar{A}+\bar{B}$ 1

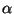A B $\alpha$ 8 9 10 11 12 13 14 15

0 0 $\alpha_0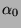$ 1 1 1 1 1 1 1 1

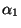0 1 $\alpha_1$ 0 0 0 0 1 1 1 1

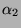1 0 $\alpha_2$ 0 0 1 1 0 0 1 1

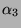1 1 $\alpha_3$ 0 1 0 1 0 1 0 1

NOR KOINC. NAND

6.3.1. táblázat

A XOR mûvelet definíciója:

$\begin{displaymath}A \oplus B = \bar{A}\cdot B + A \cdot \bar{B}\quad.\end{displaymath}$

A XOR áramkör lényegében bináris számok bináris összeadásra szolgál, mivel a 0 + 1 = 1 összefüggésen túlmenõen az 1 + 1 = 0 feltételt is teljesíti (ilyenkor természetesen átvitel is keletkezik, amivel tényleges összeadóknál külön kell foglalkozni). Bináris számok egy helyiértékének az összeadásához a XOR áramkörbõl kettõre van szükség, hogy az összeadandó számok, valamint az elõzõ helyiérték átvitelbitjét egyaránt figyelembe tudjuk venni. A XOR áramkört szívesen nevezik - éppen ezért - fél-összeadónak is. A XOR komplementer áramköre a KOINCIDENCIA. Itt meg kell jegyeznünk, hogy a fizikusi (különösen a kisérleti részecskefizikusi) szóhasználat az ÉS áramkört nevezi "koincidenciának", tulajdonképpen pontatlanul. Egy n változós logikai függvény igazságtáblázatának 2 sora van. Függvényértékként 0-t vagy 1-et írhatunk, tehát az összes lehetséges különbözõ igazságtáblázatok száma:

$\begin{displaymath}2^{2^n}\quad .\end{displaymath}$

Ennek megfelelõen a lehetséges 4 változós függvények száma 65536. A kétváltozós Boole függvények közül néhány különösebb figyelmet érdemel. Az olyan függvények, melyek a bemeneti változók valamilyen logikai kapcsolatának negálását jelentik, (tehát az ÉS-NEM, VAGY-NEM) nyilvánvalóan felépíthetõk egy ÉS illetve VAGY áramkörbõl és egy inverterbõl. Ezeknek az egységeknek pedig az a rendkívül nevezetes tulajdonságuk, hogy velük mindhárom (ÉS, VAGY, invertálás) logikai alapmûvelet megvalósítható, tehát önmagukban alkalmasak logikai elemrendszer megvalósítására. Ennek a technikai jelentõsége elég nagy: gondoljuk meg, elegendõ csak NOR, vagy csak NAND áramköröket gyártani, hisz ezekkel is hiánytalanul felépíthetõ a "világ". Az elemek egységesítése egészen biztosan gyártási elõnyökkel jár, például a nagyobb sorozatok következtében a fajlagos elõállítási költség csökkenhet. A 6.3.2. táblázatban feltüntettünk néhány logikai elemrendszert és azt, hogy a logikai alapmûveletek velük miként valósíthatók meg. Az elemi mûveletek rendszerei között tehát választások adódnak, a gyakorlatban felhasznált áramköri elemek és technológiai lehetõségek alapján határozzák meg a kivitelezésre kerülõ logikai rendszerek alapmûveleteit.

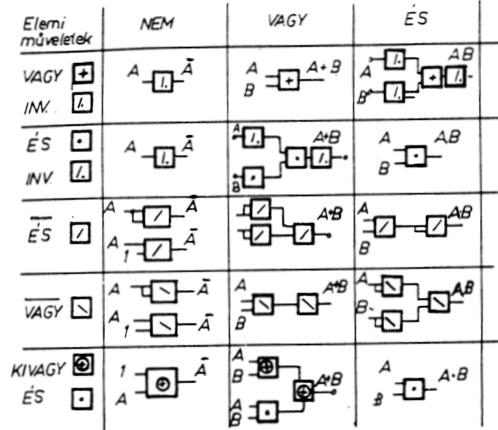
6.3.2. ábra
(Zárójelben jegyezzük meg, de egyáltalán nem másodrangú információ: az $A\cdot \bar{B}$ kétváltozós függvény is alkalmas mindenfajta logikai hálózat létrehozására. Ennek fontossága abban rejlik, hogy idegsejtjeink logikai mûködését leíró ún. McCullogh-Pitts féle modell lényegében ugyanezt a funkciót realizálja. Mindez azt is jelentheti, hogy a "Természet" eléggé racionálisan tervez és valósít meg, mésrészt pedig arra is utalhat, hogy mondjuk elektronikus NAND körökbõl is felépíthetõ egy olyan összetett szerkezet is, mint az emberi agy...)

Következõ: Boole függvények minimalizálása | Tartalomjegyzék | Elõzõ: Tartalomjegyzék

1999-09-23

			0	$A\cdot B$	$A\cdot \bar{B}$	A	$\bar{A}\cdot B$	B	$A\oplus B$	A+B
A	B	$\alpha$	0	1	2	3	4	5	6	7
0	0	$\alpha_0$	0	0	0	0	0	0	0	0
0	1	$\alpha_1$	0	0	0	0	1	1	1	1
1	0	$\alpha_2$	0	0	1	1	0	0	1	1
1	1	$\alpha_3$	0	1	0	1	0	1	0	1
					AND				XOR	OR

			$\bar{A}\cdot \bar{B}$	$\bar{A}\cdot \bar{B}+A\cdot B$	$\bar{B}$	$A+\bar{B}$	$\bar{A}$	$\bar{A}+B$	$\bar{A}+\bar{B}$	1
A	B	$\alpha$	8	9	10	11	12	13	14	15
0	0	$\alpha_0$	1	1	1	1	1	1	1	1
0	1	$\alpha_1$	0	0	0	0	1	1	1	1
1	0	$\alpha_2$	0	0	1	1	0	0	1	1
1	1	$\alpha_3$	0	1	0	1	0	1	0	1
			NOR	KOINC.					NAND