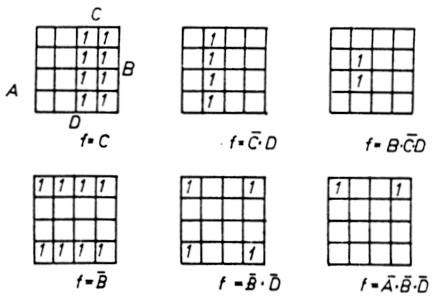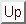
Következõ: Logikai függvények realizálása áramkörökkel | Tartalomjegyzék | Elõzõ: Kétváltozós Boole függvények

Boole függvények minimalizálása

Az elõzõekben már láttunk példát arra, hogy a Boole algebra szabályainak alkalmazásával az eredeti függvény egyszerûbb alakra hozható. Az "egyszerûbb" itt azt jelenti, hogy a függvényt kevesebb írásmunkával állíthatjuk elõ, ami nyilván azt is jelenti, hogy kevesebb logikai áramkörbõl kell építkeznünk. Az egyszerûsítés általában gazdasági és megbízhatósági elõnyökkel jár együtt. Az algebrai szabályok közvetlen ("hasra ütéses", heurisztikus) alkalmazása azonban csak kevés (2-3-4) változós függvények esetén használható: ha a bemenetek száma növekszik, a függvény áttekinthetetlenné válik, a mûveletek közben elkövetett hiba valószínûsége növekszik. Ezért különbözõ szemléletes, és könnyen mechanizálható eljárásokat dolgoztak ki az egyszerûsítések megkönnyítésére. E módszerek egyike az ún. Veitch-Karnaugh módszer. Lényege egy diagram, melybe az igazságtáblázat közvetlenül berajzolható, mert a diagramot alkotó négyzetek egy-egy kanonikus tényezõnek felelnek meg.

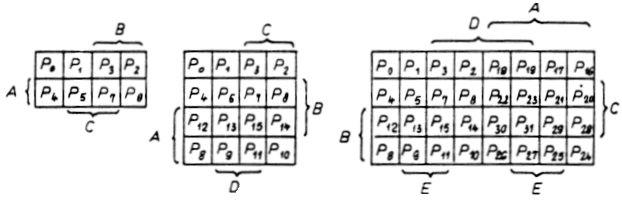
6.4.1. ábra

A 6.4.1. ábra az n = 3,4,5 változóra felrajzolható diagramokat mutatja. A 6.4.2. ábrán feltüntettünk néhány elemi tényezõnek (változók szorzata, de nem feltétlenül szerepel benne az összes változó) a Veitch diagramon történõ elhelyezését. Az ábrák vizsgálatából kiderül, hogy a kanonikus tényezõknek egyetlen kis négyzet felel meg, az elemi tényezõknek pedig 2,4,8 vagyis annál több, minél kevesebb változó szerepel benne. Észre kell vennünk azt is, hogy ilyenkor az 1-et tartalmazó négyzetek mindig egymás mellett helyezkednek el, természetesen csak akkor, ha a diagramot függõleges és vízszintes határoló vonalai mellett "összeragasztva" képzeljük el. (A diagram tehát egy tóruszon helyezkedik el.)

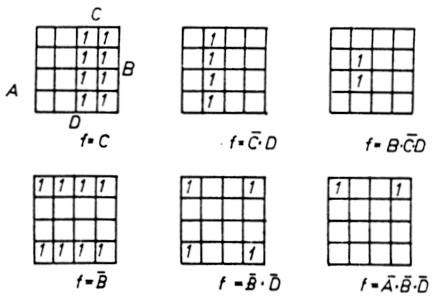
6.4.2. ábra
A kanonikus alakban megadott Boole függvények minimalizálása a fentiek alapján tehát azt jelenti, hogy a diagramon feltüntetjük a lehetséges elemi tényezõket úgy, hogy minél több 1-et lehessen egymás mellett levõnek tekinteni. Ez ugyanis az elemi tényezõket realizáló logikai áramkörök bemeneteinek számát (ÉS, VAGY áramkörnél a diódák számát) csökkenti. Példaképpen a 6.4.3. ábrára utalva minimalizáljuk az

f =P₃+P₇+P₈+P₉+P₁₂+P₁₃+P₁₅

függvényt.

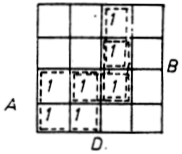
6.4.3. ábra

A megoldás láthatóan nem egyértelmû: függ attól, hogy melyik 1-eket tekintjük összetartozóknak:

$\begin{displaymath}f_1=A\cdot \bar{C}+\bar{A}\cdot C\cdot D+B\cdot C\cdot D\quad,\end{displaymath}$

$\begin{displaymath}f_2=A\cdot \bar{C}+\bar{A}\cdot C\cdot D+A\cdot B\cdot D\quad.\end{displaymath}$

A két függvény realizáláshoz szükséges bemenetek száma azonban azonos. A Veitch-Karnaugh diagram használata tehát igen egyszerû, és eredményül elemi tényezõk összegeként kapjuk a végeredményt. Természetesen az S tényezõkre teljesen szimmetrikusan hasonló egyszerûsítési szabályok vezethetõk le. A Veitch diagram módszernek igen szemléletes voltából még egy további elõny fakad. Ennél az eljárásnál ugyanis az ún. "közömbös" tényezõk figyelembevétele nagyon könnyû. Közömbös tényezõnek tekintünk olyan bemeneti változó kombinációt (P tagot), amely a mûködés során nem jöhet létre, vagy a létrejöttekor kialakuló kimeneti függvény értéket nem használjuk. Közömbös tényezõ pl. a 4 bistabilból felépített BCD számlálóban (Binary Coded Decimal - binárisan kódolt decimális - vagyis csak a 0 - 9 számok fordulnak elõ, az ennél nagyobbak nem) az 1010, 1011... kombináció. Ha az elõzõ példánkban az ABCD kombináció nem jöhet létre, az eredeti függvény sokkal radikálisabban egyszerûsíthetõ:

$\begin{displaymath}f_3=A\cdot \bar{C}+C\cdot D\quad .\end{displaymath}$

A Boole függvények egyszerûsítésének tehát vannak nagyon szemléletes és gyorsan eredményre vezetõ módszerei. Az "egyszerû" alakra való törekvés azonban nem egyértelmû. Számos függvény ugyanis egyszerûbb alakra hozható, ha nem elemi tényezõk összegeként, vagy szorzataként írjuk fel õket. Ez persze azzal jár, hogy az ún. kétfokozatú logika helyett több fokozatút használunk, vagyis a bemenõjel a kimenetig nem csak két kapurendszeren (egy ÉS és egy VAGY) jut a kimenetre, hanem több fokozaton keresztül. A fokozatok számának növekedése pedig a bemenõjel és a kimenõjel közötti - esetleg tetemes - idõkésést eredményez, ami a logikai kimenet idõlegesen helytelen értékében is megnyilvánulhat. Gondot okozhat az is, hogy az egyszerûsítési eljárás ÉS, VAGY áramkörökre ugyan minimalizálja a bemenet számát, de ha rendelkezésünkre 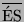$\overline{\rm\acute{E}S}$ illetve 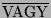$\overline{\rm VAGY}$ áramkörök állnak, már némileg eltérõ módon kell az áramkört realizálni. Nem szabad elfeledkezni arról sem, hogy a ténylegesen kivitelezett logikai áramkörök kimenetei nem terhelhetõk korlátlanul. Logikailag helyes összefüggést éppen ezért nem biztos, hogy a rendelkezésre álló rendszerekkel közvetlenül meg lehet valósítani. Inverterek, emitterkövetõk, teljesítményerõsítõk elhelyezését pedig az egyszerûsítõ eljárások nem adják meg. Lehetséges az is, hogy a bemenõ változók egy adott csoportjához több kimenõ függvény is tartozik. A több kimenetû függvények egyszerûsítése pedig - a közös részek keresése - az ismertetett módszertõl eltérõ eljárást igényel. Logikai függvények "kézi" egyszerûsítéséhez csak a legegyszerûbb esetekben folyamodjunk. Összetettebb problémák megoldásához használjunk számítógépet: nagyszámú, igen hatékony program létezik, amelyek gyorsan és fáradság mentesen szolgáltatnak eredményt.

Következõ: Logikai függvények realizálása áramkörökkel | Tartalomjegyzék | Elõzõ: Kétváltozós Boole függvények

1999-09-23