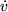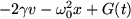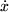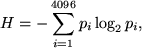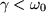A mérés célja, hogy bevezetést adjon a modern fizika egyik érdekes ágába, a káosz-elméletbe: olyan egyszerű (-nek tűnő!) fizikai rendszert vizsgálunk, amelyen az elméletben szereplő mennyiségek és összefüggések egyszerű eszközökkel kimérhetők.

Naivan azt gondolhatnánk, hogy minden "összevissza" viselkedő rendszer kaotikus. Ez nem így van, egy kaotikus rendszernek bizonyos különleges tulajdonságai vannak. Ebben a fejezetben ezekkel foglalkozunk, röviden áttekintve az elmélet fogalmait.

Vegyünk példának egy egyszerű klasszikus mechanikai rendszert: a csillapított harmonikus oszcillátort [1, 18.§.]. A mozgásegyenlet :

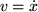) esettel foglalkozunk. Hasznos bevezetni a sebesség változót ( $v=dot x$

), így az (1) egyenlet a következő alakú lesz:

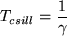
$begin{displaymath}T_{csill} = {1over gamma}end{displaymath}$

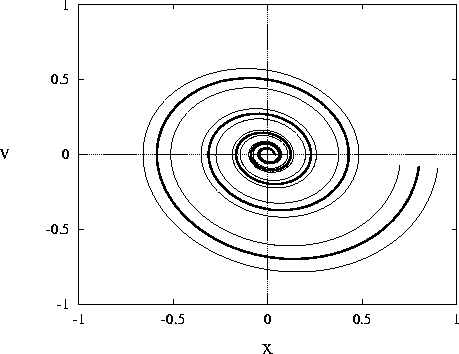
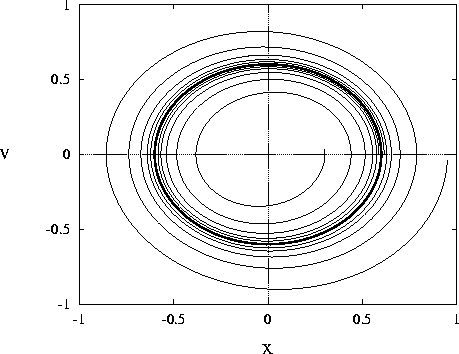
idő alatt lecsillapodik a rezgése. Ezt a folyamatot legáttekinthetőbben az (x,v) síkon ábrázolhatjuk: rajzoljuk fel a (x(t),v(t)) paraméteres görbét (1 ábra). Az (x,v) sík a rendszer fázistere, az görbe pedig a trajektória, amit a rendszer befut az (x₀,0)kezdőállapotból indítva. Látható, hogy a végállapot (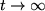 $ttoinfty$ ) minden esetben a (0,0) pont, az ilyen tulajdonságú pontot nevezzük stabil fixpontnak. Léteznek instabil fixpontok is, azokból tetszőlegesen kis mértékben kitérítve a rendszert az nem tér vissza oda. Például 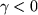$gamma<0$ esetben, azaz ha nem csillapított, hanem öngerjesztő az oszcillátor, akkor a (0,0) pont továbbra is fixpont marad, de a stabilitását elveszti.

begin{figure}centerline{psfig{figure=f9.eps,height=3in}}bigskipsmallskipend{figure}

1. ábra: A csillapított oszcillátor trajektóriái

Vizsgáljuk meg mi történik, ha G(t) külső gerjesztő erővel hatunk az oszcillátorunkra. A (2) egyenlet a következőre módosul:

	=
		=		V	(3)

Ha speciálisan 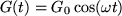$G(t) = G_0 cos(omega t)$ , akkor a rendszer 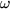$omega$ frekvenciájú harmonikus rezgést fog végezni

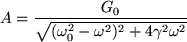
$begin{displaymath}A= {G_0over{sqrt{ (omega_0^2-omega^2)^2+4gamma^2omega^2}}} end{displaymath}$

amplitúdóval. A fázistérben ennek a mozgásnak a trajektóriája egy ellipszis A illetve 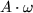$A cdotomega$ nagytengelyekkel (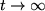2 ábra). Meg lehet mutatni, hogy ez a mozgás stabil, azaz ha a fázistér olyan pontjából indítjuk a rendszert, amely nincs rajta ezen az ellipszisen, akkor az onnan induló trajektória $ttoinfty$ esetben az ellipszishez fog hozzásimulni. A fázistér ilyen tulajdonságú görbéjét nevezzük határciklusnak. Általában, azt a halmazt, amelyhez a trajektóriák tartanak attraktornak (azaz ``vonzó''-nak) nevezzük. Így például a stabil fixpont és a határciklus egyaránt attraktor.

begin{figure}begin{center}psfig{figure=f7.eps,height=3in}end{center}smallskipend{figure}

2. ábra: A harmonikusan gerjesztett csillapított oszcillátor trajektóriái

Az (1) egyenlet egy lineáris rendszert ír le, egy valós fizikai rendszer esetében x-ben magasabbrendű tagok is megjelenhetnek, azaz a probléma nemlineárissá válhat. Ebben az esetben analitikus megoldás nem lehetséges, csak mérés illetve az egyenletek numerikus megoldása útján vizsgálhatjuk a rendszer viselkedését. Az eredmény sokszor rendezetlen (kaotikus) mozgás, szemben a lineáris eset hosszú távra előre jósolható mozgásaival. A lineáris egyenlettel leírható rendszerben ugyanis valamely $tau$ időpillanatban mért mennyiség hibája a kezdőfeltételek hibájával arányos: a közeli trajektóriák időben lineárisan távolodnak. A kaotikus rendszerekben a jósolhatóság hiányát az okozza, hogy a fázistér két egymáshoz közeli pontjából induló trajektóriák exponenciálisan távolodnak, azaz tetszőlegesen kicsi eltérés a kezdőfeltételtől véges idő alatt makroszkópikus különbséget okoz a fejlődésben. Ez a kaotikus rendszerek egyik leglényegesebb jellemzője, és azzal a következménnyel jár, hogy a rendszert csak valószínűségi (statisztikus) módszerekkel tudjuk kezelni, annak ellenére, hogy nem rendelkezik olyan sok szabadsági fokkal, mint egy tipikus statisztikus rendszer.

Természetesen ekkor is létezhetnek a fázistérben attraktorok, de azok általában nem egyszerű alakzatok, hanem tört dimenzióval rendelkeznek (fraktálok), ezért őket különös attraktoroknak (strange attractor) nevezzük.

Az eddigiekben a csillapodó mozgás jellemzésére a fázistérbeli trajektóriáját használtuk. Található-e a csillapodásnak egy kevesebb információt hordozó jellemzése úgy, hogy azért a folyamatra vonatkozó lényeges információt nem vesztünk el? Az, hogy egy mozgás csillapodik az megfelel annak, hogy az egymást követő maximális kitérések nagysága csökken. A maximális kitéréseknek megfelelő pontok a fázistérben a trajektória és a pozitív x tengely metszéspontjai. Egy ilyen metszéskor a sebesség nulla, előtte pozitív, utána pedig negatív: következésképpen x-nek tényleg maximuma van ebben a pontban. Ezek szerint tehát jól jellemezhetjük a mozgást ezekkel a metszéspontokkal 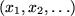$(x_1,x_2,dots)$ , amelyeket a trajektória és az x tengely Poincaré-metszetének nevezünk. Fontos megjegyezni, hogy a negatív x tengellyel vett metszéspontok nem tartoznak a Poincaré-metszethez. Az általános definíció szerint a trajektória és a fázistér dimenziószámánál egyel kisebb dimenziójú sík egyirányú metszéspontjai, azaz ebben az esetben (d=2) egy egyenessel vett metszéspontok közül azok, amelyekben felülről lefelé történik a metszés.

A folytonos trajektóriához hozzárendeltük tehát a diszkrét x_i sorozatot. A mozgásegyenleteknek ekkor valamilyen F leképezés felel meg:

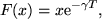
$begin{displaymath}F(x) = x {rm e}^{-gamma T},end{displaymath}$

ahol T a rendszer periódusideje, ugyanis egy periódus alatt éppen 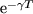${rm e}^{-gamma T}$ részére csökken a rezgés amplitúdója. Általános esetben ez a leképezés nem írható fel analitikus alakban, hanem közelítésekkel kell élnünk.

Vizsgáljuk meg például a populációdinamika legegyszerűbb modelljét: nyulak és rókák együttélésének egyszerű közelítését. Legyen x_n az n-edik évben élő nyulak számával arányos mennyiség, úgy normálva, hogy 0 és 1 közé essen. A rákövetkező évben a nyulak száma legyen

1, akkor a következő évben kevés nyúl lesz (ugyanis a rókák megeszik őket). Ezt a leképezést nevezi az irodalom logisztikus leképezésnek [2,3].

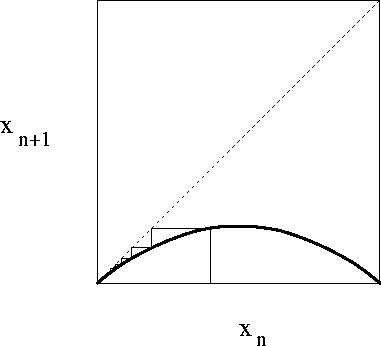
begin{figure}begin{center}psfig{figure=kjf1.eps,height=3in}bigskipparend{center}end{figure}

3. ábra: A logisztikus leképezés viselkedése r=0.8 esetén

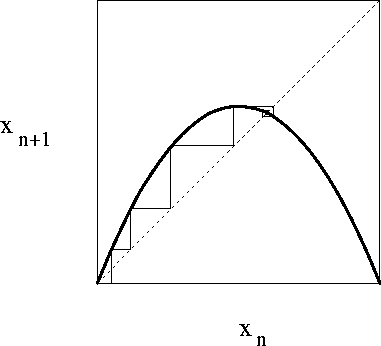
begin{figure}begin{center}psfig{figure=kjf2.eps,height=3in}end{center}end{figure}

4. ábra: A logisztikus leképezés viselkedése r=2.8 esetén

Ha r<1=r₁, akkor minden kezdőállapotból indítva x_n ->0 (3 ábra), ez a rendszer egyedüli fixpontja (x₁^*). Ha r-et 1 fölé növeljük, akkor megjelenik egy másik fixpont is: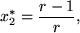

$begin{displaymath}x_2^* = {{r-1}over r},end{displaymath}$

és ezzel egyidőben x₁^* instabillá válik (4 ábra). Egyszerűen kiszámítható, hogy van olyan r₂(=3), hogy r>r₂ értékekre x₂^* is instabil lesz. Ekkor azonban F második iteráltjának

F⁽²⁾(x) = F(F(x))

megjelenik két stabil fixpontja ( x₃^*, x₄^*). Az attraktort ez a két fixpont fogja alkotni, és mivel

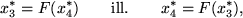
$begin{displaymath}x_3^* = F(x_4^*) qquad {rm ill.} qquad x_4^* = F(x_3^*),end{displaymath}$

ezért a nyulak száma két éves periódussal oszcillálni fog. Ezt a változást az időfejlődésben, azaz a periódusidő hirtelen 1 év 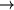$to$ 2 év átmenetét, nevezzük bifurkációnak. r-et tovább növelve egyre nagyobb periódushosszú lesz az attraktor ( 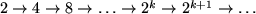$2to4to8todotsto2^kto2^{k+1}todots$ ), végül egy kritikus

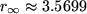
$begin{displaymath}r_inftyapprox 3.5699end{displaymath}$

értéknél ez a hossz divergál: a rendszer kaotikus lesz. Ez a bifurkáció sorozat a kaotikussá válás egyik leggyakrabban előforduló módja és Feigenbaum-szekvenciának nevezik.

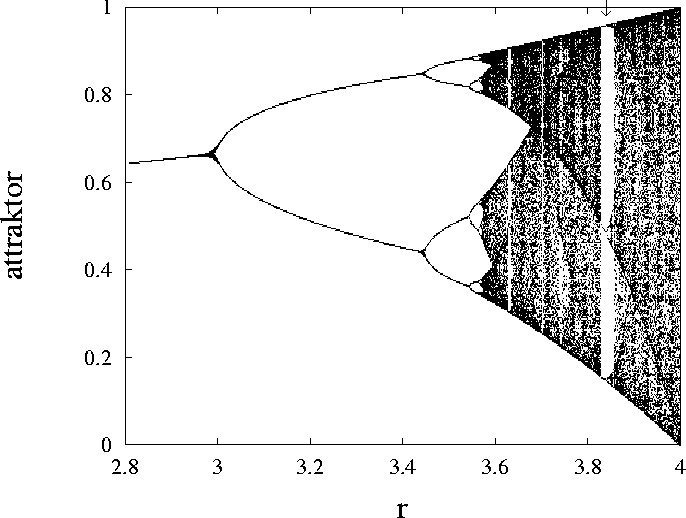begin{figure}begin{center}psfig{figure=kjf3a.ps,height=3in}end{center}end{figure}

5. ábra: A logisztikus leképezés bifurkációs diagramja

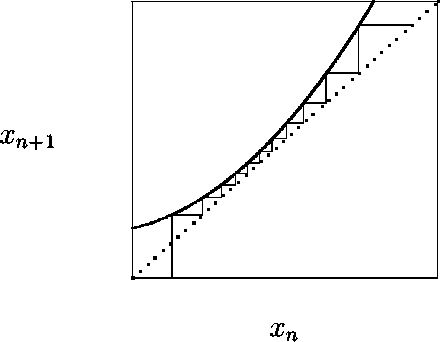
Numerikus mérések és később az analitikus meggondolások azt mutatták, hogy minden olyan leképezésre, amelyben a logisztikushoz hasonlóan az F függvénynek négyzetes maximuma van (azaz pl. nem hegyes), létezik a

(r=3.8281)

Ehhez kapcsolódik még egy érdekes jelenség: az intermittencia. Ez azt jelenti, hogy bizonyos paraméter értékeknél a kaotikus tartományban is sokáig szabályosan viselkedik a rendszer , majd átvált kaotikussá (6 ábra). Egy idő múlva ismét visszatér a szabályos viselkedés és ez így ismétlődik tovább. A magyarázatot a 7 ábrán láthatjuk: az iteráció belejut egy ilyen ``csőbe'' és nagyon sokáig tart, amíg átjut rajta. Amíg a csőben tartózkodik, az x_n értékek alig változnak, azaz olyan mintha szabályos lenne a rendszer. Amint kijut belőle, újra a kaotikus trajektória mentén fog mozogni, majd bolyongása során megint visszajut a csőbe.

Összefoglalva:

áttekintettük a káosz-elméletben (is) használatos fogalmakat:

fázistér, trajektória, fixpont, stabilitás, határciklus, attraktor, Poincaré-metszet, leképezés, bifurkáció, Feigenbaum-szekvencia, univerzalitás, intermittencia;

főbb vonalaiban bemutattuk a logisztikus leképezés viselkedését, a káosz kialakulását és tulajdonságait.

begin{figure}begin{center}centerline{psfig{figure=f5.eps,height=3in}}bigskipend{center}end{figure}

7. ábra: Intermittencia kialakulása egy leképezésben

Az áramkör

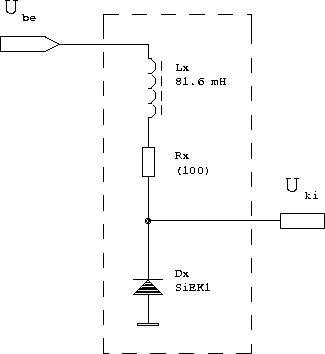
Vizsgálataink tárgyát a lehető legegyszerűbb nemlineáris elektronikus áramkör képezi (8 ábra): egy veszteséges tekercs (L_xR_x) és egy szilícium egyenirányító dióda (D_x) sorba kapcsolva. A rendszer bemenete a tekercs egyik kivezetése, a kimenete pedig a dióda katód elektródja. Ez az áramkör a bevezetésben említett csillapított oszcillátor nemlineáris változatának elektronikus megfelelője, tulajdonságait az elmúlt tíz évben részletesen vizsgálták [5,6].

begin{figure}centerline{psfig{figure=kaosz0.ps,height=3.2in,bbllx=2.2in,bblly=7.7in,bburx=4.8in,bbury=10.2in,clip=}}end{figure}

8. ábra: A kaotikus áramkör

Ha egyenfeszültséget adunk a bemenetre, akkor a jól ismert dióda karakterisztika miatt

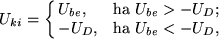
$begin{displaymath}U_{ki} = cases {U_{be}$

ahol 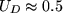$U_Dapprox 0.5$ V, a dióda nyitófeszültsége. Mindez igaz abban az esetben is, ha a bemenő feszültség frekvenciája nem túl nagy (f<1 kHz). Ebben a tartományban az áramkör belső tranziensei sokkal gyorsabban lecsengenek, mint a gerjesztés periódusideje. Ezen tranziensek idejét két jelenség határozza meg, amelyek megértéséhez túl kell lépni a sztatikus diódamodellen:

a záróirányban előfeszített dióda záróréteg kapacitása a tekerccsel és annak belső ellenállásával egy soros RLC kört képez (ld. 1. feladat);

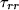a dióda véges lezárási késleltetési ideje ( $tau_{rr}$ , reverse recovery time) [4].

Az első hatás két jellemző időskálát jelent. A kör rezonancia frekvenciájához tartozó periódusidő

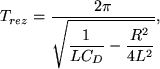
$begin{displaymath}T_{rez} ={2piover{displaystylesqrt{ {1over{LC_D}}-{R^2over{4L^2}} }}},end{displaymath}$

ahol C_D a dióda záróirányú kapacitása, és

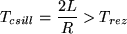
$begin{displaymath}T_{csill} = {2Lover R}$

a rezgések lecsengési ideje. A diódának ez a tulajdonsága önmagában nem elegendő kaotikus viselkedés létrejöttéhez.

A késleltetési időt az okozza, hogy a dióda lezárásához a pn átmenetből ki kell ürülniük a jelenlevő töltéshordozóknak. Ez abban nyilvánul meg, hogy miközben már záróirányú feszültség esik a diódán,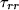 $tau_{rr}$ ideig még nyitóirányú áram folyik rajta. Közönséges alkalmazásokban, jól megválasztott diódatípus felhasználása mellett ezt az időt el lehet hanyagolni, itt azonban fontos szerepet játszik. Ezt az időt nagyban befolyásolja a dióda geometriája és a nyitóáram értéke. A gyors ( 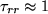$tau_{rr}approx 1$ ns) diódák kis méretűek, kicsi a felületük, következésképpen a töltéshordozók gyorsan ki tudnak diffundálni az átmenetből. Ha a gyorsaság helyett a disszipált teljesítményen van a hangsúly (pl. hálózati egyenirányító diódákra tipikusan I_max=1…10 A), akkor nagy méretű diódát alkalmaznak, ellenkező esetben könnyen túlmelegedne. Az áramkörben felhasznált SiEK1 diódára a nyitóáramtól függően

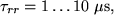
$begin{displaymath}tau_{rr} = 1dots 10~mu{rm s},end{displaymath}$

ami viszonylag nagy érték. A záróirányú kapacitással együtt ez a késleltetési idő az, ami a kaotikus viselkedést okozza ebben az áramkörben. Ha gyors diódát alkalmazunk, akkor nem kapunk kaotikus kimenő jelet. Ez azt mutatja, hogy nagyon fontos szempont egy áramkör tervezésénél az áramköri elemek paramétereinek gondos figyelembevétele, hiszen könnyen kaphatunk kaotikus viselkedést, ami rendkívül zajossá teszi a kimeneti jelet.

Ha a kaotikus áramkör bemeneti frekvenciája eléri a 10 kHz-es nagyságrendet, akkor a bemeneti amplitúdót fokozatosan növelve az egy nagyságrendbe eső időskálák (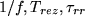 $1/f, T_{rez}, tau_{rr}$ ) miatt nemlineáris rezonancia lép fel a rendszerben (ld. 2. feladat). Ennek a hatására egy kritikus bemenő amplitúdónál bifurkációt figyelhetünk meg, majd tovább növelve az amplitúdót Feigenbaum-szekvencia után a jel kaotikus lesz (ld. 3. feladat). Előállíthatunk intermittens viselkedést és szépen megfigyelhető a 6-os és 3-as periodikus ablak is. Ennek ellenére nem a logisztikus leképezés írja le az áramkört (ld. 5. feladat), ez pontosan az univerzalitás megnyilvánulása: az áramkör pontos viselkedését ugyan nem adja meg a logisztikus leképezés, mégis jó modell a káosz kialakulása körüli viselkedés megértésére. A mérések szerint az áramkör legjobban egy kétdimenziós (kétváltozós) leképezés írja le.

A mérőelőtét és a mérőprogram

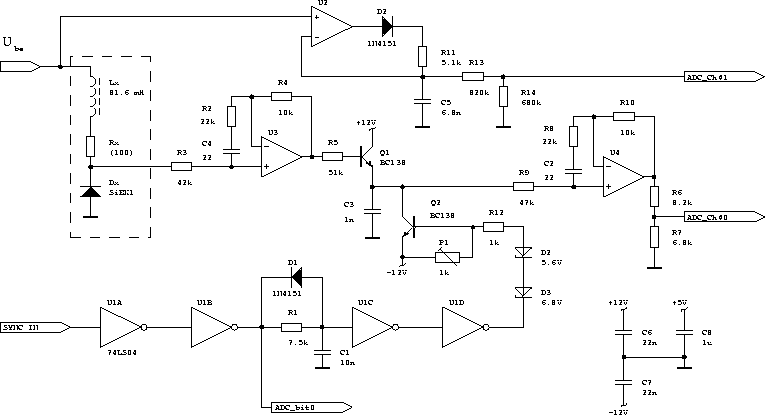
Az áramkör viselkedését legegyszerűbben oszcilloszkópon figyelhetjuk meg, de az nem alkalmazható kvantitatív mérésekre. Erre a célra egy IBM PC számítógépen alapuló mérőrendszer szolgál: a kaotikus áramkör jele a merőelőtétbe jut, onnan egy 12 bites analóg-digitális konverter kártyára, amelynek kimenetét a mérőprogram dolgozza fel.

A mérőelőtét

Hasonlóan az első fejezetben leírtakhoz, célszerű a kaotikus jel Poincaré-leképezését vizsgálni a teljes jel helyett. Ez a gyakorlatban azt jelenti, hogy csak a jel maximumainak értékére vagyunk kiváncsiak, ezen maximumok meghatározását végzi a mérőelőtét (9 ábra), amely három fő részből áll:

folytonos üzemű csúcsegyenirányító;

mintavételező csúcsegyenirányító;

kisütő- és szinkronjel generátor.

begin{figure}centerline{psfig{figure=kaosz3a.ps,height=7in,bbllx=-10.8in,bblly=0.5in,bburx=-6.3in,bbury=8.5in,clip=}}end{figure}

9. ábra: A mérőelőtét kapcsolási rajza

Az U₂ műveleti erősítővel felépített folytonos üzemű csúcsegyenirányító a bementi jel amplitúdójának mérésére szolgál. Az R₁₃ - R₁₄ ellenállásokkal felépített osztó a maximálisan 10 - 12 V-os kimenő szintet igazítja az A/D konverter max. 5 V bemeneti feszültségéhez.

A mintavételező csúcsegyenirányító az U₃ és U₄ műveleti erősítőkből áll, ennek a feladata a kaotikus jel csúcsértékeinek meghatározása. Itt nem az előzőleg alkalmazott visszacsatolt kapcsolást választottuk, mert sajnos annak tranziens tulajdonságai nem voltak elég jók. Helyette kompromisszumot kötöttünk a pontosság és a gyorsaság között, és egy egyszerű passzív csúcsegyenirányítót használunk. Az U₃-mal felépített egységnyi erősítésű fokozat nagy bemenő ellenállása révén alig terheljük a kaotikus áramkört. Az R₅ ellenálláson keresztül a Q₁ tranzisztort vezéreljük, amely egyrészt a bázis-emitter dióda és C₃ miatt csúcsegyenirányítóként működik, másrészt áramerősítést végez, ami ahhoz szükséges, hogy követni tudjuk a bemeneti feszültség (azaz a kaotikus áramkör kimeneti feszültégének) változását. Mivel a kondenzátor töltése Q=CU, ezért a kondezátor feszültségének időbeli változása: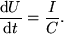

begin{displaymath}{{rm d} Uover{{rm d} t}}= {Iover C}.end{displaymath}

Ha dU/dt (amit slew-rate-nek neveznek) kisebb, mint a bemeneti feszültség változási gyorsasága, akkor a kimeneti feszültség értéke hibás lesz. Nagyobb slew-rate-t pedig csak nagyobb áramerősséggel tudunk elérni, ezért van szükség a Q₁ tranzisztor áramerősítésére. A visszacsatolás nélküli egyenirányító kimeneti feszültsége sajnos egy diódafeszültséggel (U_D) kisebb mint a bemenő csúcs feszültsége, mérési pontatlanságot okoz ennek a különbségnek emitteráram függése. A kondenzátor feszültségét az U₄-gyel kialakított feszültségkövető és az R₆ - R₇ osztó illeszti az A/D átalakítóhoz.

A kisütő- és szinkronjelet egy 74LS04 (6 x NOT) digitális IC segítségével állítjuk elő a funkciógenerátor kimenő szinkronjeléből. A kisütés úgy van időzítve (R₁C₁), hogy a kaotikus jel maximuma és az A/D konverzió lezajlása után (ez kb. 13 usec) süsse csak ki a Q₂ tranzisztor C₃-t. A kondenzátort nem földpotenciálra sütjük ki, hanem valamilyen negatív potenciálra. Ez azért szükséges, hogy U_D-nél kisebb maximumokat is ki tudjunk mérni. A kisütés mértékét a P₁ trimmer potenciométerrel változtathatjuk, az a jó beállítás, ha a legnagyobb bemenő csúcs után is negatívba megy a kondezátor feszültsége.

A mérőprogram

A mérőprogram három kiértékelő programból áll, amelyek különböző feladatokat látnak el. Ezek közül egy egyszerű menü segítségével választhatunk.

Oszcilloszkóp

Ebben az üzemmódban közvetlenül figyelhetjük meg az A/D átalakítóról érkező jelet. Itt jeleníthetjük meg a bifurkációkat és a kaotikus tartományba ágyazott periodikus ablakokat. A mért adatok elmenthetők, majd például a gnuplot programmal könnyen ábrázolhatók.

Az egyes billentyűk funkciója:

SPACE a kijelzés leállítása (``tároló szkóp''); ENTER folyamatos kijelzés; + ill. - az erősítés növelése illetve csökkentése; S az adatok kimentése; ESC vissza a főmenühöz.
Attraktor

Ez az üzemmód a rendszer Poincaré-metszetbeli attraktorának vizsgálatára szolgál.

A mérésből rendelkezésünkre áll egy x_n sorozat, ábrázoljuk x_n+1-t x_n függvényében. Ha a rendszert egy egyszerű leképezés írja le, akkor (4) alapján az F függvénynek kell kirajzolódnia. Ha bonyolultabb a helyzet, akkor a kirajzolódó alakzat nem lesz egyértékű függvénnyel jellemezhető. Viszont maga az alakzat mindenképpen a rendszer attraktorát jellemzi: a periodikus szakaszban egy vagy néhány pontot, a kaotikus állapotban pedig folytonos görbét kapunk. Az (x_n, x_n+1) pontok ábrázolásával könnyen különbséget lehet tenni teljesen véletlen és kaotikus jel között: véletlen jelre a módszer nem egy görbét, hanem egy betöltött síkidomot szolgáltat (azaz például betölti az egész négyzetet).

A programmal változtathatjuk a késleltetést, x_n+j-t ábrázolhatjuk x_n függvényében (j=1..9).

Az egyes billentyűk funkciója:

ENTER az ábra törlése; + ill. - az erősítés növelése illetve csökkentése;

$Leftarrow$ ill. a késleltetés csökkentése illetve növelése;

S az adatok kimentése; ESC vissza a főmenühöz.
Eloszlás

Ebben az üzemmódban az A/D átalakítóról érkező jelek nagyság szerinti eloszlását vizsgálhatjuk. Periodikus viselkedés mellett csak egy vagy néhány amplitúdó értéket mérünk, ha viszont kaotikus a rendszer, akkor széles tartományban változnak a mért csúcsok amplitúdói.

A kimentésnél itt csak egyszer kell megadni a file nevét, utána minden kimentett eloszlás ugyanabba a fileba kerül. Így könnyen fel lehet venni a bifurkációs diagramot: különböző bemenő feszültségeknél felvett eloszlásokat kell egymás után kimenteni. A program kiszámítja a megmért eloszláshoz tartozó információt is: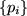

$begin{displaymath}H = - sum_{i=1}^{4096} p_i log_2 p_i,end{displaymath}$

(7)

ahol ${p_i}$ a mért eloszlás. Ez az információ éles eloszlásokra kicsi, maximális értékét ( H_max= 12 bit) pedig az egyenletes eloszláson veszi fel. Egy bifurkáció során H elméletileg 1 bittel nő, de ebben a rendszerben a jelenlevő zaj miatt ez a növekmény kevesebb. A kimentett adatfile harmadik oszlopában található az információ értéke.

Az egyes billentyűk funkciója:

SPACE új mérés indítása; + ill. - az erősítés növelése illetve csökkentése; S az adatok kimentése; ESC vissza a főmenühöz.
Irodalomjegyzék

1 Budó Á. : Mechanika (Tankönyvkiadó, 1988)

2 A káosz (szerk.: Szépfalusy P. és Tél T.; Akadémiai Kiadó, 1982)

3 H. G. Schuster : Deterministic Chaos (Physik-Verlag, 1984)

4 U. Tietze, Ch. Schenk : Analóg és digitális áramkörök (Műszaki Kiadó, 1990)

5 P. S. Linsay : ``Period doubling and chaotic behaviour in a driven anharmonic oscillator'', Phys. Rev. Lett. 47, 1349, (1981).

6 Z. Su, R.W. Rollins, E.R. Hunt : ``Simulation and characterization of strange attractor in driven diode resonator systems'', Phys. Rev. A 40, 2698, (1989).

Feladatok

Adjon az áramkör bemenetére 1 V amplitúdójú 1 kHz frekvenciájú négyszögjelet. Vizsgálja meg az oszcilloszkópon a diódán kialakuló feszültséget. A rezgések periódusidejéből határozzuk meg az RLC kör rezonanciafrekvenciáját.Adja meg ezt a frekvenciát. Mekkora a dióda záróirányú kapacitása?

30 kHz-es szinuszos bemenő feszültség amplitúdóját fokozatosan növelve figyelje meg az oszcilloszkópon a kimeneti jelalak változását. A számítógépes mérőprogrammal készítsen felvételeket a bifurkálódó, a kaotikus tartományban és a periodikus ablakban tartózkodó rendszerről, valamint az intermittens jelekről! Az ábrákat (feliratozva) csatolja a jegyzőkönyvhöz! Megj.: a S(ave) utasítással elmentett adatokat a gnuplot programmal tudja kirajzoltatni. Pl. a plot 'j32.khz', 'j33.khz'

utasítással a j32.khz és a j33.khz file-t együtt rajzoltathatja ki. Nyomtatáshoz a plot parancs előtt adja ki a

set term postscript

set out 'lpt1'

utasításokat, majd a plot parancs után a set output parancsot!

Állítsunk be egy frekvenciát a 30 - 35 kHz-es tartományból. Színuszos bemenő jel mellett vegyük fel az attraktor és a (7) szerinti információ feszültségfüggését, és a mért értékeket adja meg:

Az előző adatok alapján válasszon olyan frekvenciát, ahol a legtovább tud elmenni a kaotikus tartományban! Mekkora ez a frekvencia?

Határozza meg a bifurkációs pontokhoz (r_k) tartozó bemeneti feszültség értékeket (legalább k=3 -ig):

Mennyire teljesül a (6) összefüggés? Mit állapíthat meg az adatok alapján?

A 10 … 40 kHz frekvenciatartományban mérjük meg az első bifurkációs feszültség frekvenciafüggését legalább 6 pontban, és ábrázolja grafikusan is!:

Mérjük meg kaotikus állapotban a rendszer Poincaré-leképezésbeli attraktorát! A kinyomtatott ábrát csatlja a jegyzőkönyvhöz!

Hogyan lehetne nagy periódushosszú periodikus pályákat kimérni a Feigenbaum-szekvenciában?