Következõ : Emitterkövetõ, közös kollektorú erõsítõ | Tartalomjegyzék | Elõzõ : Közös emitterû erõsítõ

Emitterellenállást is tartalmazó erõsítõ

Az 1.3.1. ábrán olyan áramkört látunk, amely az elõzõhöz hasonló, de kissé bonyolultabb: azzá teszi az emitterellenállás.

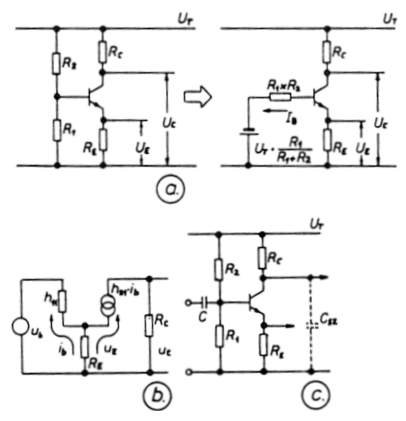
1.3.1. ábra

Tekintsük elõször feladatunknak a tranzisztor elektródáin található nyugalmi egyenfeszültségek meghatározását (1.3.1.a ábra). A bázisosztó a Thevenin tétel segítségével egyszerûsíthetõ. A tranzisztor U_D bázis-emitter feszültségét - hallgatólagosan állandó - értékûnek tekintjük, amelyrõl tudjuk, hogy kb. 0.6-0.8 V nagyságú. (Ez természetesen csak közelítés, amire azért van szükség, hogy ne kelljen a tranzisztort leiró transzcendens egyeletrendszer megoldásával piszmogni. Fokozottabb pontosság-igények esetén a ma már könnyen elérhetõ számítógépes áramköranalizáló programokat kell használni.) Vegyük észre: a tranzisztor állapotát (áramát) a bázisfeszültség és az emitterfeszültség különbsége szabja meg. Elsõként tehát ezeket kell meghatároznunk. A bemenõkörre felírt, a nyugalmi állapotra vonatkozó egyenletek két ismeretlent tartalmaznak, I_B-t és U_E -t:

$\begin{displaymath}U_T {R_1\over R_1 + R_2} = I_B R_1 \times R_2 + U_D + U_E\end{displaymath}$

U_E = I_E R_E

U_E -rõl azonban tudjuk, hogy ezt az R_E ellenálláson az

I_E = I_B+I_C = I_B(h₂₁+1)

nagyságú áram hozza létre. A két alapegyenletbol egyértelmûen& meghatározhatjuk I_B értékét, amibõl azután I_E és I_C a tranzisztor alaptulajdonságaiból kiadódik:

$\begin{displaymath}I_E = (h_{21}+1) I_B \qquad \qquad \qquad I_C = h_{21}I_B \quad ,\end{displaymath}$

és eljuthatunk U_E és U_C meghatározásához. (Tudatosan nem írtunk több képletet, mert túl hosszú lenne és az áramkör fizikáját elfedné. A lényeg a számítási módszer: az egyenletek felírásának sorrendje, az elhanyagolások.) A váltakozóáramú, vagy differenciális helyettesítõ kép segítségével (1.3.1.b. ábra) az elõzõkhöz hasonlóan meghatározhatjuk i_b értékét. Alapegyenleteink a következõek:

u_b = h₁₁ i_b + u_E,

u_E = R_E i_b(h₂₁ + 1).

A bemenõfeszültség és áram hányadosaként megkapjuk a bemenõ ellenállást

$\begin{displaymath}r_{be} = {u_b\over i_b} = h_{11} + (h_{21}+1)R_E\end{displaymath}$

formában. Vegyük észre, hogy most h₁₁ -nél jóval nagyobb értéket is kaphatunk! A vizsgált erõsítõkapcsolásnak két kimenõpontja lehet: jelet vihetünk el az emitterrõl és a kollektorról is. Nagyon érdekes, hogy a feszültségerõsítés az egyik pontra vonatkozóan pozitív, a másikra negatív elõjelû. Ha R_E = R_C, akkor a két kimenõfeszültség azonos nagyságú, közöttük - szinuszos jelekben gondolkodva - 180 fok eltolódás van. 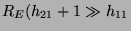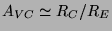(Ezért nevezik ezt az áramkört fázishasító kapcsolásnak is.) Vegyük észre, ha $R_E(h_{21}+1 \gg h_{11}$ , akkor a kollektorra vonatkozó feszültségerõsítés közelítõleg $A_{VC} \simeq R_C /R_E$ nagyságú lesz, vagyis az a paradox helyzet áll elõ, hogy az erõsítés független lesz a tranzisztor paramétereitõl, így áramerõsítésétõl is. Azt is gondolhatnánk, hogy a tranzisztorra nincs is szükség... (A jelenség magyarázatát késõbb, a visszacsatolások ismeretkörében találjuk meg.) Az erõsítõkapcsolás többi jellemzõjét az elõzõ esethez hasonlóan határozhatjuk meg:

$\begin{displaymath}A_{VC} = - {R_C h_{21} \over h_{11}+R_E(h_{21}+1)} \qquad \qq... ...A_{VE} = {h_{21}+1\over r_{be}}R_E \qquad\qquad r_{kiC} = R_C \end{displaymath}$

$\begin{displaymath}f_a = {1\over 2 \pi C (r_{be}\times R_1 \times R_2)} \qquad \qquad f_f = {1\over 2 \pi r_{ki} C_{sz}}\end{displaymath}$

Következõ : Emitterkövetõ, közös kollektorú erõsítõ | Tartalomjegyzék | Elõzõ : Közös emitterû erõsítõ

1999-09-23