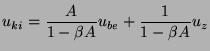

Következő : Impedancia-változások
| Tartalomjegyzék
| Elözö : Második fejezet : Bevezetés
A 2.1.1. ábra azt a legegyszerűbb esetet mutatja, amikor egy
erősítő kimenőjelének 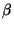 -szorosát visszavezetjük és a bemenőjelhez
előjelesen hozzáadjuk.
-szorosát visszavezetjük és a bemenőjelhez
előjelesen hozzáadjuk. 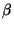 általában kisebb mint egy, mivel nagyon
sokszor ez a hálózat egy egyszerű ellenállás-osztó. Eléggé érdekes
eset, amikor egységnyi: ilyenkor a teljes kimenőjelet visszavezetjük és
a bemenőjel és a kimenőjel közötti különbség vezérli az erősítőt.
A visszacsatolás hatására az erősítő bemenetére jutó ún. vezérlőjel
vagy nagyobb, vagy kisebb lesz, mint visszacsatolás nélkül lenne. Az
előző esetet nevezzük pozitív visszacsatolásnak, az utóbbit negatívnak.
(Az előjel függ tehát az erősítő fázisfordításától; a kis körrel jelzett
összegezőtől, amely esetleg különbségképző; a
általában kisebb mint egy, mivel nagyon
sokszor ez a hálózat egy egyszerű ellenállás-osztó. Eléggé érdekes
eset, amikor egységnyi: ilyenkor a teljes kimenőjelet visszavezetjük és
a bemenőjel és a kimenőjel közötti különbség vezérli az erősítőt.
A visszacsatolás hatására az erősítő bemenetére jutó ún. vezérlőjel
vagy nagyobb, vagy kisebb lesz, mint visszacsatolás nélkül lenne. Az
előző esetet nevezzük pozitív visszacsatolásnak, az utóbbit negatívnak.
(Az előjel függ tehát az erősítő fázisfordításától; a kis körrel jelzett
összegezőtől, amely esetleg különbségképző; a 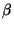 hálózat előjelétol
stb.)
hálózat előjelétol
stb.)
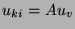
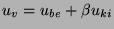
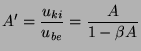
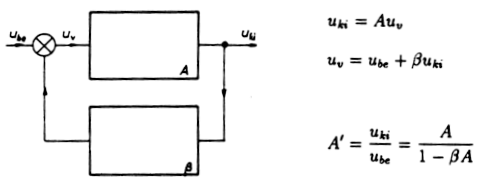
2.1.1. ábra
Viszonylag egyszerűen kaphatjuk meg a visszacsatolt erősítőre
vonatkozó erősítés nagyságát. Különböztessük meg a pozitív és negatív
visszacsatolásra vonatkozó összefüggéseket:
VISSZACSATOLÁS
pozitív:
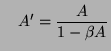 negatív:
negatív:
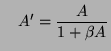
A pozitív visszacsatolásra vonatkozó képlet "veszélyes" - a nevező
lehet zérus, és eredményül végtelen nagy erősítést kapunk. Ezzel a
látszólagos furcsasággal később, az oszcillátorok kapcsán foglalkozunk
részletesebben.
A negatív visszacsatolás mindig csökkenti az eredeti erősítés
nagyságát. Ezt a csökkenést azonban érdemes tudomásul vennünk,
elfogadnunk. Ugyanis:
így a visszacsatolás hatására a eredeti erősítő változásai (pl. a
hőmérséklet, vagy tápfeszültség hatására) relatíve sokkal kisebb
mértékben érvényesülnek. Sot azt látjuk, hogy ha
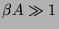 ,
akkor az
erősítést lényegében
,
akkor az
erősítést lényegében  értékével szabhatjuk meg. Ez annyit jelent,
hogy nagyon különböző áramerősítésű tranzisztorokból is lehet mondjuk
tömeggyártás esetén egészen egyforma erősítésű rendszereket készíteni.
Ezt a "trükköt" a biológia is eléggé kiaknázza....
(Két érdekes példát már láttunk. Az emitterkövető
feszültségerősítése azért lesz közel egységnyi, mivel a teljes kimeneti
feszültséget kivonjuk a bemenő feszültségből. Az emitterellenállást
tartalmazó erősítő erősítése pedig azért lesz látszólag független a
tranzisztor paraméterektől, mivel "elfeledkeztünk" arról, hogy ez csak
akkor igaz, ha a rendszer
értékével szabhatjuk meg. Ez annyit jelent,
hogy nagyon különböző áramerősítésű tranzisztorokból is lehet mondjuk
tömeggyártás esetén egészen egyforma erősítésű rendszereket készíteni.
Ezt a "trükköt" a biológia is eléggé kiaknázza....
(Két érdekes példát már láttunk. Az emitterkövető
feszültségerősítése azért lesz közel egységnyi, mivel a teljes kimeneti
feszültséget kivonjuk a bemenő feszültségből. Az emitterellenállást
tartalmazó erősítő erősítése pedig azért lesz látszólag független a
tranzisztor paraméterektől, mivel "elfeledkeztünk" arról, hogy ez csak
akkor igaz, ha a rendszer  erősítése jóval nagyobb egynél, ami persze
tranzisztor nélkül nem állhat fenn....)
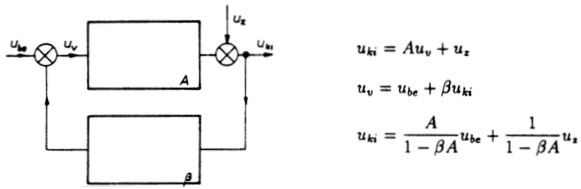
Érdekes jeleségre világít rá a 2.1.2. ábra. Itt azt látjuk, hogy az
erősítő kimeneténél egy újabb jel érkezik a rendszerbe, ezt értelmezzük
zavarjelnek.
Ez a zavarjel különböző okokból állhat elő. Lehet, hogy a hálózati
50 Hz-es jelek tökéletlen egyenirányításából és szűréséből származó ún.
"hálózati brumm". Az is előfordulhat, hogy a kimenőfokozatban a
végerősítő tranzisztor már korántsem tekinthető lineáris
karakterisztikájúnak és így az eredeti jel mellett annak
felharmonikusai is megjelennek és e felharmonikusok a zavarjelek; stb.
erősítése jóval nagyobb egynél, ami persze
tranzisztor nélkül nem állhat fenn....)
Érdekes jeleségre világít rá a 2.1.2. ábra. Itt azt látjuk, hogy az
erősítő kimeneténél egy újabb jel érkezik a rendszerbe, ezt értelmezzük
zavarjelnek.
Ez a zavarjel különböző okokból állhat elő. Lehet, hogy a hálózati
50 Hz-es jelek tökéletlen egyenirányításából és szűréséből származó ún.
"hálózati brumm". Az is előfordulhat, hogy a kimenőfokozatban a
végerősítő tranzisztor már korántsem tekinthető lineáris
karakterisztikájúnak és így az eredeti jel mellett annak
felharmonikusai is megjelennek és e felharmonikusok a zavarjelek; stb.
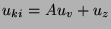
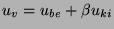
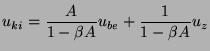
2.1.2. ábra
Jól látszik, hogy zavarjelre vonatkozó erősítés a hasznos jel
erősítéséhez képest igen kicsiny. Azt is mondhatjuk, hogy a zavarjel
ellenkező fázisban kerül vissza a bemenetre, így szinte kioltja
sajátmagát. Ez is jelentős érdeme a negatív visszacsatolásnak.


Következő : Impedancia-változások
| Tartalomjegyzék
| Elözö : Második fejezet : Bevezetés
1999-09-23
![]()
![]()
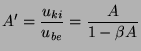

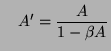 negatív:
negatív:
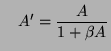
![]()
![]()