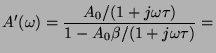
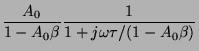
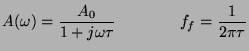
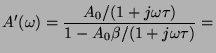
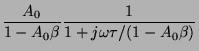

A 2.3.1. ábra azt sugallja, hogy a vizsgált erősítő - mint igen
gyakran - egyetlen felső sávkorlátozó elemet tartalmaz. Ez az
![]() összefüggésbol látszik: a frekvenciakarakterisztika megegyezik az RC
aluláteresztő szűrő frekvenciakarakterisztikájával. Az immáron
frekvenciafüggő erősítéssel elvégezve megszokott számításainkat,
érdekes eredményre jutunk. A negatív visszacsatolás az erősítő felső
frekvenciahatárát növeli, méghozzá olyan mértékben, ahogy az erősítés
csökken. Úgy tűnik, hogy az erősítés-sávszélesség szorzat a negatív
visszacsatolás során nem változik.
Az egész jelenség azonban gondosabb vizsgálatot igényel. Eddig
állandóan követett bennünket az
összefüggésbol látszik: a frekvenciakarakterisztika megegyezik az RC
aluláteresztő szűrő frekvenciakarakterisztikájával. Az immáron
frekvenciafüggő erősítéssel elvégezve megszokott számításainkat,
érdekes eredményre jutunk. A negatív visszacsatolás az erősítő felső
frekvenciahatárát növeli, méghozzá olyan mértékben, ahogy az erősítés
csökken. Úgy tűnik, hogy az erősítés-sávszélesség szorzat a negatív
visszacsatolás során nem változik.
Az egész jelenség azonban gondosabb vizsgálatot igényel. Eddig
állandóan követett bennünket az ![]() mennyiség, összefüggéseinkben
folyton visszatért. E mennyiséget hurokerősítésnek nevezik -- eléggé
szemléletesen, mert ha a visszacsatoló hurkot bárhol felvágjuk, jelet
adunk be és mérjük a visszajövő mennyiséget, mindig ugyanazt az értéket
kapjuk.
mennyiség, összefüggéseinkben
folyton visszatért. E mennyiséget hurokerősítésnek nevezik -- eléggé
szemléletesen, mert ha a visszacsatoló hurkot bárhol felvágjuk, jelet
adunk be és mérjük a visszajövő mennyiséget, mindig ugyanazt az értéket
kapjuk.
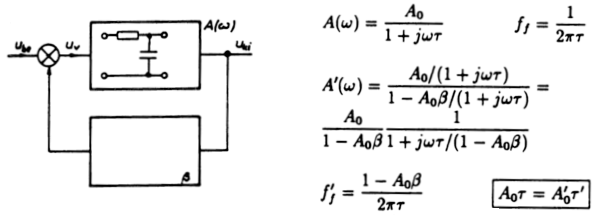
![]() tehát frekvenciafüggő komplex mennyiség, ábrázoljuk ezt
polárkoordináta rendszerben. A 2.3.2. ábra három, egyforma felépítésű
tranzisztoros erősítő fokozatot mutat. A rendszer magasabb
frekvenciákon, ahol a kondenzátorok hatása elhanyagolható, fázist
fordít. Zérus frekvencián pedig átvitele megszűn&ik, de közben
tehát frekvenciafüggő komplex mennyiség, ábrázoljuk ezt
polárkoordináta rendszerben. A 2.3.2. ábra három, egyforma felépítésű
tranzisztoros erősítő fokozatot mutat. A rendszer magasabb
frekvenciákon, ahol a kondenzátorok hatása elhanyagolható, fázist
fordít. Zérus frekvencián pedig átvitele megszűn&ik, de közben
![]() fok fázisváltozás következik be. Ha a magasfrekvenciákért felelős
párhuzamos kondenzátorokat is feltüntettük volna, ezeket hatását is
ábrázolhatnánk a választott koordinátarendszerben.
fok fázisváltozás következik be. Ha a magasfrekvenciákért felelős
párhuzamos kondenzátorokat is feltüntettük volna, ezeket hatását is
ábrázolhatnánk a választott koordinátarendszerben.
A Nyquist-tól származó igen nevezetes eljárás szerint egy
visszacsatolt rendszer stabilitásának vizsgálatát azzal kell kezdenünk,
hogy elkészítjük az áramkörre vonatkozó ![]() hurokerősítéshez tartozó
polárkoordináta diagramot a mínusz végtelen - plusz végtelen
frekvenciasávra. (Így garantáltan mindig zárt görbéhez jutunk. Negatív
frekvenciáknál a képzetes rész előjelét változtassuk ellenkezőjére.)
Ha az ún. Nyquist diagram szerinti zárt görbe magába foglalja az
1,0 pontot, akkor a rendszer nem stabil, hanem oszcillálni kezd. (Az
"1" a képletekben állandóan megjelenő
hurokerősítéshez tartozó
polárkoordináta diagramot a mínusz végtelen - plusz végtelen
frekvenciasávra. (Így garantáltan mindig zárt görbéhez jutunk. Negatív
frekvenciáknál a képzetes rész előjelét változtassuk ellenkezőjére.)
Ha az ún. Nyquist diagram szerinti zárt görbe magába foglalja az
1,0 pontot, akkor a rendszer nem stabil, hanem oszcillálni kezd. (Az
"1" a képletekben állandóan megjelenő ![]() kifejezés egyese.)
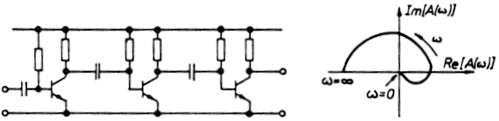
Példákat a 2.3.3. ábrán láthatunk. A görbék mögött nincs valóságos
hálózat, csak az illusztáció kedvéért ilyen furcsák. Az egyik görbe
stabil, a másik oszcilláló rendszerhez tartozik. (A Nyquist féle
stabilitásvizsgálat alaptételét mint eléggé triviálist elfogadjuk. Nem
bizonyítjuk, mert ez nagyobb kitérőt jelentene.)
kifejezés egyese.)
Példákat a 2.3.3. ábrán láthatunk. A görbék mögött nincs valóságos
hálózat, csak az illusztáció kedvéért ilyen furcsák. Az egyik görbe
stabil, a másik oszcilláló rendszerhez tartozik. (A Nyquist féle
stabilitásvizsgálat alaptételét mint eléggé triviálist elfogadjuk. Nem
bizonyítjuk, mert ez nagyobb kitérőt jelentene.)
Kiegészítésként meg kell jegyezni, hogy a stabil/oszcillál kérdés
eldöntése kissé bonyolultabb: meg kell számolni, hogy a görbe az 1,0
ponttól jobbra felfelé és lefelé menet hányszor metszi az X tengelyt,
ha ezek száma különbözik, a rendszer oszcillál.
A Nyquist-től származó módszer igen hatékony, ma is sokszor
alkalmazzák, bár számos vetélytársa létezik. Összetett, többhurkú
rendszereket alapos, előzetes stabilitásvizsgálat nélkül tervezni
lehetetlen.- A hurokerősítés görbe automatizált felvételére bonyolult,
de gyorsan működő cél-műszereket, ún. hálózat analizátorokat
állítottak elő.