Következõ : Frekvenciakarakterisztika kompenzálás | Tartalomjegyzék | Elõzõ : A mûveleti erõsítõk belsõ

Mûveleti erõsítõk a gyakorlatban

Elsõként azt nézzük meg, hogyan lehet általunk kívánt, tetszõleges feszültségerõsítésû rendszert készíteni mûveleti erõsítõvel. A 3.2.1. ábra a legkézenfekvõbb esetet mutatja: pozitív (fázist nem fordító) erõsítõt a negatív visszacsatolás iskolapéldájaként hozhatunk létre. Ha a kimenetet teljesen visszavezetjük a bemenetre, akkor az emitterkövetõhöz hasonló tulajdonságú rendszerhez jutunk.

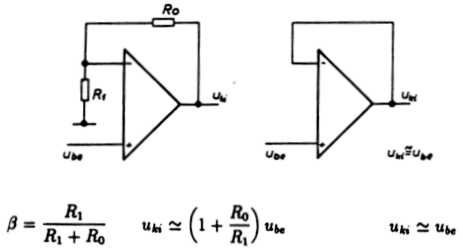
$\begin{displaymath}\beta = {R_1\over R_1+R_0}\qquad u_{ki}\simeq \left(1+{R_0\over R_1}\right)u_{be} \qquad \qquad\qquad u_{ki}\simeq u_{be}\end{displaymath}$

3.2.1. ábra

Negatív erõsítésû rendszert a 3.2.2. ábra szerinti elrendezésben kapunk. Az erõsítés - lényegében - csak a két ellenállás viszonyától függ, ahogy azt a magyarázó ábrákon nyomon követhetjük. A középsõ ábra a kapcsolás lényegét mutatja: az u_v vezérlõfeszültséget a bemeneti és kimeneti feszültség együttesen szabják meg:

$\begin{displaymath}u_v = u_{be}{R_0\over R_1+R_0} + u_{ki} {R_1\over R_1+R_0},\end{displaymath}$

$\begin{displaymath}u_{ki} = u_{be}{R_0\over (R_1+R_0)/A - R_1} \simeq -{R_0\over R_1} u_{be}.\end{displaymath}$

A két ellenállás találkozási pontját virtuális földpontnak nevezik, mivel ha az erõsítõ erõsítése nagy, akkor ezen a ponton szinte nincsen vezérlõjel.

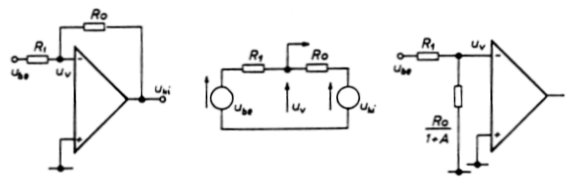
3.2.2. ábra

A kapcsolás mûködését úgy is megérthetjük, hogy az ábra jobb oldalán mutatott megoldással az R₀ ellenállást a Miller-effektusról tanultak értelmében a bemenettel párhuzamos ellenállássá transzformáljuk. Ezután számítjuk ki az immár triviális hálózat erõsítését:

$\begin{displaymath}u_v = {R_0\over R_0+R_1(1+A)}u_{be}\qquad \longrightarrow \qquad u_{ki}\simeq -{R_0\over R_1} u_{be}.\end{displaymath}$

Az (u_kiR₁+ u_be R₀)=0 összefüggés az áramkör egykori kitalálóit a mechanikai nyomaték-egyenletekre emlékeztették, ezért az áramkört "hinta kapcsolásnak" is nevezik. Vegyük észre, hogy a pozitív erõsítésû rendszer bemeneti ellenállása a mûveleti erõsítõ bemeneti ellenállásával egyezik meg, tehát igen nagy is lehet. A negatív erõsítésû rendszer bemeneti ellenállása pedig lényegében R₁ nagyságú. A 3.2.3. ábra-sorozaton számos, nagy gyakorlati értékû kapcsolást látunk. Az áramkörök mellett egyes esetekben feltüntettük az áramkörhöz tartozó legfontosabb összefüggéseket is.

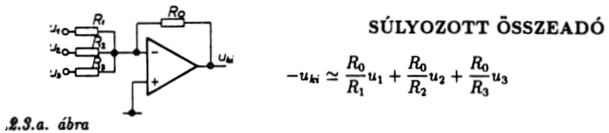
3.2.3. ábra
A súlyozott összeadó feszültségforrások jelének tetszõleges, ellenállásokkal beállítható arányú összegezését végzi. Mûködése a virtuális földpont fogalmán alapul. A következõ ábra két feszültség különbségének elõállításához ad útmutatást. (A képleteket érdemes ellenõrizni.)

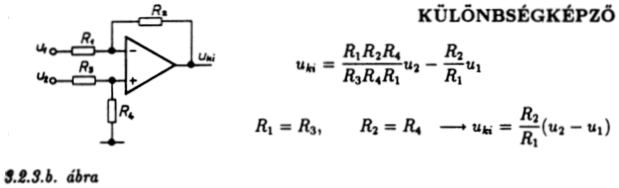
3.2.3b. ábra Az áramgenerátor az R₁ ellenálláson figyelt feszültség visszacsatolásán alapul.

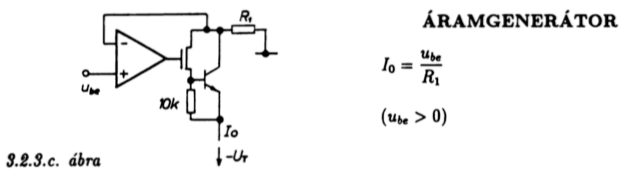
3.2.3.c ábra Az integráló és differenciáló kapcsolások lényegében a Miller-effektusként megismert jelenség alkalmazásai. INTEGRÁLÓ DIFFERENCIÁLÓ

$\begin{displaymath}u_{ki} \simeq - {1\over RC} \int _0^t u_{be}dt \qquad \qquad \qquad \qquad u_{ki} \simeq -RC {du_{be} \over dt}\end{displaymath}$

3.2.3.d. ábra 3.2.3.e. ábra

Megértésükhöz a 3.2.3.f. ábrára utalunk. Itt a bemeneti feszültséget egy ellenállásból és egy kondenzátorból álló rendszerre vezetjük.

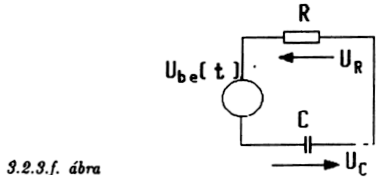
3.2.3.f ábra Ha a kondenzátoron létrejövõ feszültség a bemeneti feszültséghez képest kicsi, akkor az ellenálláson a bemeneti feszültséggel arányos áram folyik át - ezt integrálja a kondenzátor. Ha viszont az ellenálláson a bemeneti feszültséghez képest kicsiny feszültség jön létre, akkor a körben folyó áram a bemeneti feszültség differenciálhányadosa lesz. A Miller-effektus jóvoltából elõálló nagyon nagy kondenzátor nyilván jól integrál, a nagyon kicsiny ellenállás pedig nem zavarja meg a differenciáló kapcsolás kondenzátorának áramát. Ne felejtsük el: egzakt matematikai értelemben egyik kapcsolás sem ad korrekt eredményt, a felírt összefüggések csak közelítõleg igazak, lényegében egy alul- illetve felüláteresztõ kapcsolás tulajdonságait vizsgáltuk. (Az integráló kapcsolásba a 3.2.3.d. ábrán berajzolt telep a kondenzátornak hivatott kezdõ-értéket adni. Amikor a kapcsolót nyitjuk, akkor kezdõdik az integrálás.)

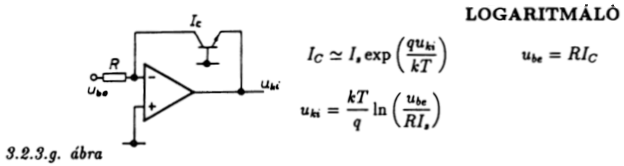
3.2.3.g ábra A logaritmáló kapcsolás lényege: a tranzisztor kollektorárama a bázis-emitter feszültségtõl exponenciálisan függ.

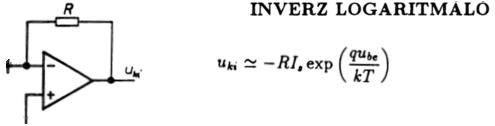
3.2.3.h ábra Hasonlóképpen a dióda exponenciális karakterisztikáját használja ki az inverz logaritmust elõállító kapcsolás. EGYENIRÁNYÍTÓ ABSZOLUT ÉRTÉK KÉPZÕ

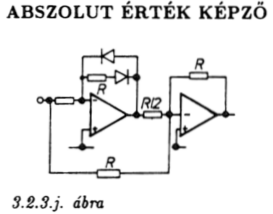
3.2.3.i ábra 3.2.3.j. ábra ??? Az egyenirányító (demoduláló) kapcsolás a különbözõ polaritású jelekhez különbözõ erõsítést rendel. Az egyik polaritásra az erõsítés közelítõleg egy, a másikra, mivel a dióda az erõsítõ bemenetét és kimenetét összeköti, zérus. Az abszolutérték-képzõ (kétoldalas egyenirányító) az eredeti jelnek, valamint az egyoldalasan egyenirányított jel kétszeresének különbségébõl áll elõ. NÉGYZETGYÖKVONÓ SÁVSZÛRÕ

3.2.3.k. ábra 3.2.3.l. ábra A négyzetgyökvonó áramkör alapja az az általános érvényû felismerés, hogy a visszacsatoló ágban található elem karakterisztikájának inverzét kaphatjuk meg a kapcsolás bemenete és kimenete között. Az ábrán a szorzó áramkör a kimeneti feszültség négyzetével arányos jelet állít elõ, kis eltéréssel ez megegyezik a bemeneti jellel. A mûveleti erõsítõn alapuló szûrõ (ún. aktív szûrõ) csak példaképpen szerepel itt, részleteit nem vizsgáljuk, de megjegyezzük, hogy ez is igen fontos alkalmazási területet jelent. A fentiek alapján nyilvánvaló, hogy áramkör-készletünkkel feszültségekkel, illetve feszültség-idõ függvényekkel igen változatos müveleteket tudunk végezni. Valamikor ennek alapján ún. 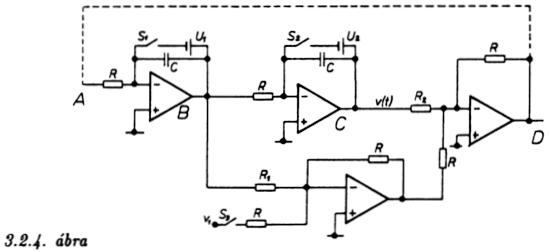analóg számítógépeket is építettek. A 3.2.4. ábra olyan elrendezést mutat, amely egy differenciálegyenlet megoldását szolgáltatja kimeneti feszültségként.

3.2.4. ábra Ha feltesszük, hogy a C ponton v(t) feszültség jön létre, akkor a B és A pontokon kapható jeleket könnyen felírhatjuk:

$\begin{displaymath}{\rm B:} \qquad -RC{dv\over dt} \qquad \qquad \qquad {\rm A:}\qquad (RC)^2 {d^2v\over dt^2}\end{displaymath}$

v₁ figyelembe vételével egyszerûen kiadódik a D ponton megjelenõ jel is:

$\begin{displaymath}-{R\over R_2} v - {R\over R_1}RC{dv\over dt} + v_1 = (RC)^2 {d^2v\over dt^2}\end{displaymath}$

Ha a D és A pontokat összekötjük - mint ahogy a valóságos kapcsolásban össze is vannak kötve, akkor a két feszültség azonosságát biztosítottuk. Az áramkör a felírt differenciálegyenletet realizálja, vagyis a C ponton megkapjuk a v₁ kényszerfüggvény hatására kialakuló v(t) idõfüggvényt. (Ugyanúgy, mintha egy súly-rugó-súrlódás rendszert mozgatnánk valami kényszererõvel és az út-idõ üsszefüggést keresnénk ennek függvényében.) A rendszer mûködéséhez az kell, hogy a t= 0 idõpontban az S₁ és S₂ kapcsolókat nyissuk, amivel a megoldás kezdeti feltételeit állítjuk be, S₃-at pedig zárjuk. Az analóg számítógépek egykori jelentõs&égét digitális társaik elképesztõ fejlõdése alaposan megtépázta. Záró példának tekintsük a 3.2.5. ábrát. Ez az ábrasor egy nagyon fontos alkalmazás "történetét" mondja el több felvonásban. Tegyük fel, hogy van valamely egyenfeszültségünk, amelynek értéke nem állandó, hanem kisebb nagyobb mértékben változik. Ilyet kapunk például a hálózati feszültség egyenirányítása, és szûrése után. Ha ebbõl az 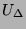$U_\Delta$ feszültségbõl akarunk pl. tranzisztoros áramköreink részére stabil tápfeszültséget nyerni, akkor a triviális megoldás az ábra szerinti emitterkövetõ alkalmazása: a kimenõ feszültség értéke kb. U₀ lesz. A telepet természetesen helyettesíthetjük Zener-diódával - ez már kényelmesebb áramkör. Ha az áramkört lényegi módosítás nélkül átrajzoljuk, akkor jobban látszik, miért nevezik ebben a kapcsolásban a tranzisztort áteresztõ tranzisztornak: ez ereszti a szabályozatlan feszültséget szabályozott formában a terhelésre. Tudjuk, hogy az emitterkövetõ lényegében egy negatívan visszacsatolt rendszer.

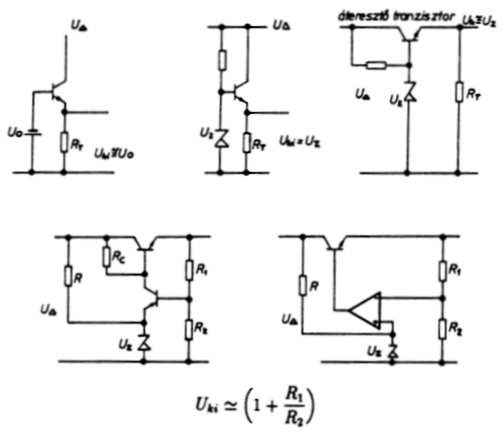
3.2.5. ábra A negatív visszacsatolás hangsúlyozottabb formáját látjuk a következõ ábrán: a kimenõ feszültséget a referenciafeszültség (U_Z) és a kimeneti feszültség leosztott különbsége szabályozza. Ez a kapcsolás nagyon hasznos, gyakran használják. A kimeneti feszültséggel arányos negatív visszacsatolás miatt értelemszerûen igen kicsi a kimeneti ellenállása. (Eddigi terminológiánk szerint ennek az áramkörnek a bemenõ jele a Zener-dióda feszültsége, 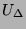$U_\Delta$ pedig a visszacsatolt rendszer zavarjele.) Ilyen stabilizáló kapcsolásokat ma már szinte mindig integrált áramkörös kivitelben használnak. A legtöbb kapcsolás el van látva ún. rövidzár-védelemmel is. Ha ugyanis a kimenetet rövidrezárjuk, az áteresztõ tranzisztorra igen nagy teljesítmény jut, aminek hatására tönkremegy. Ha a kimeneti áram egy meghatározott értékénél újabb visszacsatolást hozunk létre, mely a kimenõfeszültséget drasztikusan csökkenti, akkor az áramkör a nem éppen ritka tápfeszültség zárlatokat is túléli.

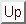
Következõ : Frekvenciakarakterisztika kompenzálás | Tartalomjegyzék | Elõzõ : A mûveleti erõsítõk belsõ

1999-09-23
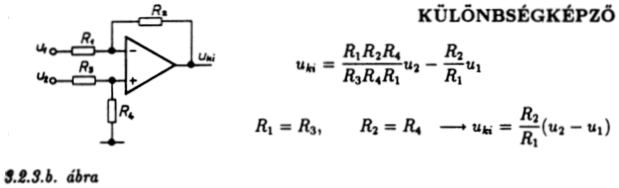
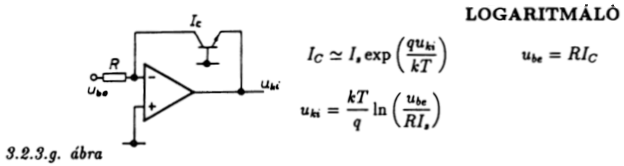
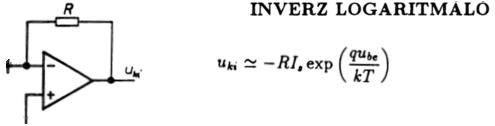