4.2.1. ábra

A háromszoros erősítőt legegyszerűbb egy műveleti erősítő negatív
visszacsatolásával létrehozni. Így jutunk el az ún. Wien-hídas
oszcillátorhoz. (Az elnevezés magyarázata: egy majdnem teljesen
kiegyenlített Wien-híd ici-pici kimenőjelét erősíti a nagy erősítésű
rendszer kimenőjellé, hogy az táplálja a híd bemenetét...) Az áramkör
egy gyakori változatában a negatív visszacsatolási ágban izzólámpát
alkalmaztak. Ennek ellenállása ugyanis a rájutó teljesítmény hatására
növekszik. Ha tehát növekszik a kimenőjel amplitudója, akkor nő a
negatív visszacsatolás mértéke, csökken az erősítés, ami lecsökkenti a
kimenőjel amplitudóját - az izzólámpa tehát egyfajta amplitudó
stabilizálást eredményez. Megjegyezzük, hogy újabban termisztorokkal,
vagy egyéb negatív hőkoefficiensű ellenállásokkal készítik ezt az
áramkört.
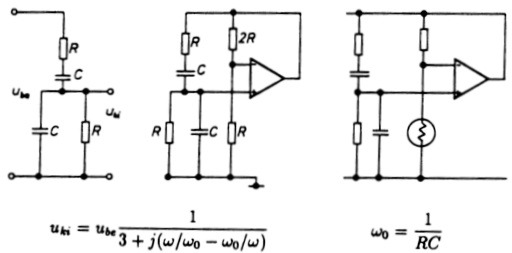
A 4.2.2. ábra az ún. fázistoló oszcillátort mutatja. Az RC
létrahálózat azzal a tulajdonsággal rendelkezik, hogy az ![]() frekvencián
fázist fordít. Ekkor a bemenőjel 1/29-ed része jut a hálózat
kimenetére. Ha tehát egy legalább 29-et erősítő - önmagában is fázist
fordító - erősítő fokozathoz kapcsoljuk, akkor rezgő rendszerhez
jutunk. A kapcsolási elrendezés a komplementer hálózat esetén is
működik, vagyis az R és C elemek kölcsönös cseréje után is.
frekvencián
fázist fordít. Ekkor a bemenőjel 1/29-ed része jut a hálózat
kimenetére. Ha tehát egy legalább 29-et erősítő - önmagában is fázist
fordító - erősítő fokozathoz kapcsoljuk, akkor rezgő rendszerhez
jutunk. A kapcsolási elrendezés a komplementer hálózat esetén is
működik, vagyis az R és C elemek kölcsönös cseréje után is.
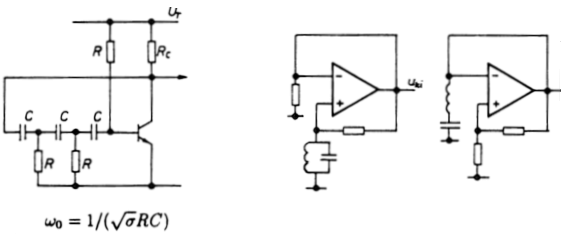
Eddig olyan oszcillátorokat láttunk, amelyek csak RC elemeket
tartalmaztak. Természetesen lehet rezgőköröket is használni frekvencia
megszabó elemként, kihasználva azt, hogy a párhuzamos rezgőkör csak a
rezőnanciafrekvenciáján jelent számottevő ellenállást, illetve azt,
hogy a soros rezgőkör rezőnancia-ellenállása zérus, vagy legalább is
nagyon kicsi. A 4.2.3. ábrán erre látunk példákat. Az első változatnál
a párhuzamos rezgőkör csak a rezőnanciafrekvencián jelent akkora
ellenállást, hogy a pozitív visszacsatolás domináljon. A második
áramkörben a soros rezgőkör rezőnanciafrekvenciáján gyakorlatilag
megszűnik a negatív visszacsatolás, ezért kerül túlsúlyba a pozitív
visszacsatolás.
Külön kell beszélnünk az ún. kvarckristály oszcillátorokról. A
kvarc piezőelektromos tulajdonságú, tehát nyomásra felületén töltések
keletkeznek, illetve megfordítva: elektromos feszültség hatására
mechanikai feszültség jön létre. Egy helyesen megválasztott alakú
kvarclapka tehát mechanikai rezgésekbe kezdhet, ha alkalmas
frekvenciájú jellel gerjesztjük. A mechanikai rezgés frekvenciája
nyilván a kvarc mechanikai tulajdonságaitól, valamint a lapka
geometriai méretétől függ. A kvarc lapka tehát alkalmas lehet egy
oszcilláló rendszer frekvenciájának megszabására.
Elektronikus áramkörök rezgési frekvenciájának beállítására azért
használnak előszeretettel kvarckristályokat, mert ezek rendkívül stabil
- időben állandó értékű, hőmérséklettől alig függő - rezgési frekvenciát
eredményeznek. Stabilitásuk egyszerű kivitel esetén is eléri a 10-5 -
10-6 értéket. (Ennek reciprokát könnyebb értelmezni: 105 -
106
másodperc alatt jelentkezik 1 másodperc hiba akkor, ha ebből órát
csinálunk. Vigyázzunk: ez az adat nem a frekvencia érték pontosságára
utal, hanem csak a frekvencia spontán ingadozására, "lötyögésére". A
frekvenciát lényegében a kristály gyártásakor, a geometriai méretekkel
állítják be. Ez utólag már csak igen kicsiny mértékben szabályozható.)
Ha a kristályt termosztátba helyezik - ma már gyártanak igen kicsike
méretű, elektronikusan szabályozott termosztátokat - akkor elérhető a
10-8 - 10-10 stabilitás érték is, ami ugyancsak lenyugöző eredmény.
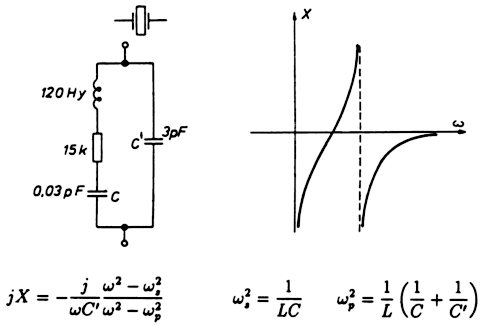
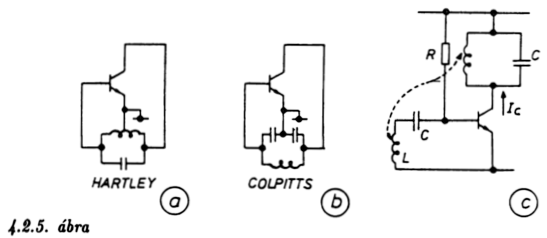
A 4.2.5. ábra c. része egy nagyon gyakran - főként rádió
vevőkészülékekben - használt oszcillátort mutat. A kollektorkörben
elhelyezett rezgőkör induktív csatolással juttat vissza feszültséget a
báziskörbe. Ha ez a "transzformátor" fázist fordít, akkor nyilván
egyetlen tranzisztorral is tudunk oszcillátort készíteni. Ez az
áramkör egy nagyon érdekes tulajdonságot mutat, ami kicsit
részletesebb elemzést igényel, ezért "mikroszkóp" alá helyezzük.
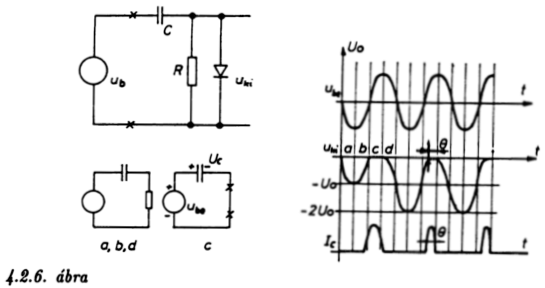
A 4.2.6. ábra az áramkör egy kis részletét mutatja: a
bemenőfeszültség, vagyis az L tekercs végpontjain megjelenő feszültség
egy R-C-dióda áramkörre jut. (Feledkezzünk meg arról hogy a valódi
áramkörben az R ellenállás nem a földponthoz kapcsolódik.) Tegyük fel,
hogy bemenőfeszültségként szinuszos jel érkezik, amelynek amplitudója
"jó nagy". A kimenőfeszültség nyomon követésére a bemenőjel kezdetét
bontsuk szakaszokra.
Az "a" szakaszban a dióda zárt, tehát ha az RC szorzat jóval
nagyobb, mint a periódusidő, akkor a kimenet eléggé pontosan követi a
bemenetet. Ugyanez igaz a "b" szakaszra is.
A "c" szakaszban a dióda kinyit, és ideális dióda esetén a rajta
kialakuló feszültség csak zérus lehet. Ezen szakaszban a kondenzátor
töltődik, feszültsége megegyezik a bejövő feszültséggel. A szakasz
végére a kondenzátor feltöltodik U0 értékre, a bejelölt polaritással.
A "d" szakaszban a dióda újra lezár, és a kimenetet a feltöltött
kondenzátor, valamint a bejövő jel együttesen szabják meg. A
kimeneten kialakuló jelalakot az ábrán láthatjuk.
A kimeneti jelnek jól észrevehető egyenáramú komponense van -
másként kifejezve, a vizsgált elrendezés nevezhető egyenirányítónak,
vagy a későbbiek szerint demodulátornak is. A dióda a periódusidő
túlnyomó részében zárt, nagyon rövid időre kinyit, hogy a kondenzátor
elvesztett töltése ismét pótlódjon. Ha a dióda nyitott, akkor folyik az
eredeti oszcillátor áramkörben kollektoráram. A kollektoráram tehát
csak kicsiny időszakaszokban folyik (![]() fázisszögben), vagyis az
áramkör úgy működik, mint a játszótéri hinta: minden periódusban
rövid ideig kap csak gerjesztő lökést. Ez a kép azt sugallja, hogy
előző megfontolásaink korrekcióra szorulnak: nem igaz az a kép, amely
szerint a tranzisztor (vagy erősítő) lineáris elemnek tekinthető. Ad
absurdum: a tranzisztor a periódusidő túlnyomó részében le van zárva,
akár ki is húzhatnánk és valami hasznosat csinálhatnánk vele egy másik
áramkörben. Az ábra alapos vizsgálatából azt is kideríthetjük, hogy a
bemenő szinuszos jel amplitudójának csökkenésére az áramkör növekvő
fázisszögben), vagyis az
áramkör úgy működik, mint a játszótéri hinta: minden periódusban
rövid ideig kap csak gerjesztő lökést. Ez a kép azt sugallja, hogy
előző megfontolásaink korrekcióra szorulnak: nem igaz az a kép, amely
szerint a tranzisztor (vagy erősítő) lineáris elemnek tekinthető. Ad
absurdum: a tranzisztor a periódusidő túlnyomó részében le van zárva,
akár ki is húzhatnánk és valami hasznosat csinálhatnánk vele egy másik
áramkörben. Az ábra alapos vizsgálatából azt is kideríthetjük, hogy a
bemenő szinuszos jel amplitudójának csökkenésére az áramkör növekvő ![]() folyási szöggel reagál, ami az amplitudó stabilizálását ereményezi.
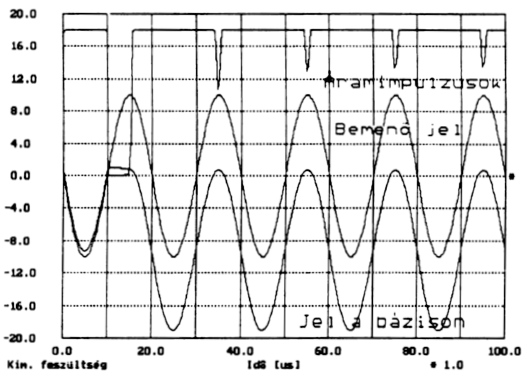
A 4.2.7. ábra a fent leírt áramkörnek és folyamatnak a
számítógépes szimulációját mutatja. Jól látható, hogy - a bekapcsolási
jelenségek lezajlása után - a kollektoráram impulzusok csak a
priódusidő törtrészében folynak.
Az oszcillátorokkal foglalkozó tárgykör befejezéséül egy fontos
fogalommal ismerkedünk, az ún. negatív ellenállásos oszcillátorokkal.
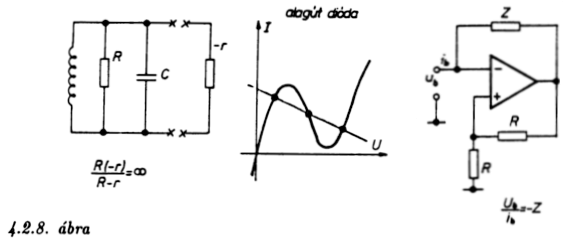
A 4.2.8. ábra alapján egy csillapítatlan rezgést keltő LC
rezgőkörös oszcillátort úgy is felfoghatunk, mintha a rezgőkör
elkerülhetelen veszteségi ellenállásai (huzalok ellenállása,
dielektromos veszteség, sugárzás) mellé párhuzamosan egy azonos értékű
negatív ellenállást helyeznénk. A kérdés csupán az, hogy honnan vegyünk
negatív ellenállást, vagyis olyan elemet, amelyiknek feszültség-áram
karakterisztikájában van olyan szakasz, ahol a feszültség növekedésével
az áram csökken. Ilyen speciális félvezető elemek léteznek: az ún.
alagútdióda is ezek közé tartozik. De negatív ellenállást viszonylag
könnyen létesíthetünk visszacsatolt áramkörökkel is. Erre is látunk
példát az ábra jobb oldalán.
Érdemes belegondolni: olyan elem, kapcsolás, amelyik
karakterisztikája mindenütt negatív, nem létezhet, mert ez korlátlan
energiaforrás lenne. Valós rendszerek csak korlátos szakaszokon
lehetnek negatív ellenállásúak. Az energiát a
tápfeszültségforrásokból nyerik.
folyási szöggel reagál, ami az amplitudó stabilizálását ereményezi.
A 4.2.7. ábra a fent leírt áramkörnek és folyamatnak a
számítógépes szimulációját mutatja. Jól látható, hogy - a bekapcsolási
jelenségek lezajlása után - a kollektoráram impulzusok csak a
priódusidő törtrészében folynak.
Az oszcillátorokkal foglalkozó tárgykör befejezéséül egy fontos
fogalommal ismerkedünk, az ún. negatív ellenállásos oszcillátorokkal.
A 4.2.8. ábra alapján egy csillapítatlan rezgést keltő LC
rezgőkörös oszcillátort úgy is felfoghatunk, mintha a rezgőkör
elkerülhetelen veszteségi ellenállásai (huzalok ellenállása,
dielektromos veszteség, sugárzás) mellé párhuzamosan egy azonos értékű
negatív ellenállást helyeznénk. A kérdés csupán az, hogy honnan vegyünk
negatív ellenállást, vagyis olyan elemet, amelyiknek feszültség-áram
karakterisztikájában van olyan szakasz, ahol a feszültség növekedésével
az áram csökken. Ilyen speciális félvezető elemek léteznek: az ún.
alagútdióda is ezek közé tartozik. De negatív ellenállást viszonylag
könnyen létesíthetünk visszacsatolt áramkörökkel is. Erre is látunk
példát az ábra jobb oldalán.
Érdemes belegondolni: olyan elem, kapcsolás, amelyik
karakterisztikája mindenütt negatív, nem létezhet, mert ez korlátlan
energiaforrás lenne. Valós rendszerek csak korlátos szakaszokon
lehetnek negatív ellenállásúak. Az energiát a
tápfeszültségforrásokból nyerik.