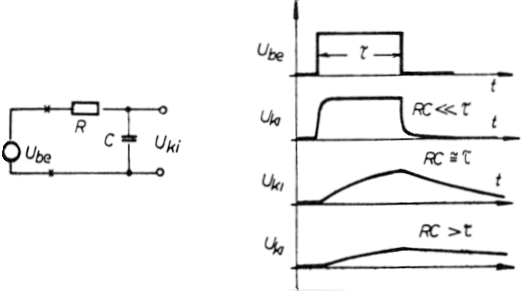
5.2.6/7. ábra

A torzítatlan impulzusátvitel feltétele jelen esetben
![]() ,
ha
pedig
,
ha
pedig ![]() ,
akkor az előzőkhöz hasonló, de most kvázi-integrálásnak
nevezhető folyamat játszódik le. Láthatjuk, hogy az integrálás is csak
hozzávetőleges: az impulzus megszünte után a kondenzátor az időállandó
által megszabott sebességgel elveszti töltését, nem marad azon az
értéken, ahová az "integrálás" alatt feltöltődött.
Összefoglalva megállapítható, hogy mind a differenciáló, mind az
integráló tagok kimenetére eltorzított impulzus jelalakok érkeznek. A
differenciáló tagok elsősorban a tetőesésért, az integráló tagok pedig
az élek "legömbölyödéséért" felelősek. Ez utóbbi nyilván az integráló
tag aluláteresztő jellegének következménye: a kimeneten a gyors
jelkomponensek nem jelennek meg.
,
akkor az előzőkhöz hasonló, de most kvázi-integrálásnak
nevezhető folyamat játszódik le. Láthatjuk, hogy az integrálás is csak
hozzávetőleges: az impulzus megszünte után a kondenzátor az időállandó
által megszabott sebességgel elveszti töltését, nem marad azon az
értéken, ahová az "integrálás" alatt feltöltődött.
Összefoglalva megállapítható, hogy mind a differenciáló, mind az
integráló tagok kimenetére eltorzított impulzus jelalakok érkeznek. A
differenciáló tagok elsősorban a tetőesésért, az integráló tagok pedig
az élek "legömbölyödéséért" felelősek. Ez utóbbi nyilván az integráló
tag aluláteresztő jellegének következménye: a kimeneten a gyors
jelkomponensek nem jelennek meg.