Következõ: Kérdésekfeladatok Fel: Lineáris rendszerek jellemzõi és vizsgálatuk Elõzõ Az egységimpulzus: univerzális vizsgálójel
Következõ: Kérdésekfeladatok
Fel: Lineáris
rendszerek jellemzõi és vizsgálatuk Elõzõ
Az egységimpulzus:
univerzális vizsgálójel
Mielõtt a címben jelzett tárgyhoz hozzákezdenénk, egy a hálózatokkal kapcsolatos fontos fogalmat, a hálózatok idõkésleltetését és annak hatását kell megvizsgálnunk.
Az 11 ábra már ismert jelenségre utal. Ha egy szimmetrikus négyszögjel elsõ és harmadik harmonikusát összegezzük, akkor az eredeti jelhez eléggé hasonló eredményhez juthatunk. Ha azonban a harmadik harmonikus fázisát megfordítjuk, akkor az összeg már nem adja a helyes ábrát.
Ha ennek okát keressük, akkor elõször azt kell
megállapítanunk, hogy mi a hálózatok torzítatlan
jelátvitelének (egyik) feltétele. A Fourier komponensekre
bontás szellemében a bemenetre érkezõ különbözõ
frekvenciájú összetevõk megérkeznek ugyan
a kimenetre, azonban mindegyik némileg késik. Ha a bemeneten
a jelkomponensek egymáshoz viszonyított fázisa adott,
akkor az alakhû átvitel feltétele, hogy a kimeneten
is ugyanilyen legyen a viszonyuk. A kimeneten megjelenõ (szinuszos)
jelek 
formában írhatók fel. 
azt fejezi ki, hogy a különbözõ frekvenciákhoz
különbözõ késleltetési idõ tartozhat.
Kézenfekvõ, ha
a frekvenciától független állandó 
,
akkor a komponensek fázisviszonyai a kimeneten éppen olyanok
lesznek, mint a bemeneten. Vizsgáljunk most egy egyszerû példát,
az RC aluláteresztõ szûrõt. Ennek fázistolása
A kimenet és bemenet közötti idõkésés mértéke - állandósult szinuszos jelet feltételezve - könnyen meghatározható.
Jól látszik, hogy a késleltetés akkor lesz
állandó, ha 
függvény lineáris, vagyis 
. Az RC aluláteresztõ esetében más a helyzet,
mint ahogy az áramkörök többségében
is.
Az 12 ábra baloldalán az
RC aluláteresztõ fázis és késleltetési
idõ görbéi láthatók. Feltüntettük
a 
ún. csoport-futási idõ görbét is. Ezt
szokták a hálózat "diszperziójának"
tekinteni, amely fogalom arra utal, hogy a különbözõ
frekvenciájú komponensek mennyire "szóródnak
szét" egymáshoz képest a hálózaton
való áthaladásukkor (v.ö. kísérleti
fizika fázisebesség). Az ábra jobb oldalán
az ideális aluláteresztõ hálózat abszolútérték
átvitelét és fázismenetét ábrázoltuk.
Ez az ábra egyúttal e fogalom definíciójaként
is tekinthetõ.
Eléggé magától értetõdõnek
tûnik azt kérdezni, hogy milyen kimenõjelet kapunk,
ha egy ideális aluláteresztõ szûrõ bemenetére
ideális impulzust adunk. Ha az impulzus nagysága (amplitúdó-idõtartam
szorzat) egységnyi, akkor a kimeneten megjelenõ komponens
értékû lesz. A Fourier (vissza ) transzformálás
szabályai szerint (itt az 
kifejezés a minden frekvenciáára azonos mértékû
jelkésleltetésre utal):
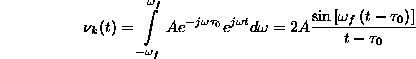
Az eredménybõl az alábbi fontosabb tanulságok vonhatók le:
alakú lesz, - a Fourier transzformáció során
tehát az idõbeni és frekvenciatartománybeli
jelalakok ``felcserélhetõk'', szimmetrikusak; 
összefüggésbõl 
értékûre adódik. A kimenõjel "fõhulláma"
tehát ennyi ideig tart, vagyis az aluláteresztõ felsõ
határfrekvenciájának a reciproka szabja meg. Ez nagyjából
megegyezik régebbi ismereteinkkel, amelyeket pl. a kváziintegráló
áramkör kimenetén kapható legrövidebb impulzusról
szereztünk. - A dolog elvi jelentõsége nagyon fontos:
a felsõ frekvenciahatár szabja meg a kimeneten kialakuló
legrövidebb impulzus szélességét. 
sávszélességû rendszeren legfeljebb 
jel (impulzus) vihetõ át megkülönböztethetõen.
Az 14 ábra a. része különös
(ideális) impulzussorozatot mutat. A jelenség periodikus,
azonban bizonyos idõpontokban nem jelenik meg az impulzus. Ez így
egyszerû modellje a bináris információ közlésnek:
az "1" esetben van impulzus, "0" esetben nincs. Ezek
a jelek - feltevésünk szerint - egy ideális aluláteresztõn
haladnak keresztül. Mindegyik bemeneti impulzus a kimeneten
alakú jelet kelt. Ezek természetesen a bemeneti impulzushoz
képest késve jellenek meg a kimeneten. A b. ábrán
ezt a késleltetést a valóságos fizikai esettõl
eltekintve zérusnak tekintjük, hogy az ábrasor áttekinthetõ
legyen. A kimeneten 
alakú jelek összege jelenik meg. Nagyon fontos tudatosítani,
hogy ez az összeg - a mintavételi idõpontoktól
eltekintve (c. ábra) - nem korlátos, mert az 1/k szerint
csökkenõ mellékhurkok összege bármilyen
értéket felvehet. - Ha a mintavételi idõpontokat
egybeejtjük az eredeti impulzusok idõpontjaival, akkor a mintavételi
idõpontokban az esetleg véletlenszerûen változó
múltbeli impulzusok esetén is pontosan kaphatjuk a kérdéses
impulzus amplitúdóját. - Az elõbb már
láttuk a
alakú jelek részletesebb vizsgálatánál,
hogy a helyesen detektálható jelek ismétlõdési
idejének 
-nek kell lennie. Az ábra c. része a mintavevõ jeleket
tünteti fel, d. részén pedig a detektált kimenetet
látjuk. A fenti gondolatsor persze nem bizonyítás,
csupán értelmezése a Nyquist tételnek. Ez a
tétel az információközlésnek sarkalatos
törvénye: véges felsõ határfrekvenciájú
rendszeren nem lehet a határfrekvencia kétszeresénél
gyorsabban impulzusokat (vagyis a lehetõ legrövidebb jeleket)
továbbítani. (Ezt hívják Nyquist sebességnek.)
Vegyük észre azt is, ha a bemeneti impulzusok amplitúdói
különbözõ nagyságúak lehetnek, ezek
magasságával is közölhetünk információt.
Az ismertetett mintavételi eljárás ezeket is pontosan
adja vissza, vagyis az átvitt információ mennyisége
így is növelhetõ. Ennek a módszernek az átviteli
csatornák zaja jelenti a korlátját, emiatt a a detektált
impulzus amplitúdók nem lesznek egyértelmûen
megkülönböztethetõk. - Ezzel eljutottunk a csatornakapacitás
fogalmához, amely egy
felsõ frekvenciahatárú csatornán átvihetõ
maximális információfluxust adja meg, vagyis a másodpercenként
átküldhetõ ideális impulzusok számát:
A delta-impulzus hálózaton történõ
átvitelének ismeretében más, technikai szempontból
értékes ismerethez is könnyen juthatunk. Igy pl. meghatározhatjuk,
hogy ugrásjel (lépcsõ- függvény) hatására
mi jelenik meg az ideális aluláteresztõ kimenetén.
Ehhez azt kell észrevennünk, hogy a kimeneti jel frekvenciaspektruma
mindig a bemeneti jel és a hálózat frekvenciaspektrumának
szorzataként áll elõ. Ha a bemeneti jelet differenciáljuk,
ez a bemenõjel spektrumának 
-val történõ szorzásával, vagy osztásával
egyenértékû. Ilyenkor azonban nem választható
szét, hogy a mûveletet a bemeneti jelen, vagy a kimeneten
hajtottuk végre.
A dolog lényege: a bemenõjel differenciálásával , vagy integrálásával elõálló bemenõ jelalakhoz tartozó kimenõjelet a kimenõjel differenciálásával, illetve integrálásával is kaphatjuk. (Persze fordítva is !)
Adjunk például egy ideális aluláteresztõ
szûrõ bemenetére feszültségugrást.
Ez az impulzus függvény integrálja, - tehát a
kimeneti jelet megkaphatjuk az impulzushoz tartozó kimenõjel
integrálásával (15 ábra).
Az ugrásfeszültség hatására tehát
a
függvény integrálja fog a kimeneten megjelenni. (Természetesen
itt is sérül az oksági elv.)
