Következõ: Dekonvolúció Fel: Lineáris rendszerek jellemzõi és vizsgálatuk Elõzõ Kérdésekfeladatok

Konvolúció

Ennek a tantárgynak az egyik legérdekesebb részéhez értünk el. Itt a szuperpozíció elvét fogjuk kihasználni a hálózatokra adott jelre adott kimeneti válasz keresésénél.

Állításunk a következõ: lineáris hálózatok esetében a súlyfüggvény ismeretében tetszõleges bemenõjelhez meghatározhatjuk a kimenõjelet. Az 16. ábra ezt részletesen követhetõvé teszi.

  
16. Ábra

Az a. ábra egyetlen bemenõ impulzus sorsát tünteti fel, tehát ennek kimeneti válaszfüggvénye a h(t) függvény. A b. ábra bemenõjele több impulzusból áll, ezek mindegyike kivált egy h(t) függvényt a kimeneten. - A t idõpillanatban létrejövõ jelet az "elõzményekbõl'' összegzéssel határozhatjuk meg.

A c. ábra már egy kicsit más helyzetet mutat. Itt a bemeneti függvény folyamatosan változik. A t1 idõpont közvetlen közelében vett dt1 érték v(t1) értékével együtt egy delta függvényt határoz meg, tehát a kimenet, - az elõzõhöz hasonlóan - a súlyfüggvények által determinált. a v(t) függvény nagyságú elemi impulzusokból tevõdik össze. A kimenõjel általános formulája könnyen felírható. A kimeneten megjelenik a bemeneti impulzus hatására:

nagyságú jel. Ennek szellemében a kimenet:

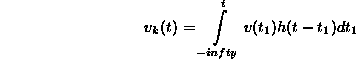
Ez fontos összefüggés, nagyon sok helyen felhasználható. (Számos, módosított alakja is létezik.) - Az integrál által megszabott mûveletet konvolúciónak hívják. Talán most már megérthetõ, hogy ez a szuperpozíció elv leglényegesebb következménye, és nagyon tág az alkalmazási területe.

Példaképpen számoljuk ki egy alsó és felsõ frekvenciahatárral rendelkezõ (vagyis valóságos) erõsítõ kimenetén az ugrásfüggvény hatására a kimeneten keletkezõ jelalakot (4 ábra). - Ez nem csupán gyakorló feladat, hanem fizikusok esetében a nukleáris jelek detektálásának/erõsítésének alapvetõ kérdését is érinti. ( A nukleáris jeldetektorok többsége ugyanis egy - általában a detektált részecske energiájával arányos - feszültségugrást ad az erõsítõ bemenetére.)

 

Az ugrásfüggvény hatására a bemeneti kvázidifferenciáló áramkör kimenetén jellegû függvény keletkezik. Ezt kell konvolválni egy idõállandójú - már az elõzõ részben megismert, kváziintegráló áramkör súlyfüggvényével. A konvolúció integrál felhasználásával az eredmény:

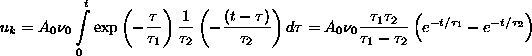
Ez könnyen kiszámolható, - és az eredmény arra utal, hogy a kváziintegráló és a kvázidifferenciáló áramkörök mennyire módosítják a kimeneti jel alakját és amplitúdóját. Az eredmény kvalitatíve az 4 ábrán látható. (A görbék mellett feltüntettük az integráló, majd a differenciáló idõállandó értéket -ban.)

 

Követklezõ: Dekonvolúció Fel: Lineáris rendszerek jellemzõi és vizsgálatuk Elõzõ: Kérdésekfeladatok