Következõ: Integráló voltmérõ Fel: Jelek vizsgálata zaj jelenlétében Elõzõ Jelek vizsgálata zaj jelenlétében

A zajok jellemzõi

A méréstechnika egyik legfontosabb célja: küzdelem a mindig, mindenütt jelenlevõ zaj ellen. A zajok általában nem kívánt, de az általunk éppen vizsgált mennyiséget befolyásoló természeti folyamatok eredményei, így könnyen átlátható, hogy sokfajta zaj létezhet. (A zajok sohasem szüntethetõk meg, szemben a zavarokkal. A zavarok ember-keltette jelek, pl. fénycsövek mûködésétõl származnak. Megszüntetésük, csökkentésük csak elvben lehetséges, a valóságban sokszor lehetetlen.) A zajok csak valószínûségi adatokkal jellemezhetõk, e jellemzõk maguk is valószínûségi változók. Két gyakran használt fogalmat a 69 ábra alapján értelmezünk: fehér zajról akkor beszélünk, ha a zaj energia/teljesítményspektruma egy adott frekvenciatartományban állandó értékû. -- Gauss zajnak azt nevezzük, amikor a zaj pillanatnyi amplitúdó eloszlása a Gauss féle valószínûségeloszlást követi. E két dolog nem szükségképpen jár együtt, de a valóságos zajok, -- pontosabban a matematikai módszerekkel tárgyalható zajok -- többsége ilyen. (Gyakran beszélünk ún. random zajrol is. Itt a pillanatnyi amplitúdó eloszlása egyenletes, állandó értékû. A DSPLAY program a Gauss és random zajok eloszlását könnyen szemléltethetõvé teszi.

Zajok esetében a szokásosan mért mennyiségek (átlagérték, effektívérték, csúcsérték) közül tulajdonképpen csak az effektívértéknek van értelme. Ha egy nagyságú egyenáramú jelre egy szórású Gauss eloszlású zaj szuperponálódik, akkor e jel teljesítménye:

(Ezt az összefüggést csak bizonyos valószínûségszámítási ismeretek birtokában lehet átlátni, értelmezni. )

Ez azt jelenti, hogy -- a várakozásnak megfelelõen -- a jel teljesítménye az egyen- és váltakozóteljesítmények összege. Az azonban nagyon érdekes és értékes eredmény, hogy a zaj effektív értékének méréseként kapott mennyiség (teljesítmény) a szórásnégyzettel egyezik meg esetén. Így tehát egy meglehetõsen összetett valószínûségi adatot viszonylag hétköznapi mûszerrel, vagyis ún. valódi effektívérték mérõvel közvetlenül mérhetünk.

  
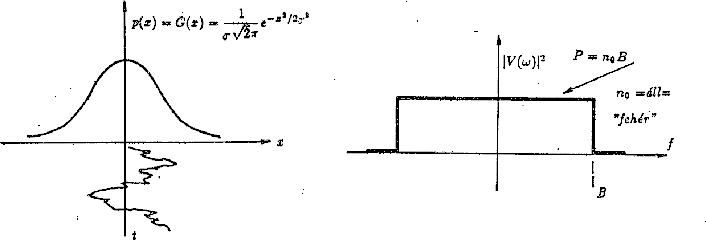
69. Ábra: A Gauss-zaj és a fehérzaj

Ha ismerjük az értékét, vagyis az egy Hz sávszélességre jutó zajteljesítmény nagyságát, akkor a B sávszélességû fehér zaj teljesítménye az alábbi összefüggésbõl számolható: