Következõ: Fõkomponens analízis Fel: Jelek vizsgálata zaj jelenlétében Elõzõ Ismert jelalak amplitudójának mérése

Wiener szûrés

A 1.6 fejezetben láttuk, hogy a dekonvolúció segítségével egy hálózat torzítását egy korrekciós hálózattal kompenzálhatjuk a frekvenciatérben. A módszer alkalmazásának mindenképpen korlátot szabnak a zajok. Érdemes tehát megvizsgálni, hogy zaj jelenlétében hogyan lehet meghatározni az optimális szûrõt.

Legyen , és mérjük a zajos jelet, ahol z(t) a mérés során megjelenõ zajt írja le. Az optimális szûrõ az lesz, amelyik esetén a mért -t megszûrve, majd ezt dekonvolválva a -val az így kapott V a legjobban közelít -hez. Azaz

esetén minimális. Behelyettesítve -t kapjuk, hogy:

Mivel a zaj és a jel korrelálatlan, ezért keresztszorzatuk eltûnik. Ekkor a képlet

alakú lesz. Ez nyilvánvalóan csak akkor lesz minimális, ha minden értékénél minimális. Deriválva szerint megtalálhatjuk a minimumot

Ez lesz az optimális Wiener szûrõ alakja. A szûrõ úgy mûködik, hogy ahol sokkal nagyobb, mint , ott 1 körüli értéket vesz fel, ahol pedig a zaj teljesítménye sokkal nagyobb ott pedig kb. a jel/zaj viszony négyzetével csökkenti a értékeit.

Figyeljük meg, hogy a Wiener szûrõ nem tartalmazza a rendszer súlyfüggvényét, csak a zaj és a jel teljesítményspektrumát. Az optimális szûrõhoz ezért meg kell határozni a zaj teljesítményspektrumát is (nem fehér-zajunk is lehet!). A legegyszerûbb esetben ezt egy helyettesítéssel végezhetjük el. Nagyobb pontosságot már a durva megbecsülésével is könnyen elérhetünk, ui. a Wiener-szûrõ másodrendben tartalmazza -t és Z-t.

  
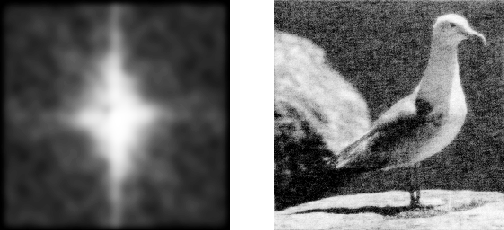
78. Ábra: A kép Fourier-transzformáltja (az egyenszint a kép közepére van eltolva)
79. Ábra: Zajos eredeti kép

  
80. Ábra: A szûrt és visszaalakított kép
81. Ábra: Az alkalmazott Wiener-szûrõ