Következõ: Wiener szûrés Fel: Jelek vizsgálata zaj jelenlétében Elõzõ Kváziperiodikus jelek mérése zaj jelenlétében
Következõ: Wiener
szûrés Fel: Jelek
vizsgálata zaj jelenlétében Elõzõ
Kváziperiodikus
jelek mérése zaj jelenlétében
Egy t szélességû négyszögimpulzus amplitudóját kivánjuk igen széles sávú fehérzaj környezetében megmérni. Mind a zaj, mind a jel egy H ideális aluláteresztõ hálózaton halad keresztül (l. 75 ábra. Vizsgáljuk meg kvalitatíven, hogyan változik az ideális aluláteresztõ kimenetén a jelnek és a zajnak a ngysága. Az ábra jobb oldalán az látszik, hogy H sávszélességének növelésével a kimeneten észlelhetõ jel amplitudója egy határig növekszik, majd gyakorlatilag állandó értékû marad. A kimeneten észlelhetõ zaj H sávszélességének növelésével arányosan nõ. Sejthetõ, hogy létezik egy optimum, amikor a jel már elég nagy, de a zaj még mérsékeltt, vagyis a jel/zaj a legnagyobb értékû. A jel/zaj fogalom igen fontos, számos szakma használja.
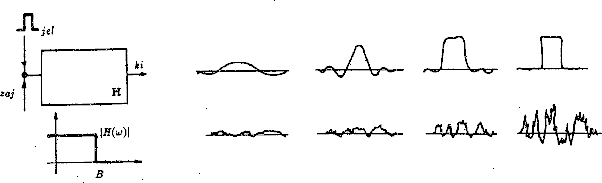
75. Ábra: Az illesztett szûrõ elve
A kérdést általánosabban is fogalmazhatjuk. Ha ismerjük a bemenõjel alakját, hogyan kell a hálózat frekvenciakarakterisztikáját megválasztani, hogy a kimeneten megjelenõ jel maximumából a lehetõ legnagyobb biztonsággal következtethessünk a bemenõjel amplitúdójára?
Keressük az alábbi összefüggés maximumát h(t) függvényében (S/N = Signal/Noise ratio = jel/zaj viszony):
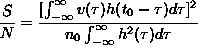
Alaposabb - itt nem részletezett - matematikai elemzés
szerint maximális értéket akkor kapunk, ha 
,
vagyis optimális hálózatválasztás csak
a bemenõjel ismeretében lehetséges. (Az esetleg nekünk
üzenõ kis-zöld-emberkék jeleit tehát semmiképpen
sem tudjuk -- legalábbis kezdetben -- optimális körülmények
között detektálni.) Ha a hálózat a jelhez
ilyetén módon alkalmazkodik, akkor ún. illesztett-szûrõs
jeldetektálásról beszélünk. Természetesen
a hálózat frekvenciakarakterisztikája is pontosan
meghatározható a
feltételbõl.
Illesztett szûrõt LRC elemekbõl nem minden bemenõ jelalakhoz lehet készíteni, példának okáért az exponenciális lefutású triggerjel tükrözött változata fizikailag lehetetlen hálózatot tételez fel. Természetesen digitális szûrõvel ez is megközelíthetõ, tetszõleges pontossággal.
Arra a kérdésre, hogy mennyire érdemes az illesztett
szûrõs optimumra törekedni, a 76
ábráról kaphatunk némi információt.
Ha egy 
szélességû impulzust különbözõ
B sávszélességû aluláteresztõn
küldünk keresztül, akkor a jel/zaj az ideális esethez
képest természetesen rosszabb lesz. A romlás mértékét
az ábráról olvashatjuk le. Az is látható,
hogy az ideális aluláteresztõ szûrõ sokkal
kevésbé érzékeny az impulzus szélességére.
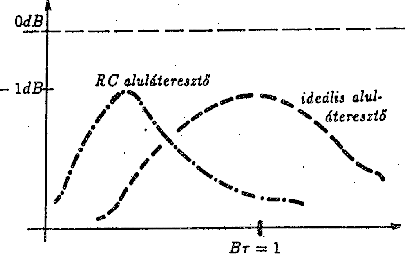
76. Ábra: Illesztett szûrõ optimuma ideális
és RC aluláteresztõ szûrõ esetén
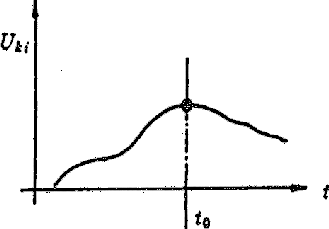
Az illesztett szûrõ fogalmához másfajta gondolkodással is eljuthatunk (77 ábra). Tételezzük fel, hogy a bemenõjel két Dirac-deltából áll, amelyek egymáshoz képesti amplitúdóarányát ismerjük. Keressük azt a hálózatot, amely a két jelet -- zaj jelenlétében -- úgy kombinálja, hogy egyetlen mérésbõl minél pontosabb adatot kapjunk a bemenõjel amplitudójára, A-ra.
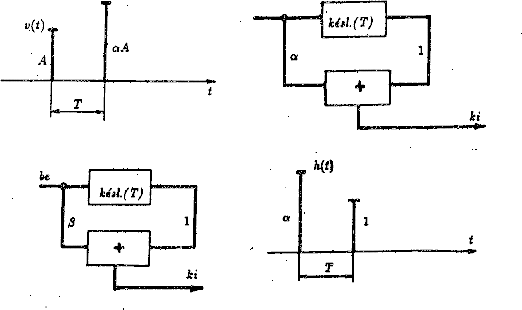
77. Ábra: Két Dirac-deltából álló
jel amplitúdómérésének optimalizálása
illesztett szûrõvel
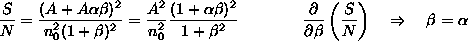
A hálózatként válasszunk egy nagyon egyszerû
digitális (FIR) szûrõt, amelynek egyetlen paramétere
(
)
ismeretlen. A jel/zaj-ra felírt összefüggés szélsõérték
helyének keresése a 
összefüggésre vezet. (Az összefüggés
levezetésénél felhasználtuk azt a tényt,
hogy a kellõképpen késleltetett zajjelek szorzatának
átlagértéke zérus.) A hálózat
súlyfüggvénye tehát a bemenõjel tükörképe
lesz, - amint azt az elõbbi, általánosabb meggondolásból
is láttuk.