Fel: Jelek vizsgálata zaj jelenlétében Elõzõ Wiener szûrés

Fõkomponens analízis

Alkossanak mérési adataink minden idõpillanatban egy n dimenziós vektort. Tekintsük kifejtését egy ortonormális (azaz ) bázis szerint:

, ahol és . Az ortonormalitás miatt igaz lesz, hogy . Látható, hogy egyszerûen egy elforgatottja lesz. A fõkomponens analízisben -t tulajdonságnak nevezzük, egy ilyen tulajdonság értékét az adatokon a komponensek mérik.

Tegyük fel, hogy ki szeretnénk választani m (< n) olyan -t, amelyik -et legjobban közelíti. Ehhez nem használt tagjait (elõre meghatározandó) konstansokkal helyettesítjük:

Minimalizálni akarjuk a eltérés-négyzetet, ekkor (az itt szereplõ E() a várható értéket adja meg):

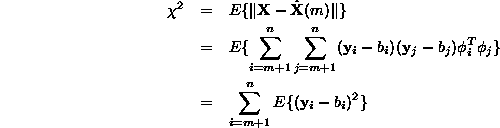
A minimumhoz deriválnunk kell -t szerint. Innen kapjuk, hogy . Ezt visszaírhatjuk -be:

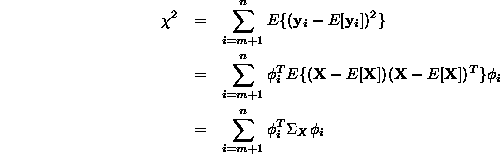
Az itt szereplõ az adatok ún. kovariancia mátrixa. Bebizonyítható, hogy -re az optimális választás a

, azaz a a sajátértékhez tartozó sajátvektor. Így

Azt az eredményt kaptuk tehát, hogy a (a közelítés értelemben) a legjobb lineáris reprezentációt akkor kapjuk, ha a kovariancia mátrix sajátvektorai szerinti ortogonális transzformációt választjuk. Itt célszerû a sajátvektorokat monoton csökkenõ sorba rendezni (azaz az i index szerint , ha i > j. Az eljárás neve is innen ered: ha csak az m (< n) ``fõ'' komponenst választjuk ki, akkor az eltérés az eredeti adatoktól minimális lesz.

A 82 ábrán ez az analízist láthatjuk két dimenzióban. A és sajátvektorok az eloszlás fõ tengelyeit alkotják, miközben a és sajátértékek megmondják a és tengelyek mentén az eloszlás varianciáját. Mivel , ezért és lesznek vetületei a a és tengelyekre.

  
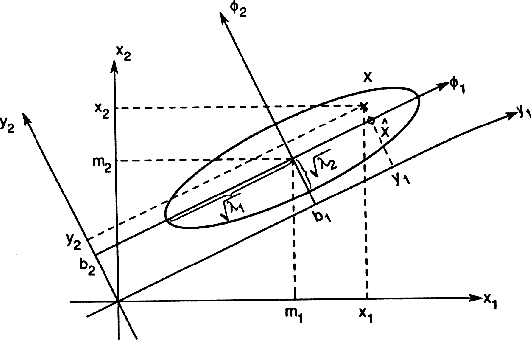
82. Ábra: Példa két dimenzióban a fõkomponens analízisre.

A tulajdonságok több szempontbók is vonzóak: pl. ha töröljük az tulajdonságot, akkor a közelítés hibája -vel nõ meg. Ez lehetõséget biztosít az adatok veszteséges tömörítésére is: amennyiben csak a legnagyobb m sajátkomponenst és az arra vett vetületeket tároljuk, akkor a visszaállítás során az átlagos eltérés értéke lesz. Ha ez sokkal kisebb, mint , és m sokkal kisebb, mint n, akkor jelentõs tömörítést érhetünk így el.

További jó tulajdonság az eljárásnak, hogy az egyes tulajdonságok egymástól függetlenek, azaz az -k egymás közötti korrelációja 0. A fõkomponens analízis az adatok entrópiájára is szélsõértéket biztosít: bebizonyítható, hogy az összes lineáris transzformáció közül ez a transzformáció minimalizálja a transzformációk Y terében mért entrópiamaximumot (minimax viselkedés).

Érdekességként megjegyezzük, hogy stacionárius idõsorok esetén a fõkomponens analízis tulajdonság-függvényei alakúak lesznek, azaz ekkor visszakapjuk a Fourier-transzformációt! Ez talán nem is annyira meglepõ, ha visszagondolunk, hogy a Fourier-transzformációt minimalizálással is bevezethetjük.

A fõkomponens analízis hátrányai között említhetjük, hogy nem mindig (fizikailag) értelmes a mátrix számolásakor levonni az átlagértéket. Természetesen ezt elhagyhatjuk, hiszen helyett bármilyen (nem szinguláris) szimmetrikus mátrixot vehetünk, de ekkor a korábban említett minimalizációs tulajdonság nem lesz igaz. A másik hátrány, hogy az eljárás csak lineáris tulajdonságokat képes megtalálni, pl. egy adott síkban körívet leíró adatoknál nem találja meg (legfeljebb közelíti) az adott ívnek megfelelõ egydimenziós teret. Ezt a hátrányt az adatok normalizálásakor ki is használhatjuk: pl. az adatokat szerint normálva a fõkomponens analízis rendben végrehajtható, míg a normálást használva ezt nem tehetjük meg, mivel szinguláris lesz.

Fel: Jelek vizsgálata zaj jelenlétében Elõzõ: Wiener szûrés