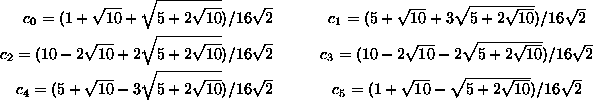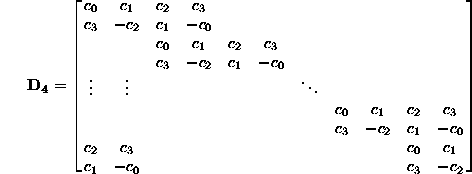
A következőkben a DWT egyik fajtájával, a Daubechies által felfedezett DAUB4 wavelettel foglalkozunk. A transzformáció egy lépését a következő mátrix definiálja (a nem jelzett elemek értéke 0):
Ez a 
mátrix az 
(bemenő)
adatokból állítja elő az 
(kimenő) wavelet transzformáltat. A műveletet érdemes összehasonlítani a
diszkrét Fourier transzformáció
. oldalon látható mátrixalakjával (természetesen ne
feledkezzünk el arról, hogy itt több lépésünk is lesz egymás után).
A hatása a bemenő adatokra a speciális
elrendezés miatt két FIR szűrő hatásaként is is elképzelhető: a
páratlan sorokban a 
együtthatók, mint egy
``simítást'' (integrálást) végző FIR szűrő működnek, míg a páros
sorokban a 
együtthatók deriválják,
``durvítják'' az adatokat, méghozzá úgy, hogy ``elegendően'' sima
bemenő jelre a kimenetük zérus (ezt a két műveletet kvadratúra
tükör szűrőknek is nevezik).
Követeljük meg, hogy konstans és lineáris jelekre a páros sorok végeredménye eltűnjön, valamint azt, hogy a mátrix inverze annak transzponáltja legyen:
A DAUB4-hez hasonlóan a család többi tagja is megkapható, ha a hat, nyolc stb. tagot veszünk, és megköveteljük, hogy másod-, harmad- stb. fokú a bemenő jelre a páros sorok eredménye nulla legyen. A DAUB6 például a következő c-kből áll:
