Következõ: 16.1 A Daubechies waveletek Fel: Digitális jelek feldolgozása Elõzõ Egyéb eljárásokmódszerek

Wavelet transzformáció

A jelfeldolgozás során elõforduló jeleknek eddig vagy az amplitúdó - idõ és az amplitúdó - frekvencia leírását használtuk.

Pl. egy ilyen leírás megadja a mért jel amplitúdójának idõfüggését - a jellemzõ frekvenciákról ilyenkor nem tudunk semmit, azok vizsgálatához át kell térnünk a frekvencia-térbe.

A Fourier transzformációval a frekvencia-térbeli leírás pontosan megadja a jelsorozatot létrehozó sin és cos függvények amplitúdó és fázisértékeit, de semmit nem mond a jel idõbeli változásairól (pl. a jellemzõ idõbeli frekvenciák változásáról).
Erre példa egy rövid, Dirac-delta jellegû impulzus Fourier-transzformáltja: ahogy azt a . fejezetben láttuk ez nagyon sok, kb. ugyanolyan amplitúdójú és hullámból áll. A hullámok fázisai ``pontosan'' úgy állnak, hogy az impulzus elõtt és után a hullámok kioltják egymást, de a megfelelõ idõpontban az impulzus megjelenik: a Fourier-térben nem lehet közvetlenül megmondani az impulzus elõfordulási idejét.

A wavelet transzformált a rögzített, a csak idõ vagy a csak frekvencia kép ``közötti'' leírás. A wavelet transzformáció segítségével a jelek idõbeli (vagy térbeli) és a frekvenciatartománybeli analízise az elõbbi módszerekkel szemben egyszerre hajtható végre (valójában a az amplitúdó - idõ és az amplitúdó - frekvencia leírását a waveletleírás két végletének tekinthetõ). Így a wavelet transzformáció segítségével egy éles változás a frekvenciaspektrumban annak elõfordulási idejével együtt, egyszerre határozható meg.

Egy wavelet a frekvencia-id? síkot (ez valójában a jel ``fázistere'') méretû cellára bontja. Ebben a térben a szokásos idõ- és frekvenciatartománybeli ábrázolás egy olyan speciális felbontásként fogható fel, amikor az adott cella egyik irányban végtelen kiterjedésû lesz (pontosabban lefedi a teljes megfigyelt spektrumtartományt ill. az egész megfigyelési idõt).

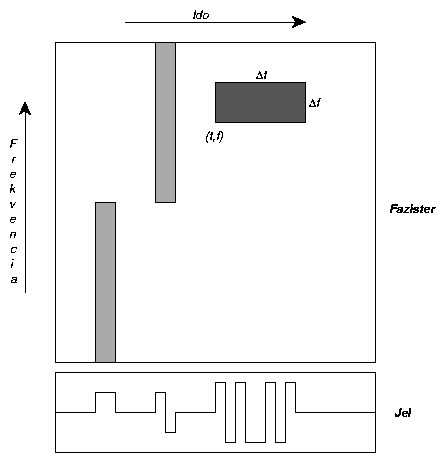
56. Ábra: Egy adott jelre jellemzõ területek a frekvencia-idõ síkon

Természetesen a fázissíkon végtelen számú felbontással kísérletezhetünk. A waveleteket ezek közül az emeli ki, hogy miközben frekvenciájuk viszonylag jól meghatározott, eközben idõbeli (térbeli) helyzetük is korlátozott. Ez a két feltétel - a kvantummechanikai határozatlansági relációhoz hasonló elvi okok miatt - nem elégíthetõ ki tetszõleges pontossággal egyszerre.

A jeleket ún. ortogonális bázisfüggvények szerint fejthetjük ki. Ha ezek a Dirac-delta függvények, akkot a szokásos amplitúdó-id? leíráshoz jutunk, ha ezek a sin és cos függvények, akkor ez a Fourier leírás. Az 57 ábrán e két leírás mellett más lehetséges wavelet bázisok néhány alapfüggvényét tüntettük fel.

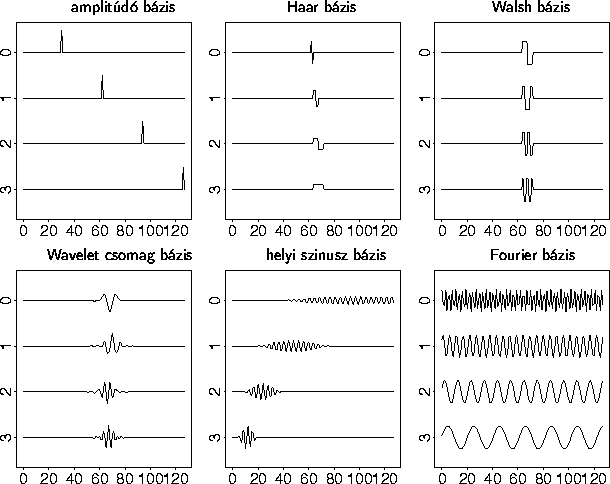
57. Ábra: Különbözõ, jelek leírására használható bázisfüggvények alakja. Az ábrákon a 0, 1, 2, 3 jellel jelölve a (0,128) idõintervallumban választható függvények különbözõ tagjai láthatóak: az amplitúdó bázis a szokásos amplitúdó-idõ leírást jelenti (ennek bázisfüggvényei a Dirac-delták). A Haar bázis az un. Haar függvényekbõl, a Walsh bázis a . oldalon említett Walsh függvényekbõl áll. A wavelet csomag bázis a 16.1 fejezetben tárgyalt DAUB4 függvényeket használja, a helyi szinusz bázis alapja egy adott frekvenciájú, de idõben Gauss-függvénnyel korlátozott idej? szinuszjel csomag. A Fourier bázist különbözõ amplitúdójú szinusz- és koszinuszfüggvények alkotják.

A wavelet transzformációk alapstruktúrája rekurzív szûrésekbõl és (az FFT CT algoritmusánál is megismert) páros-páratlan tagok szétválogatásából áll. A waveletek viszonylag alacsony (az FFT-vel összemérhetõ) számítási kapacitást igényelnek. A diszkrét wavelet transzformáció (DWT) az FFT-hez hasonlóan egy olyan gyors, lineáris szorzási mûvelet, amely a méretû bemen? vektort (adatsort) egy ugyanilyen méretû kimeneti vektorba transzformál át (FFT esetén ezzel a 12 fejezetben foglalkoztunk). Ezért mind az FFT, mind a DWT egy forgatásnak fogható fel az amplitúdó-idõ doménból a frekvencia-idõ térbe, és mindkettõ egy-egy mátrix segítségével is megadható.

Követklezõ: 16.1 A Daubechies waveletek Fel: Digitális jelek feldolgozása Elõzõ: Egyéb eljárásokmódszerek