Következõ: Tömörítési eljárások Fel: Wavelet transzformáció Elõzõ A Diszkrét Wavelet Transzformáció
![]()
![]()
![]()
Következõ: Tömörítési
eljárások Fel: Wavelet
transzformáció Elõzõ A
Diszkrét Wavelet Transzformáció
A DWT transzformációval most már megkísérelhetjük végrehajtani a fejezet elején említett fázistér vizsgálatot. A 60 ábrán néhány exponenciális lefutású, különbözõ amplitúdójú impulzust transzformálunk a wavelet térbe. Figyejük meg, hogy a fázistérben az egyes impulzusok környékén széles (pontosabban magas) frekvenciaspektrum jelenik meg! Ha a wavelet komponensek közül csupán az 512/32 legnagyobbat hagyjuk meg (szürke sáv), akkor ezek alapján majdnem tökéletesen megkaphatjuk az eredeti jelet.
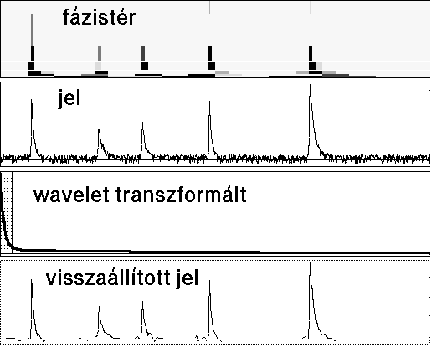
60. Ábra: Impulzusok DAUB4 wavelet transzformációja.
A visszaállított jel csak a szürkével jelölt
komponenseket használja. A wavelet komponensek nagyság szerint
csökkenõ sorrendbe vannak rendezve!
Ezzel az eljárás segítségével (ugyan veszteségesen de) tömöríthetjük a jelet. Természetesen itt nem csak az amplitúdót, hanem az adott wavelet pozícióját is el kell tárolnunk: így a fenti impulzusokat 1/16-od részére tömörítetük. Bebizonyítható, hogy az összes ortonormált bázis közül a wavelet segítségével érhetõ el a Shannon entrópia szerint mért legrövidebb együttes leírása az adatoknak és a modellnek (azaz a bázisfüggvényeknek). A wavelet rosszul tömöríti a jelhez kevert véletlen zajt: ennek eredményeképpen a csak a jelentõs wavelet komponensekbõl visszaállított jel esetén megjavítjuk a jel/zaj viszonyt is!
A wavelet tömörítés általában nagyon jól alkalmazható képek esetén. Szemünk különösen érzékeny az élekre, a wavelet transzformált pedig pontosan ezeket a változásokat tudja jól leírni, így elegendõ kevesebb paraméter rögzítése. A 61 ábrán egy kép és annak wavelet transzformáltja látható az elsõ DAUB4 lépés után. A transzformált képben a bal felsõ kép az x-y irányú simítás után létrejött kép, mellete van a csak vízszintes irányú, alatta a függõlegesé, a jobb alsó képen pedig a mindkét irányú ``durvítás'' eredménye.
A DAUB4 lépéseket a DWT-nek megfelelõen folytathatjuk, de érdemes megnézni az egy lépésben simított képbõl visszaállított képet a 62 ábrán. A visszaállított kép mellett látható az eredeti és rekonstruált kép különbsége is (a különbség kevesebb, mint a maximális amplitúdó 1%-a). Figyeljük meg, hogy a különbség az élek mellett a legnagyobb, a háttérben lévõ szikla majdnem tökéletesen rekonstruálható!