Következõ: Wavelet közelítések Fel: Wavelet transzformáció Elõzõ 16.1 A Daubechies waveletek

A Diszkrét Wavelet Transzformáció

A Diszkrét Wavelet Transzformáció (DWT) az elõzõekben megismert wavelet mátrix egymás utáni hierarchikus alkalmazását jelenti: elõször a teljes hosszúságú adatsorra alkalmazzuk, ezután a ``simított'' adatokat kivesszük, és ezt az N/2 adatsort szorozzuk be a mátrixszal, majd a ``simított-simított'' adatokkal ismételjük meg a mûveletet, s.í.t. . Az eljárást egészen addig folytatjuk, amíg csak két komponens nem marad:

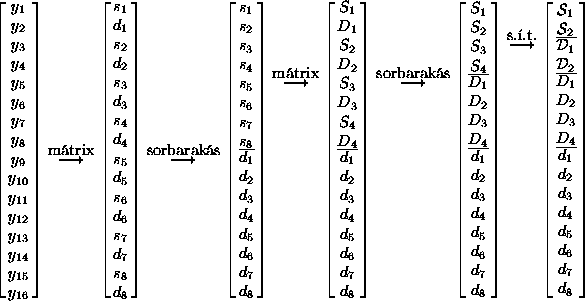
Láthatóan a transzormáció pont esetén két -el és a , D, d stb. wavelet együtthatók sokaságával ér véget. Mivel az egész eljárás ortogonális transzformációk sorozata, az DWT maga is ortogonális lineáris mûvelet. Az inverze egyszerûen az egész eljárás megfordításából áll (természetesen a wavelet mátrix helyett annak transzponáltját (azaz inverzét) kell használni).

A fenti algoritmus nagymértékben hasonlít az FFT CT algoritmusára: az egyes DWT mátrixszorzásoknak a lepkemûvelet alkalmazása feleltethetõ meg, míg a simított adatok kiválogatása az FFT rendezésével hozható párhuzamban. Különbség viszont, hogy az FFT esetén minden lépésben ponton végzünk mûveletet, míg a DWT esetén az adatok száma lépésenként felezõdik: ez jeleníti meg a DWT esetén az egyes frekvenciákhoz tartozó komponensek idõfüggését (l. 58 ábra).

A DWT segítségével a fázisteret hierarchikusan építjük fel, egymás után duplázva a frekvenciát és felezve a pontok számát (azaz duplázva a pontokra esõ idõintervallumok számát). A 58 ábrán látható módon az alacsony frekvenciák értékét viszonylag pontosan tudjuk, de elõfordulásuk idejét nem nagyon ismerjük. A magas frekvenciájú komponensek értéke rosszul (pontatlanul) ismert, de helyüket jól ismerjük.

  
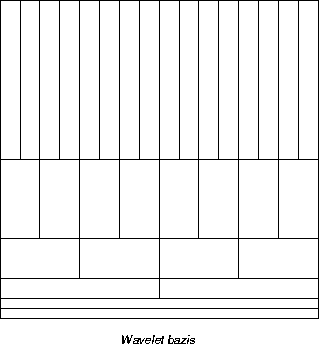
58. Ábra: A fázistér felosztása a DWT-vel.

Az inverz DWT segítségével kirajzoltathatjuk a DAUB4 waveleteket is. Az 59 ábrán a DAUB4 wavelet i=1, 10, 50 és 150 komponense látható N=512 pont esetén. Megfigyelhetõ, hogy i növekedésével a függvény egyre inkább egy keskeny intervallumra koncentrálódik, úgy, ahogy ezt a transzformáció hierarchikus felépítése alapján várjuk. A DAUB4 esetében a wavelet folytonos, de néhány pontban a jobboldali deriválja nem létezik!

  
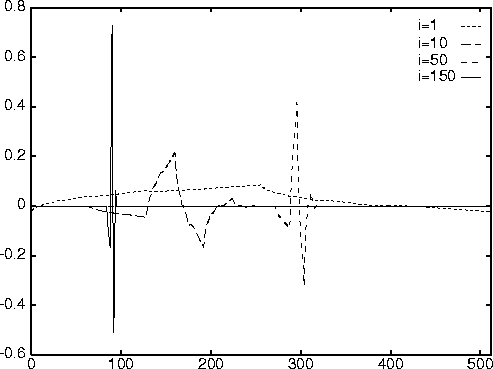
59. Ábra: A DAUB4 wavelet i=1, 10, 50 és 150 esetén 512 pontra. i=150 esetén a (128,255) intervallumban vagyunk, a wavelet az x=(150-128)/(256-128)*512=88 pont körül jelenik meg. i=50 esetén a (32,63) intervallumban vagyunk, a wavelet az x=(50-32)/(64-32)*512=288 pont körül jelenik meg. Kicsi i esetén a pozíciók pontatlanabbak (ui. a karakterisztikus frekvencia alacsony).

A DWT-t a Fourier-transzformációhoz hasonlóan n dimenzióban is elvégezhetjük: ilyenkor egyszerûen az dimenzió szerint sorban elvégzünk egy egydimenziós DWT-t.

Követklezõ: Wavelet közelítések Fel: Wavelet transzformáció Elõzõ: 16.1 A Daubechies waveletek