Következõ: Jelek vizsgálata zaj jelenlétében Fel: Digitális jelek feldolgozása Elõzõ Wavelet közelítések

Tömörítési eljárások

Az elektronikus eszközökkel létrehozott adatok (programok, képek, állományok) közül sok tartalmaz részben ismétlõdõ szakaszokat, részeket. Ezek az adatok általában különbözõ tömörítési algoritmusokkal (pl. a közismert pkzip vagy arj) eredeti méretük töredékére zsugoríthatók. Így csökkentõ az adatok átviteléhez szükséges idõ, redukálható a tárolásához szükséges hely. Az eljárások közül megkülönböztetünk veszteség nélküli és veszteséges eljárásokat (ez utóbbiak ugyan jobban tömörítenek, de az eredeti jelek tökéletes visszaállítása itt nem lehetséges).

A veszteségmentes tömörítõ eljárások közül legegyszerûbb a futási hossz kód. Ilyenkor pl. a 127 alatti karakterek jelzik, hogy hányszor kell az utánuk jövõ karaktert megismételni, a 128 feletti karakterek pedig a 128 feletti értékkel megadott számú, egymás után jövõ (különbözõ) karaktert jeleznek (hasonló eljárást használnak a faxokban is). Az eljárás ugyan egyszerû, de nem mindig hatásos: pl. egy ABABAB... szöveg esetén nem ismeri fel az ismétlõdõ mintát. Ilyen esetekre az ún. Lempel-Ziv-Welch eljárás tekinthetõ a módszer egyfajta kiterjesztésének: ekkor folyamatosan egy szótár épül fel sorban, dinamikusan a kódolandó adatokból. Minden egyes bejövõ adat (pl. byte) a korábbi adatokkal együtt egy új szót hoz létre. Ezt a szótár elemeivel összehasonlítjuk, és a maximális egyezésû szótárelem az új adattal együtt egy újabb szótárelemet hoz létre.

Nézzük a következõ példát! A szótárat a 63 ábrán láthatjuk, a kódolás pedig a 64 ábrán követhetõ nyomon. A bejövõ adatok balról jobbra kerülnek vizsgálatra. Az elsõ karakter a a. Mivel nincs hoszabb egyezõ szó a szótárban, ezért a ab szó bekerül a szótárba, 4-es kóddal.

  
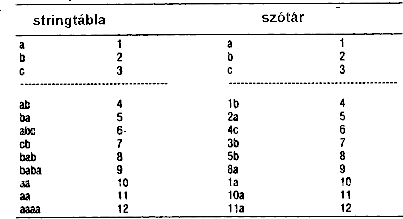
63. Ábra: Példa a szótár felépítésére az LZW eljárásban: a szótár a szaggatott vonal feletti három a, b, c karakterrel lett inicializálva.

A tömörített kódot a maximális egyezésû szótárelem pozíciója adja, a kimenetre csak az így megadott szótár-kód kerül.

  
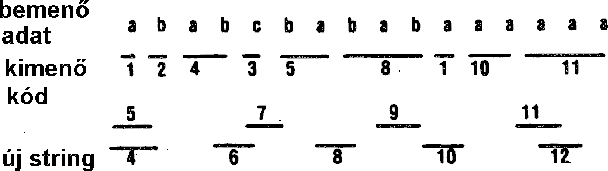
64. Ábra: Az LZW kódok elõállítása.

A szótár a méretét tipikusan - szóra választják. Amikor a szótár megtelik, akkor akkor azt letörlik (pl. byte méret esetén csak az elsõ 256 szó marad meg), majd újra indul az algoritmus.

A dekódoláshoz a bejövõ kódok alapján fel kell újra építeni a szótárat. Ez (a kódoláshoz hasonlóan) folyamatosan elvégezhetõ, azaz az eljárással az adatokat folyamatosan tömöríthetjük ill. állíthatjuk vissza. Több, adatfolyamban is használt program is (pl. gzip, compress) részben ezen az algoritmuson alapul.

Példánk dekódolását láthatjuk a 65 ábrán. Minden kód rekurzívan helyettesítõdik a prefix kódjával (szótárelem kódja) és a követ? karakterrel. A végeredmény az eredeti adatfolyam.

  
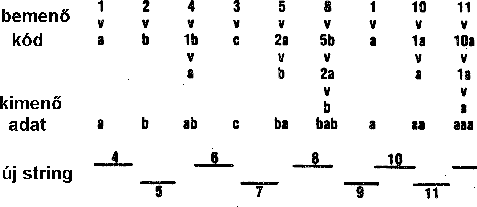
65. Ábra: Az LZW kódok dekódolása

Az eljárás hardware segítségével is könnyen megvalósítható (így valós idejû diszk tömörítés hozható létre!).

Bizonyos esetekben, amikor a bejövõ jelek eloszlása elõzetesen pontosan ismert, a fenti algoritmusoknál esetlegesen jobban tömörítõ ún. Huffman-kódolást is használhatunk. Ennek lényege a 66 ábrán látható: az eljárás az egyes jeleket (pl. karakterek) elõfordulásuk valószínûségében sorbarendezi. Ezek után a két legkisebb valószínûségû jelet helyettesíti egy olyan új jellel, amelynek valószínûsége a két jel valószínûségének összege. Ezután újra rendez, majd megismétli az egész folyamatot egészen addig, amíg csak két jel nem marad.

  
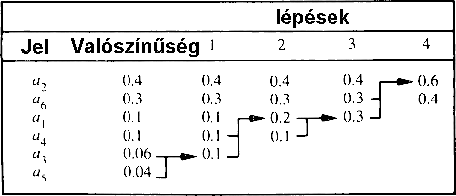
66. Ábra: A Huffman-kódolás rendezési lépései

A kódoláshoz megfordul a rendezési folyamat: pl. a nagyobb valószínûségû jelhez rendeljük a 0-t, míg az 1-et a kisebbhez. Ezek után visszalépünk egyet a rendezésben, és újra 0-t írunk a nagyobb, 1-et a kisebb jel kódja után (prefix kódolás). A visszalépéseket addig ismételjük, amíg minden elemi jelhez hozzá nem rendelünk egy kódot (l. 67 ábra). Az eljárás eredményeként a gyakran elõforduló jelek kódolása mindössze néhány bittel történik, míg eközben a nagyon ritka jelek akár 10-14 bites kódot is használhatnak. Érdekes megfigyelni, hogy az így elõálló kód egyértelmûen dekódolható, nem szükséges megjelölni az egyes kódok határait.

  
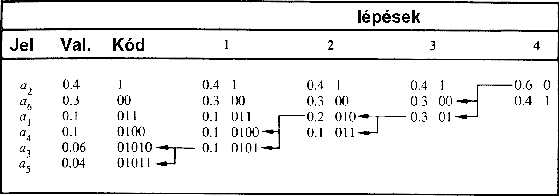
67. Ábra: A Huffman-kódolás kódolási lépései

Kérdés: Mekkora a példában szereplõ karaktersorozat és annak Huffman kódolásának Shannon-entrópiája?

Az eljárás ugyan jól tud tömöríteni, de hátránya, hogy a bejövõ jelek eloszlását ismerni kell (azaz folyamatos on-line tömörítést nem tudnk végezni vele). Ezen úgy segítenek, hogy megvizsgálják sok, hasonló jel eloszlását és ezek alapján felépítenek egy statikus kódtáblát (ennek használata gyorsabb, mivel nem kell elvégezni a rendezõ-kódoló lépéseket). Statikus kódtábla esetén ráadásul nem kell esetrõl-esetre rögzíteni (vagy a kommunikációs vonalon átküldeni) a kódtáblát.

A veszteséges kódolásokra példát láttunk a wavelet transzformáció során. A korszerû képtömörítési eljárások hasonló technikákat alkalmaznak, itt most az egyik leggyakrabban használt JPEG baseline coding eljárást nézzük meg:

A JPEG kódolást hosszú kutatómunka és kísérletezés elõzte meg. Az kódolási eljárás 8 bitre korlátozza a be és kimenõ adatok pontosságát. A képet elõször pixel méretû négyzetekre bontják, eltolják az egyenszintet a skála közepére, majd diszkrét koszinusz transzformációval (DCT) transzformálják és 11 bit pontossággal kvantálják. A DCT a bejövõ -es mátrixot a kövekezõképpen transzformálja:

A DCT komponenseket a -as négyzet sarkából cikk-cakk mintában haladva egydimenziós sorozattá alakítják (l. 68 ábra).

  
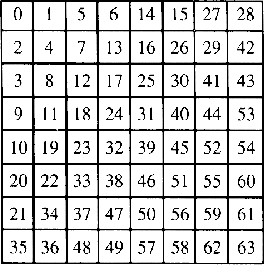
68. Ábra: A DCT komponensek sorbarendezése

Mivel így a DCT transzformált növekvõ frekvenciájú komponensei egymás mellé kerülnek, a homogén, egyszínû felületek sok egymás utáni 0-át tartalmaznak, ezért az AC komponenseket futási hossz kóddal tömörítik. A DC együtthatók viszonylag lassan változnak, ezért ezeknél csak a korábbi értékekhez viszonyított eltérést adják meg (delta kódolás). A szabvány megad elõre rögzített Huffman-kódokat is a kromacitás és luminancia színinformációk egyszerû, de hatékony kódolására is (de saját Huffman-kódtáblát is lehet használni). A JPEG veszteségének mértéke állítható: nagyobb pontossághoz nagyobb fileméret tartozik. Mivel az eljárás jól alkalmazkodik a gyakran elõforduló sima felületekhez, ezért pl. egy 1:25 arányban összenyomott JPEG kép általában még élvezhetõ minõségû. Az eljárás a pixelekból álló négyzetek miatt lokálisan adaptív, azaz képes alkalmazkodni az élekhez is: itt ugyan több DCT komponenst kell megõrizni, de általában viszonylag kevés ilyen (-as) blokk akad egy képen.

Követklezõ: Jelek vizsgálata zaj jelenlétében Fel: Digitális jelek feldolgozása Elõzõ: Wavelet közelítések