Következõ: FFT - Fast Fourier Transformation Fel: Digitális jelek feldolgozása Elõzõ Egy különleges alkalmazási példa

DFT - diszkrét Fourier transzformáció

 

A digitális számítógépek elterjedése a Fourier transzformáción alapuló eljárások csodálatos virágzását eredményezte. A digitális számítógépek azonban csak diszkrét értékekkel képesek dolgozni, ezért az ún. diszkrét Fourier transzformáció lehetõségei részletesebb vizsgálatot igényelnek.

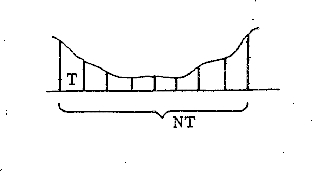
Ha egy folyamatos, sávlimitált jelbõl N számú mintát veszünk, akkor e minták alapján végrehajtott Fourier transzformáció (az általános képletnek idõben diszkrét értékekre való átalakításával) az alábbi lesz:

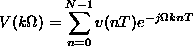ahol

A fenti képlet burkoltan, de határozottan arra utal, hogy a transzformáció a jelet N mintánként periódikusnak tekinti. Erre a felhasználások bizonyos fajtáinál érdemes ügyelni.

A diszkrét transzformációval kapcsolatban joggal vetõdik fel az a kérdés, hogy N mérési eredménybõl hány különbözõ k spektrumvonalat lehet meghatározni. Ha feltesszük, hogy és r=egész, akkor



vagyis a spektrum N értékenként teljesen megismétlõdik.- Továbbmenve: a 49 ábra mutatja, hogyan alakulhatnak a mintavételi törvényt figyelembe véve a valós és képzetes spektrumvonalak. Jól látható, hogy mind a szinuszos mind a koszinuszos komponenesek egy-egy szakaszon belül kétszer fordulnak elõ ugyanakkora értékkel. Természetesen a komponensek páros, illetve páratlan természetének megfelelõ elõjellel. Így azt állíthatjuk, hogy N adatból valójában csak N/2 független spektrumvonal meghatározására van mód. (A diszkrét transzformáció ezen tulajdonsága igen jól látszik a DSPLAY program használatánál.)

  
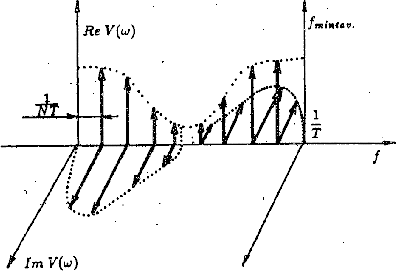
49. Ábra: A valós és képzetes spektrumvonalak alakja.

A diszkrét Fourier transzformáció - a képlet átrendezésével - értelmezhetõ mátrix mûveletként is, az alábbiak szerint []: 

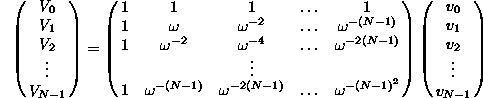
Érdemes észrevenni, hogy N=4 esetén a transzformáció igen egyszerûen végezhetõ el: érdemi szorzási mûvelet nélkül juthatunk el az eredményhez:

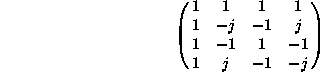
Azt is felfedezhetjük, hogy egy olyan mintavett jelsorozatnak, amelynek csak a kezdõ értéke nem zérus - vagyis egyetlen Dirac delta függvénybõl áll, - a diszkrét Fourier transzformáljának minden komponense azonos értékû.

A Fourier oda-- és visszatranszformáció természetszerûleg összefügg egymással. Az alábbiakban a két eljárás egymást követõ elvégzésével visszakaphatjuk az eredeti számsort. Figyeljünk arra, hogy az oda- és visszatranszformáció során csak egy 1/N faktor híján kapjuk vissza kiinduló értékeinket.

Követklezõ: FFT - Fast Fourier Transformation Fel: Digitális jelek feldolgozása Elõzõ: Egy különleges alkalmazási példa