Következõ: Az FFT gyakorlati alkalmazása Fel: Digitális jelek feldolgozása Elõzõ DFT - diszkrét Fourier transzformáció
Következõ: Az
FFT gyakorlati alkalmazása Fel: Digitális
jelek feldolgozása Elõzõ DFT
- diszkrét Fourier transzformáció
A Fourier transzformáció igen fontos eszköz jelek vizsgálatában, mérési eredmények értékelésében, stb. Nem kell tehát különösebben csodálkoznunk azon, hogy rengeteg munkát fordítottak a transzformáció részleteinek alapos kidolgozására.
A digitális számítógépek, valamint
a digitális méréstechnika elterjedése újabb
lökést adott a Fourier transzformáció alkalmazásának.
A digitális számítógépek azonban lényegüket
tekintve nagyon lomha, lusta rendszerek, mivel az aritmetikai mûveleteket
mindig logikai alapmûveletekre vezetik vissza. Külünösen
vontatottak a szorzások végzésében. A Fourier
transzformáció pedig igen sok szorzást igényel:
a mátrix koncepcióból eléggé nyilvánvalóan
következik, hogy N szám transzformációjához
szorzás szükséges. Egy 1000 mérési pontot
tartalmazó adatsor DFT-je tehát egymillió szorzást
igényel, ami a jelenlegi (átlagos) gépsebességek
mellett több/sok másodperces mûveleti idõt igényel.
(Az összeadások idejét nem szokás külön
beszámítani, mivel ennek idõigénye a szorzásnak
legfeljebb tizede.)
A Fourier transzformáció számítási idejét az 1965-ben Cooley és Tukey (CT) amerikai matematikusok által kidolgozott algoritmus csökkentette radikálisan. 1978-ban pedig Winograd lépett elõ egy új eljárással. Nézzük csak az alábbi összehasonlító táblát:
| szorzás/pont | összeadás/pont |
A CT - Fast Fourier Transmormation alapgondolata eléggé
kézenfekvõ: N pont DFT-je
szorzást igényel. Ha az adatokat két egyforma részre
bontjuk, akkor a két rész külön-külön
transzformációja 
szorzásba kerül. Ha a két transzformáció
részeredményei könnyen összekombinálhatók,
akkor érdemes ezt az utat választani. Az is nyilvánvaló,
hogy N-et célszerû 2 egész kitevõjû
hatványának választani, hogy a szorzás-spórolás
jótéteményébõl többszörösen
részesedhessünk.
A 50 ábrán az eredeti v
adatsorból a párosakat és páratlanokat szétválogatva
g és h adatsorokhoz juthatunk. A DFT képletének
mindkét adatsorra való alkalmazásával arra
az eredményre jutunk, hogy a G és H részspektrumok
összekombinálásához csak 
-nal
történõ szorzás kell, tehát viszonylag
olcsón "ússzuk meg" azt, hogy a két részre
bontással mûveleteket spóroltunk.
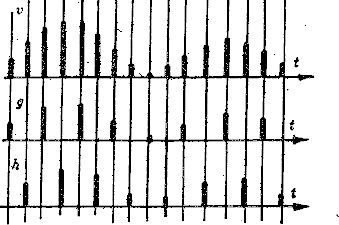
50. Ábra: Az adatsor szétválasztása
páros és páratlan sorokra.
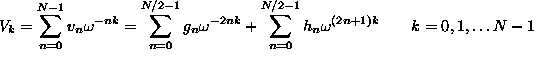
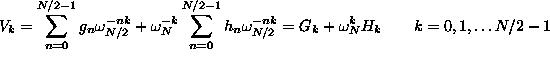
Ha k>N/2-1-nél, akkor k-N/2-vel helyettesíthetõ, így végül
A 51 ábrán az elõbbi elv alkalmazását ábrázoljuk grafikusan. Az ábra a./ részén feltüntettük a kiinduló adatokat, két csoportba szétválogatva. Az elõbb tárgyalt algoritmus szerint a V spektrumkomponenseket úgy kapjuk meg, ha két-két adaton az ún. lepkemûveletet végezzük el. (A ``lepke'' az ábra e./ részén látható: az A és B mennyiségeket alakítja át a megadott módon.) -- Természetesen meggondolásunk négy, illetve két adatra is érvényes (lásd a b./ ábra felsõ és alsó része).
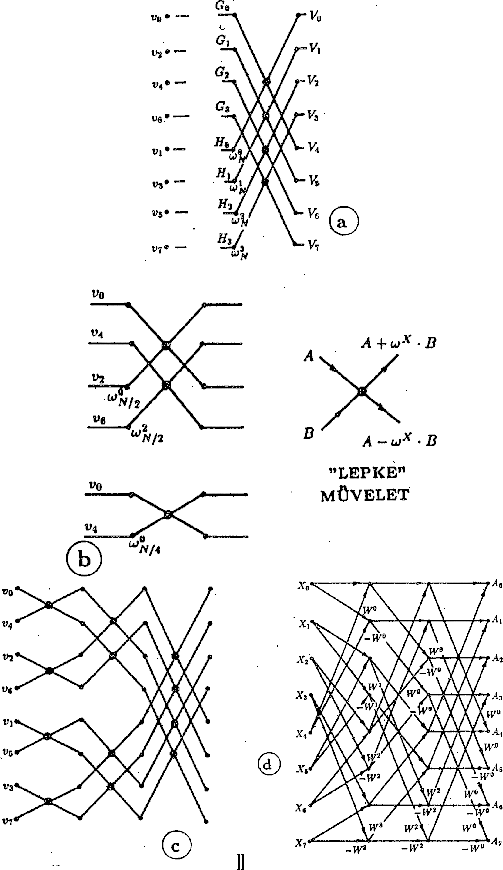
51. Ábra: Az FFT algoritmus részei N=8 esetén
Az ábra figyelmes vizsgálata arra a megállapításra
vezet, hogy a teljes transzformációhoz 
lepkemûvelet szükségeltetik (kettes alapú logaritmus).
Ha észrevesszük, hogy a lepkemûvelet tulajdonképpen
csak egyetlen -- de komplex -- szorzást tartalmaz, akkor az 
összefüggés a teljes FFT szorzás-igényét
adja meg. N=1024 esetén egymillió szorzás helyett
csak 10000 szorzást kell elvégezni, vagyis a DFT-hez képest
az FFT csak századannyi gépidõt használ.
Vegyük észre, hogy az FFT alkalmazásánál a bemenõ adatok nem sorrendben követik egymást, hanem furcsa módon meg vannak "keverve". A kiinduló adatok megfelelõ sorrendbe állítása is igényel némi gépidõt. Ennek elvégzéséhez is találtak ügyes eljárást. Figyelmes matemetikusok észrevették, hogyha 256 bemenõ adattal dolgoznak, akkor pl. a 158-ik adat helyére a 21-ik adat kerül. Ez az egy-egy értelmû leképezés az ún. ``bit-reverzálás'' nevû algoritmuson alapul, mely lényegében a biteknek a felezõ tengely körüli elforgatásából áll (l. 52 ábra).
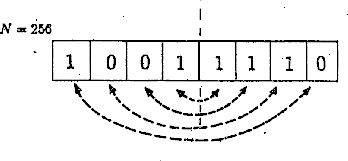
52. Ábra: A bit-reverzálás mûvelet
Felezési elven nagyon sokfajta FFT algoritmus létezik. A 51.c ábra szerinti eljárás nagy érdeme, hogy a számítások során nem igényel külön tárolóhelyet: a bemenõ adatok helyére íródhatnak a részeredmények, illetve a végeredmény. -- A 51.d ábra szerinti algoritmus viszont nem igényli a kezdõ adatok keverését, de a lepkemûvelete összetettebb, stb.
Befejezésül megadjuk az FFT-nek egy program listáját, BASIC nyelven. Az A tömbben a valós, a B tömbben a képzetes részeket tároljuk. A program két részbõl áll: az elsõ részben az adatok ``keverése'' történik, a második rész az igazi transzformáció.
DIM A(256), B(256)
NP=256 : ND=NP/2 : M=8 (
)
REM KEVERES
J=1
FOR I=1 TO NP-1
IF I<J THEN TR=A(I) : IT=B(I) : A(I)=A(J)
: B(I)=B(J) : A(J)=TR : B(J)=IT
K=ND
440 IF K<J THEN J=J-K : K=INT(K/2) : GOTO 440
J=J+K
NEXT I
REM TRANSZFORMACIO
LE=1
FOR L=1 TO M
LD=LE : LE=LE+LE
UR=1 : UI=0 : AN=3.1415926/LD
WR=COS(AN) : WI=-SIN(AN)
FOR J=1 TO LD
FOR I=J TO NP STEP LE
IP=I+LD
TR = A(IP)*UR-B(IP)*UI : IT=A(IP)*UI+B(IP)UR
A(IP)=A(I)-TR : B(IP)=B(I)-IT : A(I)=A(I)+TR : B(I)=B(I)+IT
NEXT I
TR=UR*WR-UI*WI : UI=UR*WI+UI*WR : UR=TR
NEXT J
NEXT L
A program begépelési hibamentessége könnyen ellenõrizhetõ: válasszunk egy tetszõleges bemenõ adatsort, transzformáljuk, a valós és képzetes részeket egyaránt osszuk el N-nel, fordítsuk meg a képzetes részek elõjelét, használjuk mégegyszer ugyanezt a programot és eredményül az eredeti adatsorhoz kell jutnunk.
Az FFT belsõ szerkezetének megértése sok esetben vezethet számítástechnikai elõnyhöz, vagyis kisebb futási idõhöz. Ha például azonos méretû szakaszokat kell egymás után folyamatosan transzformálni, akkor jobban járunk, ha két adatsort töltünk be a transzformáció indításakor, az egyiket a valós, amásikat a képzetes részbe. A transzformáció lineáris volta miatt ugyanis a két részspektrum az eredõbõl és annak konjugáltjából egy gyors/olcsó mûvelettel megkapható:
