Következõ: Egyéb eljárásokmódszerek Fel: Digitális jelek feldolgozása Elõzõ FFT - Fast Fourier Transformation

Az FFT gyakorlati alkalmazása

Az FFT igen hatékony számítási algoritmusa következtében szinte univerzális eljárássá vált. Igyekeznek mindenfajta feladatot úgy megfogalmazni, hogy az FFT-re visszavezethetõ legyen. Tipikus példa a konvolúció lehet: ritkán végzik ezt közvetlenül, az eredeti integrál-formula alapján. Inkább a frekvenciatartományú szorzást és az inverz Fourier transzformáció útját választják.

Az FFT, vagy annak valamely módosított változatának alkalmazásánál bizonyos tipikus kérdések szoktak felmerülni. Ezek között a legelsõ a szükséges gépidõ mennyisége. Gondoljuk végig, hogy milyen módszerek állnak rendelkezésre a számítások gyorsításához:

• gyorsabb számítógép, nagyobb órajel frekvenciával;
• aritmetikai processzor használata, esetleg gyors szorzó áramkörök alkalmazása;
• lehetõleg mindent számítsunk ki elõre, és ún. look-up table -bõl vegyük elõ a szükséges adatokat;
• ne számoljunk felesleges pontossággal, -- ha az AD konverter felbontóképessége csak 8 bit, ne használjunk 4O bites számábrázolást;
• keressünk minél hatékonyabb algoritmusokat, használjuk ki az az algoritmusok mélyén rejlõ lehetõségeket
• használjunk speciális elemeket, ún. DSP (digital signal processor) chipeket, amelyeket kifejezetten ilyen célokra terveztek és így igen gyorsak. Ezek tulajdonképpen speciális komputerek, nagyon gyors tárolóval, párhuzamos mûveleti egységekkel, a számítástechnika korszerû megoldásainak arzenáljával felszerelve.

A felsorolt javaslatok megvalósításának zöme elsõsorban pénzkérdés. Aki gazdagabb, gyorsabban transzformál.

A gyakorlati alkalmazások másik fontos témaköre ahhoz a tényhez kötõdik, hogy a DFT/FFT a transzformált szakaszt periódikusan ismétlõdõnek tekinti. Ennek következtében a kezdeti és befejezõ ``ugrások'' olyan nagyfrekvenciás komponensek forrásai, amelyek végeredményben a kapott spektrum meghamisítását, eltorzítását okozzák. Ezért elterjedt gyakorlat szerint a mintavett adatok transzformálandó szakaszát egy ún. ablakfüggvénnyel megszorozzák és a transzformációt csak ezután hajtják végre. Ezek az ablakfüggvények általában olyanok, hogy a szakaszhatárokon értékük zérus. Igy ugyanis kiküszöbölhetõk az említett nagyfrekvenciás zavarok. - Az ablakfüggvény léte azonban újabb torzítás kiindulópontja. Nagyon érdekes kérdés, hogyan kell tehát ezeket ez ablakfüggvényeket megválasztani.

Az 53 ábra a legrosszabb ablakfüggvény, a négyszögimpulzus esetét mutatja be (vagyis semmiféle adatkorrekciót sem végzünk).

  
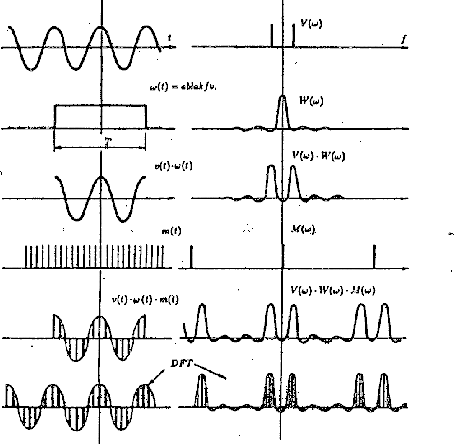
53. Ábra: A DFT energiaspektrum alakja négyszögimpulzus ablakfüggvény esetén

Az ábra bal oldalán azt követhetjük nyomon, miként jelölünk ki egy T szélességû ablakkal egy szakaszt a v(t) jelbõl. Ez a v(t) szinuszos, frekvenciaspektrumaként két vonalat várunk. A transzformált jelsorozat a bemenõjelnek egy négyszögjellel, valamint periodikus delta-függvénysorozattal történõ szorzásából áll elõ, -- az idõtartománybeli szorzásoknak frekvenciatartománybeli konvoluciók felelnek meg. -- A DFT elvégzése az adatok periodikus kiterjesztését jelenti, mintha T idõnként megismétlõdnének a minta diszkrét értékei.

Az ábra jobb oldalán a frekvenciatartományban látjuk ugyanezt. Feltûnõ, hogy az eredetileg vonalas az ablakjel hatására kiszélesedik és a végeredményül kapható spektrum is viseli az ablakfüggvény emlékét. A spektrum a DFT következtében csak vonalas lehet!

Ablakfüggvényként olyan jelalakokat választanak, amelyek a kezdõ és befejezõ szakaszokat csak igen kis súllyal veszik figyelembe. Ezek az ablakfüggvények számos szempont alapján értékelhetõk. Az alábbi táblázatban (54 ábra) feltüntettük a fõhullám szélességét, valamint az ún. hullámosságot. Ez utóbbi az elsõ mellékhullám és a fõhullám amplitudójának hányadosa. (E fogalmak eléggé triviálisak, ha a függvény alakjára gondolunk.)

  
54. Ábra: Különbözõ ablakfüggvények hatása a frekvenciatatományban

Követklezõ: Egyéb eljárásokmódszerek Fel: Digitális jelek feldolgozása Elõzõ: FFT - Fast Fourier Transformation