Következõ: Wavelet transzformáció Fel: Digitális jelek feldolgozása Elõzõ Az FFT gyakorlati alkalmazása
Következõ: Wavelet
transzformáció Fel: Digitális
jelek feldolgozása Elõzõ Az
FFT gyakorlati alkalmazása
Az FFT ismertetett változata mellett más hatékony algoritmusok is léteznek, amelyek spektrumok számítását, vagy ezzel közel ekvivalens értékû mûveletek végrehajtását segítik.
Léteznek például ún. gyors konvolúciós eljárások, amelyeket elsõsorban gyors jeldetektálási (jelfelismerési) feladványoknál használnak. Alapgondolatuk: a szorzások számának csökkentése, a feladat megoldásának érdekében az összeadások számának árán. Egy ilyen eljárás az ún. Strassen algoritmus. Az ötlet szinte kézenfekvõ: két komplex szám szorzatát a triviális négy szorzás és két összeadás helyett három szorzással és három összeadással is elvégezhetjük (Az (a-b)d szorzatot csak egyszer kell kiszámítani). Konvencionálisan:
A Strassen algoritmust elsõsorban az ún. cirkuláris
konvolució számítására használják.
(Ez végeredményben a konvolválandó jeleket
periodikusnak tekinti.) A konvolúciót három szakaszra
bontják, egy elõösszeadásra, szorzásra
és utóösszeadásra. Eléggé meghökkentõ
módon, egy 
-as
cikruláris konvoluciót a triviális 64 helyett 17 szorzással
is el lehet végezni. - Az elõbbi komplex szorzás az
algoritmus szerint tehát így néz ki:
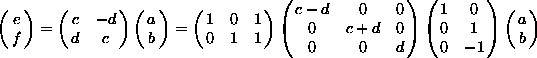
A Winograd féle gyors Fourier transzformáció hasonló
meggondolásokból indult. Ennél az eljárásnál
a részekre bontás primszámok, illetve ezek hatványai
szerint történik. Példaképpen bemutatjuk az 5
pontos Winograd transzformációt (
):
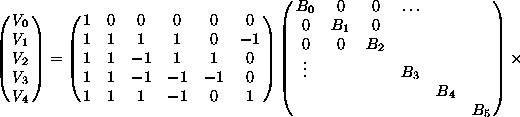
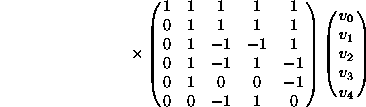
Bár a módszer az igényelt szorzások számának szempontjából nagyon hatékony, programozása nehézkes, memória-helyfoglalása nagyobb, mint a CT eljárás esetén lenne. Azt sem feledhetjük, hogy a bonyolult indexelés, a gyakori keresés a memóriában nem a sebességnövekedés irányába hat.
Itt említjük meg röviden, hogy létezik egy ún. Walsh transzformáció is, amelyet valaha a Fourier transzformáció komoly konkurensének tartottak. A Walsh függvények az ortogonális függvényrendszerek közé tartoznak, kétértékûek, elõállításukra egy rekurziós formula szolgál. A sin és cos függvények mintájára cal és sal függvényekrõl beszélhetünk. Jellegükrõl némi tájékoztatást a 55 ábráról kaphatunk. (A világos és sötét részek a kétérték? Walsh függvények mintájára változnak.)
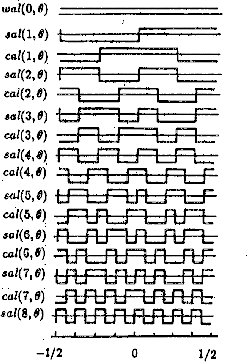
55. Ábra: A Walsh-bázis elsõ néhány
függvénye
A Walsh függvények tehát alkalmasak periodikus jelek komponensekre bontására. Valaha elõnyüket az jelentette, hogy e függvényeket egyszerû digitális áramkörökkel relatíve könnyen elõ lehetett állítani. Kétértékû voltukból következik, hogy a szorzás helyett csak öszeadni, kivonni kellett. Igy tehát megvalósítható volt a jelfeldolgozás nagy álma: az on-line (valós idejû) spektrum elõállítás. Sajnos, az örömbe némi üröm is vegyült, mert a Walsh függvényekre a konvolúció csak módosított formában érvényes. Az is hátrányos, hogy a ``természet'' lényegében nem ismeri ezeket a függvényeket, így szemléletes, vagy hasznos voltuk ugyancsak kérdéses. Ezek ellenére vannak bizonyos szakterületek, amelyek állítják, hogy jelfelismerési problémáikhoz a Walsh spektrumok igen jól használhatók.