Következõ: Kérdésekfeladatok Fel: Fourier sorokFourier transzformáció Elõzõ 2.2 Fourier sorok
Következõ: Kérdésekfeladatok
Fel: Fourier
sorokFourier transzformáció Elõzõ
2.2 Fourier
sorok
Nemperiodikus, impulzusszerû jeleket is felbonthatunk komposensekre.
Ekkor azonban a különbözõ frekvenciájú
komponensek végtelenül közel kerülnek egymáshoz,
ezért a 
mennyiség fog számot adni arról, hogy a 
tartományban mekkora a komponensek átlagértéke.
(Vagyis 
ún. spektrális "sûrûség"-függvényt
kapunk a transzformáció eredményéül. Vegyük
észre, hogy ennek dimenziója nem egyezik meg 
dimenziójával !) A legfontosabb (oda-vissza transzformáló)
összefüggések:
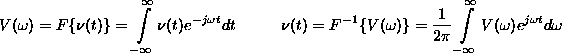
A Fourier transzformációnak több nagyon értékes tulajdonsága van, amelyeket a továbbiakban kihasználunk. Itt most ezeket fizikai szempontból röviden interpretáljuk.
|
|
a transzformáció lineáris (szuperpozíció) |
|
|
léptékváltoztatás. Rövidebb jelnek szélesebb a spektruma |
|
|
az idõeltolás nem változtatja meg a jel spektrumát |
|
|
a szinuszos moduláló jel eltolja a spektrumot, de alakját nem változtatja |
|
|
differenciálni a frekvenciatartományban igen egyszerû |
|
|
az integrálás is egyszerû |
|
|
a konvolúció a frekvencia-tartományban szorzássá redukálódik |
Megjegyzések
A frekvenciaspektrumot természetesen negatív frekvenciákra
is értelmezhetjük. A sin/cos függvények páros/páratlan
voltából adódóan ebbõl meglepõen
új információhoz azonban nem jutunk. A továbbiakban
frekvenciaspektrumon, - ha mást nem mondunk róluk, - a komponensek
abszolút értékébõl elõállított
ábrát értünk. Sokszor említjük az
energia-, illetve teljesítmény spektrumot is: itt a komponensek
négyzetét vesszük figyelembe. Ezekre a különbségekre
mindig ügyelnünk kell. A Fourier transzformáció
alaptulajdonságai következtében sok olyan eljárás
létezik, amelyek a spektrum elõállítását
megkönnyítik. Az 5 ábrán
egy szimmetrikus exponenciális görbe látható,
amelynek meg kell határoznunk a frekvenciaspektrumát. - Természetesen
mód lenne a transzformációs képletekbe behelyettesíteni,
de most más utat választunk. Ha a 
függvényt egymás után kétszer differenciáljuk,
visszakapjuk az eredeti függvény alakját, meg egy ideális
impulzust (Dirac deltát). - A kétszeri differenciálás
négyzetével való szorzást jelent. Ennek segítségével
az eredeti függvény frekvenciaspektrumára vonatkozó
összefüggés könnyen felírható, - amibõl
közvetlenül kifejezhetõ. (Az ideális impulzusnak
a frekvenciaspektrumáról az 
részben találunk ismereteket.) Figyeljünk fel arra,
hogy az exponenciális, valamint a sin/cos függvények
kétszeri deriválás után ugyanazt az alakot
adják (csak az Y skála lesz más). A fenti eljárás
tehát célszerûen alkalmazható, ha a megnevezett
függvények, vagy azok szakaszai szerepelnek az eredeti idõfüggvényben.
A Fourier transzformáció általában sokat egyszerûsödik, ha észrevesszük, hogy a függvény páros, vagy páratlan-e, illetve ha tudatosítjuk, hogy a függvény milyen szakaszok összegébõl áll elõ. Ha ezek a szakaszok könnyen transzformálhatók, akkor csak az eltolt függvények miatti komplex mennyiséget kell az egyes spektrumkomponensek összeadásánál figyelembe venni. - Az is sokat használ, ha rájövünk arra, hogy a transzformálandó függvény egy kétértékû (0 és 1 ) függvénynek és egy könnyen transzformálható függvénynek a szorzata. - Mindezekre számos példát találunk a Feladatok c. jegyzetben.
