Következõ: Kérdésekfeladatok Fel: Fourier sorokFourier transzformáció Elõzõ Kérdésekfeladatok

Négyszögjel frekvenciaspektruma

Viszonylag részletesen foglalkozunk egy egyszerû, periodikus jelalakkal, a négyszögjellel. Az 6 ábrán ún. szimmetrikus négyszögjelet ábrázoltunk, a koordinátarendszer origójához képest eltolt helyzetekben. A periodikus négyszögjel frekvenciaspektruma viszonylag könnyen meghatározható, csak az erre rendelt képletet kell használnunk. Azt is tudjuk elõre, hogy a spektrum "vonalas" lesz, vagyis csak diszkrét frekvenciákhoz tartozó eredményeket várhatunk. - Az eredmények vizsgálata sok értékes, általánosítható ismerethez vezet.

Elõször azt a szimmetrikus jelet választjuk, amelyik az origóhoz képest szimmetrikusan helyezkedik el. Ez páros függvény, így csak koszinuszos komponenseket kaphatunk.

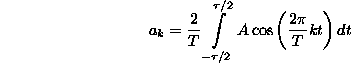
a számolást elvégezve a következõ - célszerûen átrendezett - eredményre jutunk:

( A a négyszögjel amplitúdója, , k pedig egész, - mutatja, hogy hányadik felharmonikusról van szó.) Az 1.3.1. ábrán mutatjuk esetében a felharmonikusokból létrehozott frekvenciaspektrumot.

  
6. Ábra

Fel kell hívnunk a figyelmet a következõkre:

1. a spektrumvonalak burkológörbéje sin(x)/x függvény szerinti. Ez a függvény rendszeresen, újra és újra fel fog bukkanni;
2. a spektrumvonalak 1/k szerint csökkenõ értékûek;
3. a szimmetrikus négyszögjelbõl a páros harmonikusok hiányoznak, csak a páratlanok zérustól eltérõ értékûek;
4. értéke zérusra adódik, mivel a négyszöghullámot éppen így helyeztük el. Vegyük észre, hogy a négyszögjel függõleges helyzetének változása csak az ún. egyenáramú középértéket befolyásolja, a felharmonikusok nagyságát nem !

Ismételjük meg vizsgálatunkat a esetre. Az eredmény az 7 ábrán látható.

  
7. Ábra

Itt a következõk érdemelnek figyelmet:

1. a burkológörbe most is - triviálisan - szerinti;
2. a spekrtrumvonalak amplitúdója az elõzõ esetben tapasztalt értékek 1/5 -ére csökkent, mivel is ilyen arányban változott;
3. a burkológörbe elsõ zérushelyéig n spektrumvonalat találunk. n meghatározható a összefüggésbõl. spektrumkomponenst találunk az elsõ zérushelyig;
4. az elsõ néhány spektrumvonal lényegében azonos amplitúdójú.

Fogalmazzuk meg általános tapasztalatként: ha T állandó és csökken, a spektrum kiszélesedik. Ha állandó és T növekszik, akkor az alapharmonikusok frekvenciája csökken, a spektrumvonalak sûrûsödnek. A spektrumkomponensek amplitúdója mindkét esetben csökken.

Követklezõ: Kérdésekfeladatok Fel: Fourier sorokFourier transzformáció Elõzõ: Kérdésekfeladatok