Következõ: Összefüggés az autokorrelációs függvény és az Fel: Véletlenszerû jelek autokorrelációs függvényei Elõzõ Példa

Példa

 

  
27. Ábra

Az 27 ábrán ún. "véletlen távírójelet'' látunk. Ez úgy áll elõ, hogy Poisson eloszlás szabja meg azokat az idõpillanatokat, amelyikekben az egyébként bináris függvény értékei változnak. (A Poisson eloszlásról a valószínûségszámítás tárgyban lehet bõvebben tanulni. Itt csak annyit jegyzünk meg, hogy a radioaktív bomlások idõbeni statisztikáját ez az eloszlás írja le. - Az elõzõ esethez képest az most lényeges különbség, hogy itt az értékváltozások idõpillanatai véletlenszerûek, nem periodikusak.) A Poisson statisztika szerint annak a valószínûsége, hogy idõtartam alatt éppen k esemény következik be () az események közötti "átlagos" idõtartam):

Az autokorrelációs függvény:

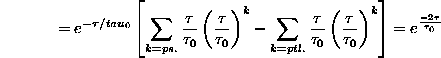
Észre kell vennünk, hogy a szögletes zárójelben lévõ sorozat éppen egy exponenciális függvény Taylor sora. Mivel az autokorrelációs függvény páros, a végeredmény :

Sikerült tehát ennek a véletlenszerûen viselkedõ függvénynek is zárt formában megkapni az autokorrelációs függvényét.