Következõ: Összefoglalás Fel: Korrelációs függvények Elõzõ Példa

Összefüggés az autokorrelációs függvény és az energiaspektrum között

Mind elméleti, mind gyakorlati szempontból igen fontos az alábbi transzformációs pár, amelyeket Wiener tételnek is neveznek:
 

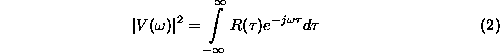
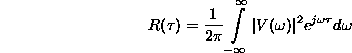
Az autokorrelációs függvény és a jel energiaspektruma között tehát kapcsolat van, egyik ismeretében a másik meghatározható. (A képleteket itt nem bizonyítjuk, de igazságuk eléggé könnyen átlátható, ha arra gondolunk, hogy az autokorrelációs függvényt úgy is megkaphatjuk, hogy egy v(t) jelet egy h(t) = v(-t) súlyfüggvényû hálózaton visszük keresztül. (Miért is?) A konvolúciót frekvenciatartományú szorzással helyettesítve közvetlenül jutunk az energiaspektrumhoz, vagyis a Wiener tétel felismeréséhez.) A képletek felhasználásával a fenti 6.2.1. és 6.2.2 példa véletlenszerû jeleinek is megkaphatjuk az energiaspektrumát. Az 28 ábrán ezek kvalitatív képét láthatjuk. Vegyük észre, hogy az 6.2.1 példa generálási folyamatában van periodicitás, ennek nyoma az energiaspektrumban is határozottan .megtalálható.

  
28. Ábra

(Nagyon jelentõs észrevétel: az autokorrelációs függvénybõl nem tudjuk az eredeti függvényt visszakapni, - valamifajta információveszteség történik. Természetesen az energiaspektrumból sem lehet a jelet visszaállítani. Fontos azt is tudatosítani, hogy nagyon különbözõ jeleknek lehet azonos jellegû energiaspektrumuk: például az RC aluláteresztõ áramkörre adott ideális impulzus hatására keletkezõ kimenõjelnek és ugyanezen hálózaton a sávlimitálás nélküli fehér zaj hatására létrejövõ kimenõjelnek az energiaspektruma megegyezik.)