Következõ: Kérdésekfeladatok Fel: Lineáris rendszerek jellemzõi és vizsgálatuk Elõzõ Kérdésekfeladatok
Következõ: Kérdésekfeladatok
Fel: Lineáris
rendszerek jellemzõi és vizsgálatuk Elõzõ
Kérdésekfeladatok
Az a furcsa kérdés, hogy mennyire hasonlít egy függvény önmagára, eléggé értelmetlennek tûnik. - Azt azonban könnyû átlátni, hogy egy függvény hasonlíthat idõben eltolt változatára. - Az 2.1 szakaszban már azt is láttuk, hogy a hasonlóság mértéke a két függvény szorzatának integráljával arányos.
Az autokorrelációs függvényt úgy állítjuk
elõ, hogy az eredeti függvényt és a 
értékkel eltolt függvényt összeszorozzuk
egymással. Eredményül az 
függvényhez érkezünk:
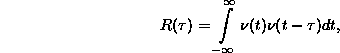
illetve:
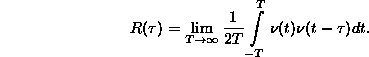
Az autokorrelációs függvény legfontosabb tulajdonságai könnyen átláthatók, illetve érthetõk:
:a függvény az origóra szimmetrikus. 
a 0 pontban felvett értéke a jel energiájával
arányos 
:maximális értéke a 0 pontban található
Az 21 ábrán egyszerû függvényeket és autokorrelogramjukat mutatjuk be. Néhány egyszerû összefüggést, szabályt könnyû átlátni. - Az impulzusszerû függvények autokorrelációs függvényei is impulzusszerûek. A periodikus jelek megõrzik periodicitásukat. A zajszerû jelek autokorrelogramja pedig impulzusszerû.
Érdemes arra is figyelni, hogy
Az autokorrelátorok, mint jelvizsgáló eszközök - a digitális számítógépek elterjedése elõtti idõkben - igen fontosak voltak. Sok szakma használta õket, különösen ott, ahol a jelek a hangfrekvenciás tartományba, vagy annak közelébe estek. Ez esetben ugyanis a jelek késleltetését a magnetofonfejek közötti távolság változtatásával egyszerûen meg lehetett oldani.
Autokorrelációs módszerrel elsõsorban zajjal fedett jeleket értékeltek. Az egyik sikeres alkalmazást a pulzárok felfedezése jelenti. Ez tulajdonképpen tipikus alkalmazásnak is számíthat, mert zajszerû jelben vadásztak valamifajta periodicitásra.
Az autokorrelációs függvényhez hasonlatosan
az ún. ``keresztkorrelációs függvény''
is definiálható, illetve értelmezhetõ:
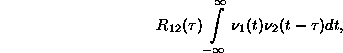
Nagyon érdekes eredményre jutunk, ha egy rendszer bemenõjele és kimenõjele közötti keresztkorrelációs függvényt állítjuk elõ (22. ábra)
Az alábbi meggondolások végeredménye nagyon
fontos: ha 
lényegesen rövidebb idõtartamú, mint h(t),
- vagyis a bemenõjel lényegében zajszerû és
autokorrelációs függvénye impulzusszerû
- akkor a mérõrendszer kimenetén a súlyfüggvényt
kapjuk eredményül. (Az impulzusfüggvénnyel való
konvolúció után ugyanis az eredeti függvényt
kapjuk vissza.)
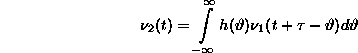
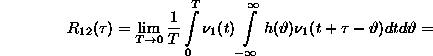
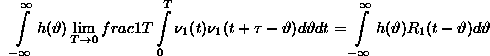
Így olyan eljárás birtokosai lettünk, mellyel egy rendszer súlyfüggvénye akár üzem közben is meghatározható, - a rendszer kis amplitúdójú zajjal történõ zavarásával. Ennek az elvnek a méréstechnikai értéke igen nagy (pl. nukleáris reaktoroknál).
