Következõ: Példa Fel: Korrelációs függvények Elõzõ Kérdésekfeladatok
Következõ: Példa
Fel: Korrelációs
függvények Elõzõ Kérdésekfeladatok
Stacionernek és ergodikusnak azokat a folyamatokat nevezzük,
amelyek statisztikus jellemzõi az idõben állandóak
és amelyek sok hasonló folyamat egyidejû vizsgálatával,
vagy egyetlen folyamat idõbeni elemzésével egyaránt
megkaphatók, vagyis az ún. idõátlag és
halmazátlag (sokaságátlag) azonos. 23
ábra ezt kívánja szemléletessé tenni:
mindegy, sok hasonló generátor 
jelét mérjük-e egyetlen to pillanatban, vagy egyetlen
zajgenerátor jelét vizsgáljuk igen hosszú idõn
keresztül.
A véletlenszerû folyamatok statisztikai adatokkal, statisztikai
függvényekkel írhatók le (átlagérték,
momentumok, stb). A továbbiakban kiemelkedõ szerepe lesz
az ún. sûrûség- függvényeknek. -
Tekintsünk egy véletlenszerû idõfüggvényt,
melynek pillanatnyi amplitúdója x(t) és
vegyünk belõle sokszor mintát. A mintavételek
idõpontját is véletlenszerûen - 
- válasszuk. (Ez bizonyos körülmények között
periodikus is lehet.) A p(x)dx értékkel
azt adjuk meg, hogy a jelbõl véletlenszerû idõpontban
mintát véve, mekkora valószínûséggel
találjuk a mért amplitúdó értéket
x és (x+dx) között. A 
kifejezés adja meg, hogy ha két mintavétel között
éppen 
nagyságú rögzített idõkülönbség
van, mi a valószínûsége, hogy az egyik mért
érték x és (x+dx) közé
esik, valamint a másik az y és (y+dy)
közötti amplitúdó tartományban lesz. (24.
ábra)
Ez utóbbi együttes valószínûség
értelmezéséhez tekintsük az 25
ábra szerinti mérõberendezést. Itt két
analóg-digitál átalakító
idõkülönbséggel ugyanabból a jelbõl
vesz mintát. A mért értékeket tároljuk
egy mátrix-szerû elrendezésben. Ez - szemléletesen
- egy négyzetes memória-blokk, amelyiknek minden elemében
egy számláló található. E számlálók
tartalma akkor növekszik eggyel, ha az AD konverterek mérési
eredményei éppen ezt a cellát jelölik ki, - a
mért x és y értékekkel. - (Ez
a mérési elrendezés a "mátrix analizátor"
nevet viseli, és elsõdlegesen két nukleáris
detektorról érkezõ különbözõ
amplitúdójú (energiájú) jelek kölcsönös
esemény- valószínûségének mérésére
szolgál.)
A bemenõjel a jelen esetben legyen 
határfrekvenciájú fehér zaj. Ezt a fogalmat
majd késõbb alaposabban is megismerjük, - itt csak annyit
kell tudnunk róla, hogy lényegében véletlenszerû
jel, amelyiknek a frekvenciaspektrumában egy meghatározott
értéknél nagyobb frekvenciák egyáltalán
nem fordulnak elõ.
-Ha
nagyon kicsi (a zaj ún. korrelációs idejéhez
képest), akkor x értékének ismeretében
eléggé jól meg lehet jósolni y mivel
a két érték valószínûleg alig
tér el egymástól. Ha
növekszik, a jóslás egyre bizonytalanabb lesz, nagy
idõkülönbségeknél pedig lehetetlen. A mérõberendezés
nyilván gyakoriságokat mér, amelyeket bizonyos szabályok
betartásával valószínûségekké
módosíthatunk. A 
függvényt tehát az elõbb ismertetett eszközzel
megmérhetjük. Bizonyos ismert mechanizmusú folyamatoknál
azonban matematikailag, analitikusan is meghatározhatjuk. Ennek
jelentõsége azért nagy, mert ennek ismeretében
az autokorrelációs függvényt is elõállíthatjuk.
Az autokorrelációs függvény az alábbi
formula alkalmazásával is megkapható:
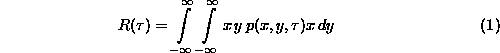
Ezt a képletet itt nem vezetjük le, csak értelmezzük,
illetve elfogadhatóvá tesszük. - Elsõként
gondoljuk meg, hogy a korreláció és a keresztkorreláció
képleténél mit is csináltunk.: minden
értéknél képeztük a függvényértékek
szorzatának összegét. Most is errõl van szó:
Az 
és 
értékek a függvényértékek egy-egy
sávját jelölik ki . Az integrálási határok
arra utalnak, hogy ezek értéke bármi lehet. A
értékkel azért kell megszoroznunk õket, hogy
az elõbbi definíció értelmében az együttes
elõfordulási valószínûségüket
is figyelembe vegyük. - Az elemi szorzatokat természetesen
összegezni is kell, - erre utal a kétszeres integrálás.
A továbbiakban két érdekes esetet fogunk megvizsgálni azért, hogy a fenti képlet hasznosságáról fogalmat alkothassunk.
