Következõ: Digitális szûrôk megvalósítása Fel: Digitális jelek feldolgozása Elõzõ Mintavételi törvény

z-transzformáció, digitális szûrôk

A mintavett jelek feldolgozási lehetôségeinek talán legfontosabb területe az, amit összefoglaló névvel digitális szûrônek neveznek. Kialakulását a digitális méréstechnika, valamint a komputerek elterjedése tette lehetôvé, illetve határozottan sürgette. Ez a módszer hardware és software elemekkel évrôl évre gyarapszik és alkalmazási területeinek korlátjai ma még nem látszanak. A matematikailag korrekt elmélet eléggé terjedelmes, esetenként nehéz. Mi itt nem ezt az utat követjük, hanem az elméleti eredményeket egyszerû példákon illusztráljuk és általános érvényûnek nyilvánítjuk.

A digitális szûrôt úgy tekintjük, mint egy eljárást, amely egy elemekbôl álló bemeneti számsorozatot számsorozattá transzformál. Ily módon tulajdonképpen általánosítjuk az eddig általunk használt egyszerû szûrô-fogalmat. - A digitális szûrô vázlata 38 ábrán látható: lényegében késleltetô elemekbôl áll, amelyek kimeneteit súlyfaktorokkal szorozva összegezzük. A késleltetô elemek mindegyike egy szám tárolására alkalmas, ezek tartalma - hurkatöltô módjára - egyszerre mozog, ahogy ezt már a shift-regiszterek esetén is láttuk. (Elektronika jegyzet, 115. o.) A számok mozgatását a teljes rendszerre hatásos "clock", vagy szinkronjel végzi, - ezt általában nem tüntetjük fel, ennek ellenére minden esetben a rendszerhez tartozónak tekintjük. A késleltetô lánc periodikusan is, de nem periodikusan is mozgatható.

Kézenfekvô, hogy a folyamatos jelek vizsgálatánál megszokott ideális impulzust (delta függvényt) , és annak hatására keletkezô súlyfüggvényt értelemszerûen diszkrét jelekre is alkalmazzuk. - A súlyfüggvényt most -nel jelöljük, ezt az ún. Kronecker-delta hatására kapjuk. A delta függvény egyetlen egyesbôl áll, ami elôtt és mögött zérusok állnak.

Nézzük végig figyelmesen az (3) táblázatot, amelybôl azt a fontos következtetést vonhatjuk le, hogy a bemeneti Kronecker deltából kimeneti számsort kapunk, melynek értékeit a - súlyfaktorok szabják meg. (Ebben a konkrét esetben a súlyfaktorok értékeit 3, 5, 7, 2, -3 értékûre választottuk.) Egy fontos felfedezést kell tennünk: ezzel a módszerrel akármilyen súlyfüggvényt is közelíthetünk, még olyanokat is, amelyek fizikai hálózatokkal nem hozhatók létre !
 

  
38. Ábra

E fogalom felhasználásával a diszkrét jelekre vonatkozó konvolúció az alábbiak szerinti:

Ennek értelmezéséhez vizsgáljunk egy példát részletesen (4 Táblázat). A súlyfaktorok (vagyis meghatározói) most legyenek 1, 3, 12, -11, -0.1; - a bemenô számsor pedig 1, 5, 13, 0, -6, -10. - A "történést", vagyis a számok áthaladását a 38 ábra szerinti eszközön könnyen áttekinthetjük. Az alábbi sémán ((4) táblázat) ezt látjuk:
 

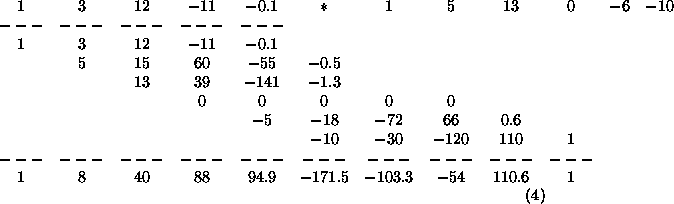
Az tûnik fel, hogy a konvolúció látszólag szorzás jellegû. Ez természetes is, mert az egyes bejövô értékek "egy helyértékkel - idôben(?) - eltolva" adódnak össze. A fenti "furcsa" szorzás eredménye arra utal, hogy polinom szorzást végeztünk.

Természetesen az elôbb megadott és számértékeket egy polinom együtthatóinak is tekinthetjük. A polinom változójának megadásában látszólag szabad kezünk van. Lehetne x egész kitevôjû hatványait is használni, azonban mi itt a késleltetés mértékére a egész számú hatványait fogjuk használni. Ennek oka az, hogy az ún. z-transzformáció tradicionális elnevezés és jelentôsége manapság rendkívül fontos. A negatív kitevôjû hatványok a transzformáció matematikáját jelentôsen egyszerûsítik. Igy tehát a fenti "szorzás" eredményét úgy is felírhatjuk, hogy:

A fentiekbôl azt látjuk, hogy a polinom szorzást és a z-transzformáció szerint kifejezett számértékek sorát közeli rokonság fûzi egybe. Az is fontos felfedezés, hogy a közönséges, elemi iskolában tanult szorzás és konvolúció között sok, lényegi összefüggés rejlik.

A bemenô számsort, a súlyfüggvényt, a kimeneti számsort kibôvíthetjük z megfelelô hatványaival. Az így keletkezô polinomokat z-transzformáltaknak nevezzük. Közöttük a következô - triviálisnak tûnô - összefüggés áll fenn:

A z-transzformáción alapuló digitális szûrôk 33 ábra szerinti típusát véges impulzusválaszú szûrônek nevezik (finite impulse response = FIR). Nyilvánvaló, hogy a súlyfüggvénynek csak annyi eleme lehet, ahány késleltetô elemet használunk.

  
39. Ábra

A FIR szûrôk mellett azonban léteznek IIR (infinite impulse response) szûrôk is. Ezek legegyszerûbb változata a 39 ábrán látható. Mûködését könnyen megérthetjük, ha azt gondoljuk, hogy bemenetére egy Kronecker delta érkezik. Ha , akkor a kimeneti számsor 1, 0.9, 0.81, stb lesz, - és ez a geometriai sor végtelen hosszú lehet (pontosabban: ez a sorozat is véges, mert a számítógép által kezelhetô legkisebb számig tarthat csak). Viszonylag könnyen, zárt formában is fel tudjuk írni a kimenô számsor z-transzformáltját (a geometriai sorokra vonatkozó összefüggések alapján):

Természetesen ez csak akkor konvergens, ha B/z < 1 . (Kicsit pontosabban: B semmiképpen nem lehet egynél nagyobb, mert 39 ábrán látható sémánk szerint ilyenkor a kimenet korlátlanul naggyá válik.) Az a következmény is eléggé meglepô, hogy itt végtelen hosszan tartó súlyfüggvényhez jutunk egyetlen késleltetô elem felhasználásával. Az elôbbi eredményt azonban másként is megkaphatjuk az ábra alapján:

A 39 ábra szerinti digitális szûrô tehát úgy viselkedik, mint egy kváziintegráló áramkör, - legalábbis a súlyfüggvényük lényegileg hasonló. Vajon hogyan lehetne kvázidifferenciáló jellegû digitális szûrôt csinálni? A 40 ábra ezt mutatja. Mivel a kvázidifferenciáló áramkör súlyfüggvénye egy delta függvénnyel kezdôdik, ezért az elôbb tárgyalt IIR szûrôt egy FIR szûrôvel egészítjük ki. - Az ábra mutatja a súlyfüggvényt, - ez éppen megfelelônek tûnik.

  
40. Ábra

Kiszámolhatjuk ennek z-transzformáltját is:

Érdekes módon a súlyfüggvény z-transzformáltját most egy törtfüggvény írja le. Ha és -et választunk, akkor a bemeneti Kronecker deltából éppen egy darab kimeneti jel származik. Ehhez kapcsolódik az IIR rész exponenciálisan csökkenô jele.

  
41. Ábra

A fentieket összefoglalva azt mondhatjuk, hogy a digitális szûrôk általános alakja a 41 ábra szerinti, a szûrô súlyfüggvénye pedig egy racionális törtfüggvény. A kimenô számsor részben a bemeneti, részben pedig a kimeneti számsorból alakul ki. Tudnunk kell azt is, hogy a 41 ábra (bal oldala) szerinti általános megoldásnál "tömörebb'' kevesebb késleltetô elemet használó sémák is léteznek. Erre példát a 42 ábra jobb oldalán látunk. - Egy általános z- transzformált az alábbi formában írható fel:

Érdemes észrevenni, hogy értéke csak egy lehet, továbbá k és m értékének nem kell megegyezniök.

A racionális törtfüggvények számos tulajdonságát használhatjuk ki, például azt, hogy a nevezôt rész-polinomok szorzataként is elôállíthatjuk, - így a transzformáció a komputerek számára egyszerûbb, gyorsabb lesz. (Pl. egy páros fokszámú polinomot másodfokú kifejezések szorzataként is realizálhatunk, - ahogy ez gyakorlatban sokszor meg is történik.)

A parciális törtekre bontás hasznosságára mutatunk egy példát. Az alábbi H(z) függvény "szelídnek" tûnik. Ha azonban megkeressük a nevezô gyökeit (ezek 2/3 illetve - 5/3 nagyságúak) és felírjuk a részlettörteket, akkor azonnal szembe tûnik, hogy az egyik tört nem lehet stabil.

Valóban, ha ezt a z-transzformációt a DSPLAY programba beírjuk, futtatásakor a program "elszáll", így adva tudtunkra, hogy H(z) -t rosszul választottuk meg. (A z-transzformáltak stabilitásának vizsgálata az alkalmazások nagyon lényeges része!)

Érdekes és tanulságos eredményhez jutunk, ha a 39 ábra szerinti "kváziintegráló" elrendezést kicsit más szemszögbôl vizsgáljuk. Képzeljük el, hogy eddigi, diszkrét idôpontokban történô léptetési feltételezéseink kibôvítéseként most a késleltetô elem valódi késleltetést nyújt. - Egy mûvonal darab, vagy üvegszálas kábel alkotja a késleltetôt, amelyek tehát folytonos (analóg) jeleket is késleltetnek. Ha a 39 ábrán látható kapcsolás bemenetére Dirac-deltát adunk, a kimeneti frekvenciakarakterisztika könnyen elôállítható. A késleltetésû rendszer impulzusátvitele ugyanis , vagyis az ábra szerinti kapcsolás amplitúdó átvitele:

Ez a karakterisztika szerint periodikus. Érdemes ezt az átviteli karakterisztikát az RC kváziintegráló kapcsolás átvitelével összehasonlítani. A két karakterisztika látható a 42 ábrán. Mindkét görbe kezdeti szakasza nagyjából hasonló, azonban az RC áramkör átvitele a frekvencia növekedtével monoton csökken, míg a késleltetôs áramköré ettôl lényegesen eltér. Figyeljünk fel arra, hogy ez a karakterisztika a periodikus mintavételi eljárás során keletkezô frekvencia-átvitellel lényegében megegyezik (32 ábra).

  
42. Ábra

Követklezõ: Digitális szûrôk megvalósítása Fel: Digitális jelek feldolgozása Elõzõ: Mintavételi törvény